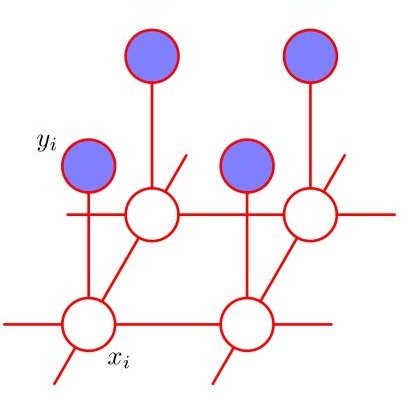
We introduce a Gibbs Markov random field for spatial data on Cartesian grids which is based on the generalized planar rotator (GPR) model. The GPR model generalizes the recently proposed modified planar rotator (MPR) model by including in the Hamiltonian additional terms that better capture realistic features of spatial data, such as smoothness, non-Gaussianity, and geometric anisotropy. In particular, the GPR model includes up to infinite number of higher-order harmonics with exponentially vanishing interaction strength, directional dependence of the bilinear interaction term between nearest grid neighbors, longer-distance neighbor interactions, and two types of an external bias field. Hence, in contrast with the single-parameter MPR model, the GPR model features five additional parameters: the number $n$ of higher-order terms and the parameter $\alpha$ controlling their decay rate, the exchange anisotropy parameter $J^{nn}$, the further-neighbor interaction coupling $J^{fn}$, and the external field (bias) parameters $K$ (or $K'$). We present numerical tests on various synthetic data which demonstrate the effects of the respective terms on the model's prediction performance and we discuss these results in connection with the data properties.
翻译:我们引入了Gibbs Markov 随机域域, 用于碳酸盐网格的空间数据, 这个域以通用的平板转转动器模型(GPR) 模型为基础。 GPR 模型将最近提议的修改的平板转动器模型(MPR) 模型(MPR) 概括化, 在汉密尔顿模型中增加更多术语, 更好地捕捉空间数据的现实性特征, 如光滑性、 非Gausianity 和几何反异质。 特别是, GPR 模型包含最多无限的更高级调和快速消失互动强度的波音调、 近邻电网邻居间双线互动期的方向依赖性、 长距离相邻互动和两种外部偏差字段的双线性能。 因此, GPR 模型包含五个额外参数, 与单参数 MPR 模型( $ 或 $K ) 相比, 更高级调价数和 控制其衰减率的参数( $ ), 交换 Antonopy 参数 $ $ $ $, $,, 和 外部外字段( 参数) 参数参数参数参数参数参数参数参数参数参数参数,, 我们用 和合成数据 讨论这些合成数据 和合成数据 数据 数据 数据 的对比 。