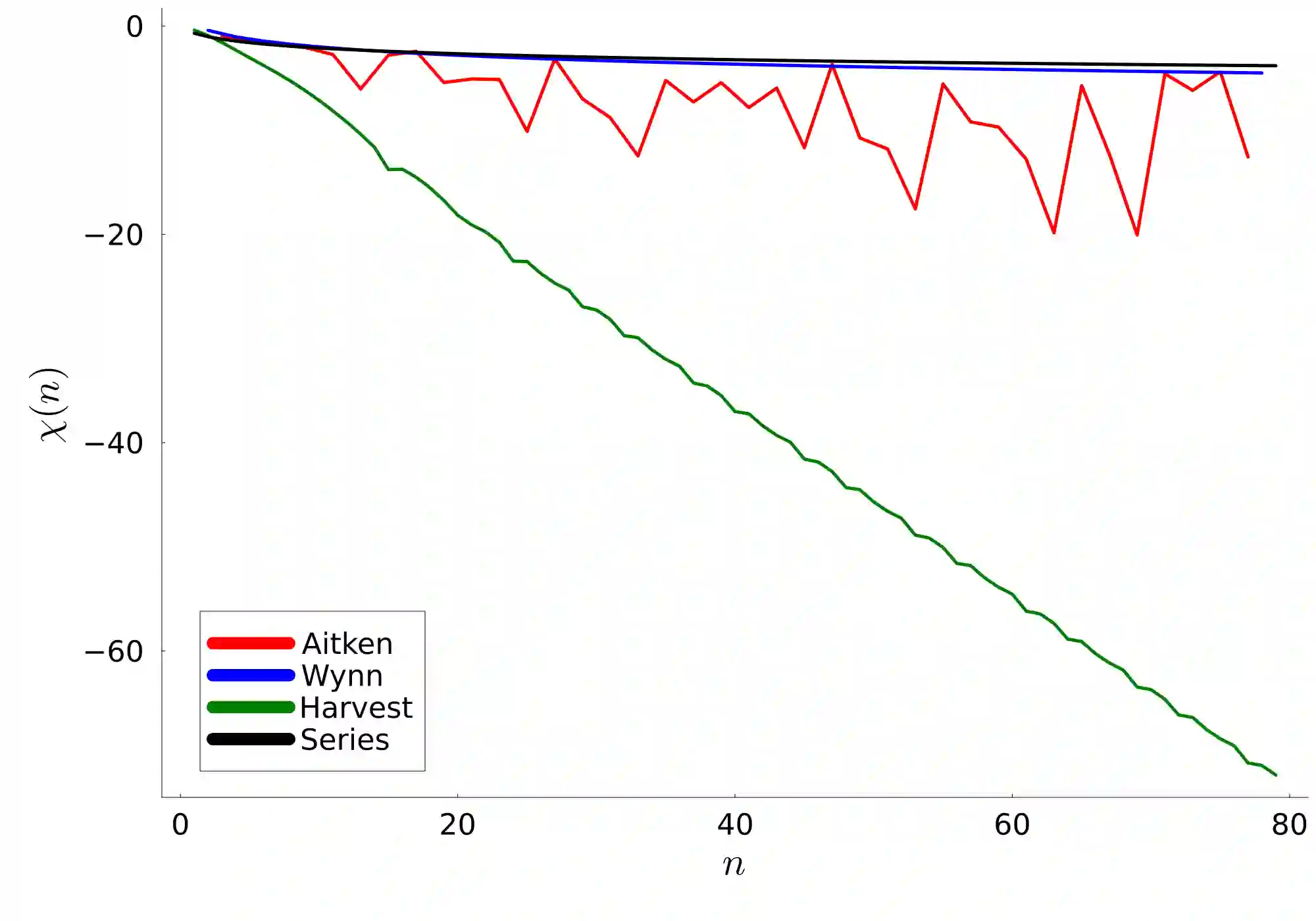
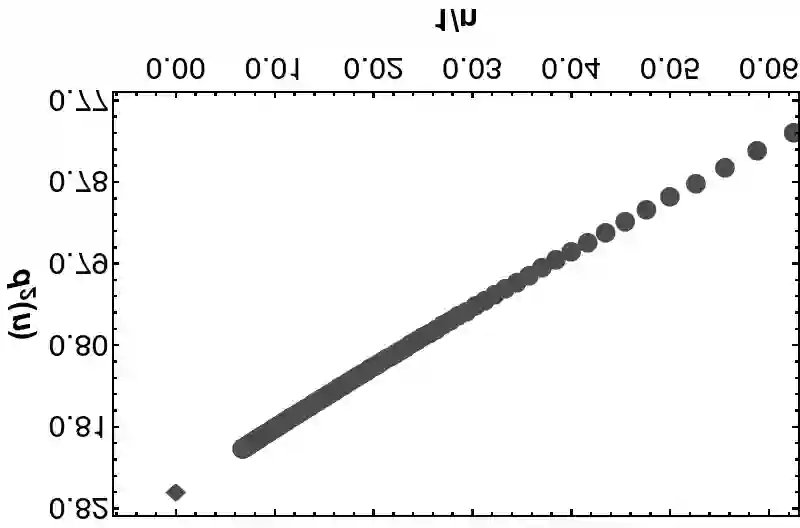
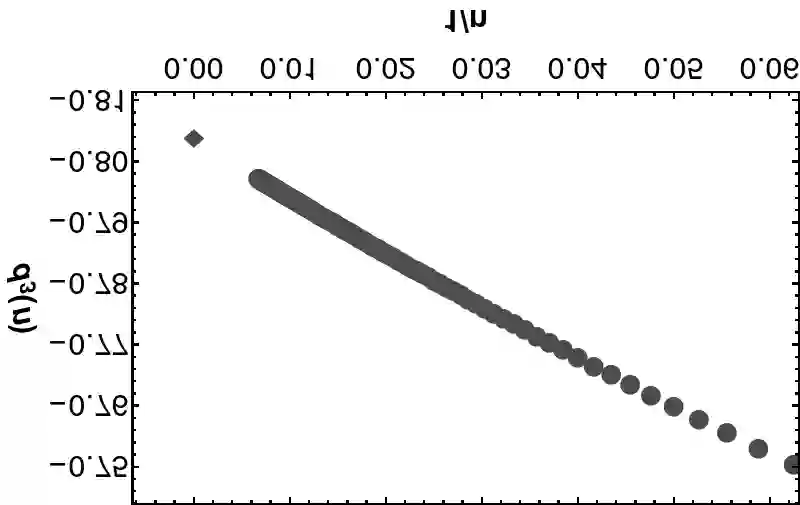
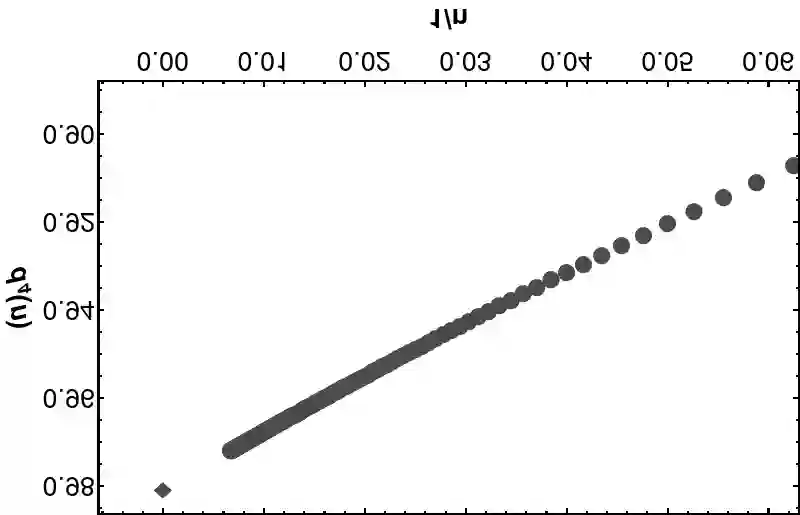
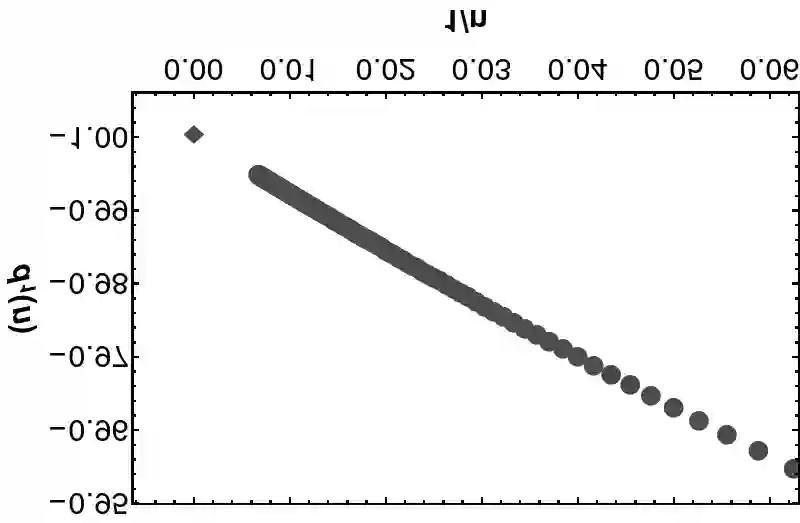
The recursive Neville algorithm allows one to calculate interpolating functions recursively. Upon a judicious choice of the abscissas used for the interpolation (and extrapolation), this algorithm leads to a method for convergence acceleration. For example, one can use the Neville algorithm in order to successively eliminate inverse powers of the upper limit of the summation from the partial sums of a given, slowly convergent input series. Here, we show that, for a particular choice of the abscissas used for the extrapolation, one can replace the recursive Neville scheme by a simple one-step transformation, while also obtaining access to subleading terms for the transformed series after convergence acceleration. The matrix-based, unified formulas allow one to estimate the rate of convergence of the partial sums of the input series to their limit. In particular, Bethe logarithms for hydrogen are calculated to 100 decimal digits.
翻译:暂无翻译