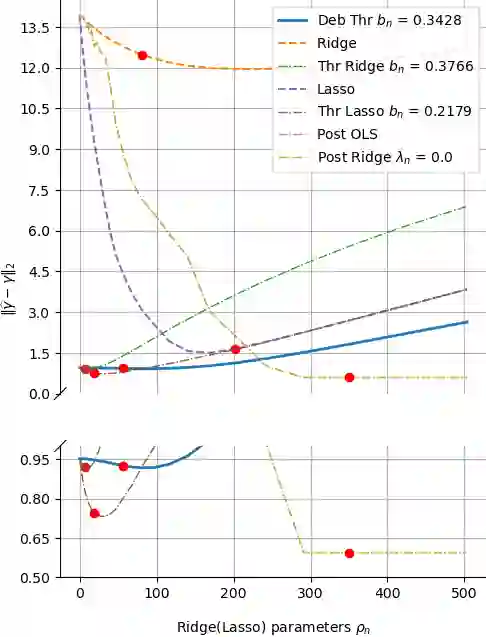
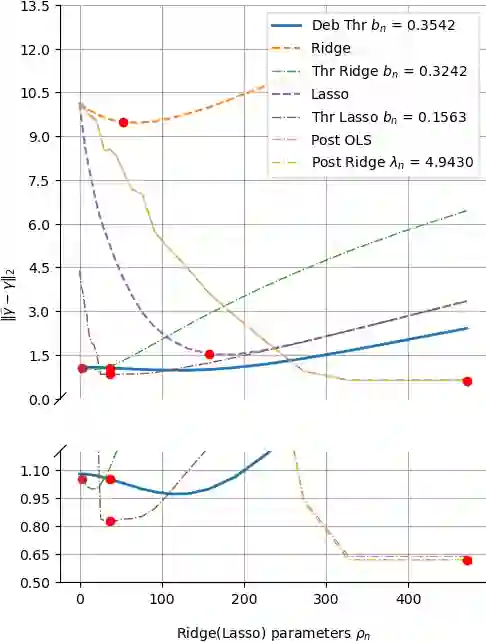
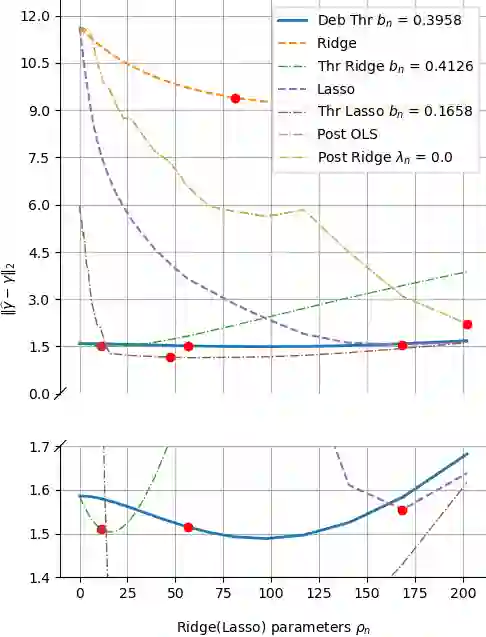
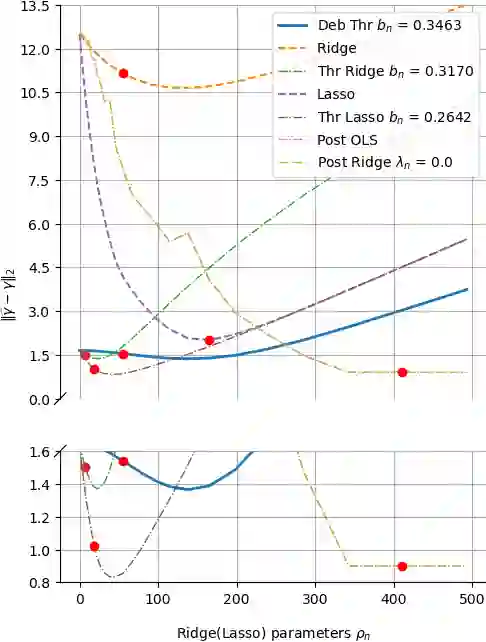
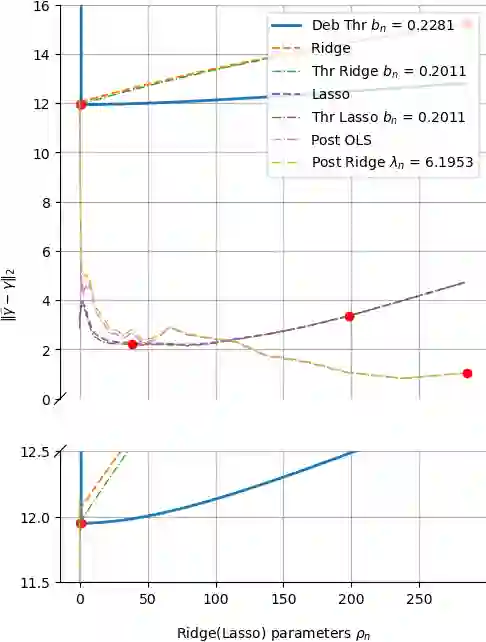
The success of the Lasso in the era of high-dimensional data can be attributed to its conducting an implicit model selection, i.e., zeroing out regression coefficients that are not significant. By contrast, classical ridge regression can not reveal a potential sparsity of parameters, and may also introduce a large bias under the high-dimensional setting. Nevertheless, recent work on the Lasso involves debiasing and thresholding, the latter in order to further enhance the model selection. As a consequence, ridge regression may be worth another look since -- after debiasing and thresholding -- it may offer some advantages over the Lasso, e.g., it can be easily computed using a closed-form expression. % and it has similar performance to threshold Lasso. In this paper, we define a debiased and thresholded ridge regression method, and prove a consistency result and a Gaussian approximation theorem. We further introduce a wild bootstrap algorithm to construct confidence regions and perform hypothesis testing for a linear combination of parameters. In addition to estimation, we consider the problem of prediction, and present a novel, hybrid bootstrap algorithm tailored for prediction intervals. Extensive numerical simulations further show that the debiased and thresholded ridge regression has favorable finite sample performance and may be preferable in some settings.
翻译:在高维数据时代,Lasso的成功可归因于它进行隐性模型选择,即零出不显著的回归系数。相比之下,古典山脊回归不能显示潜在的参数的宽度,也可能在高维环境下带来巨大的偏差。然而,最近关于Lasso的工作涉及贬低和阈值,后者是为了进一步加强模型选择。结果,山脊回归可能值得再做一次审视,因为 -- -- 在贬低和阈值之后 -- -- 它可能比Lasso具有一些优势,例如,它很容易使用封闭式表达法来计算。%,它具有与Lasso相似的性能。在本文中,我们定义了一种偏差和阈值的峰值回归法,证明了一个一致性结果,并用高尔斯近标来进一步强化模型选择。我们进一步引入了野生的测距算法,以构建信任区,并进行线性组合参数的假设测试。除了估算外,我们还考虑预测问题,并且提出一种新颖的、混合级靴带的回归率测算法,以精确度测测算,以显示某种可测量的精确度测算。