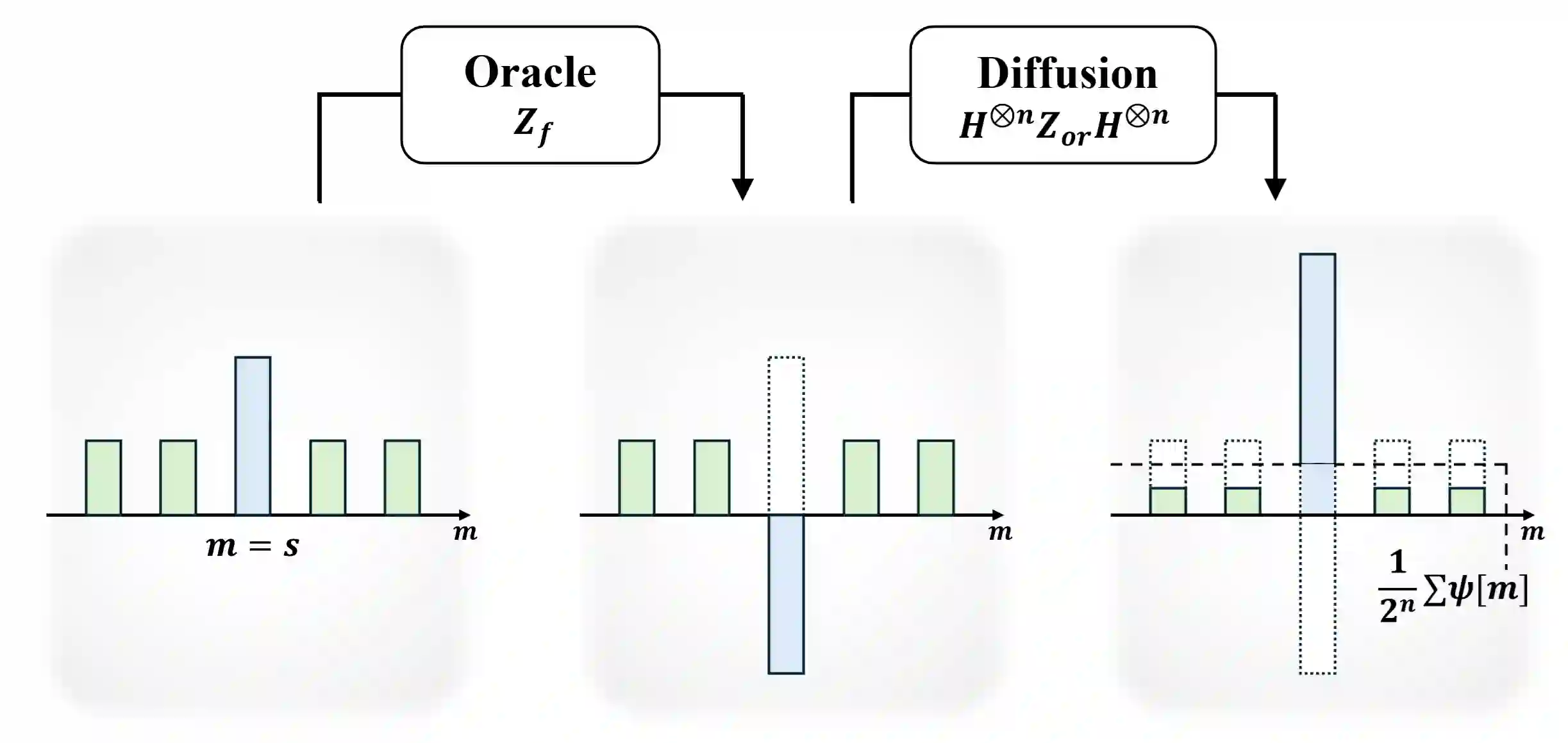
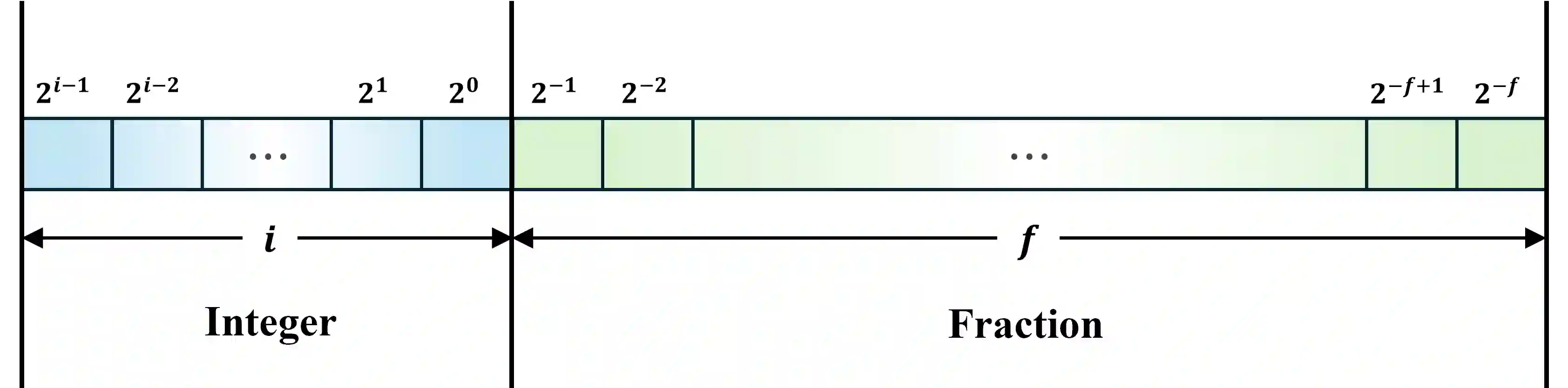
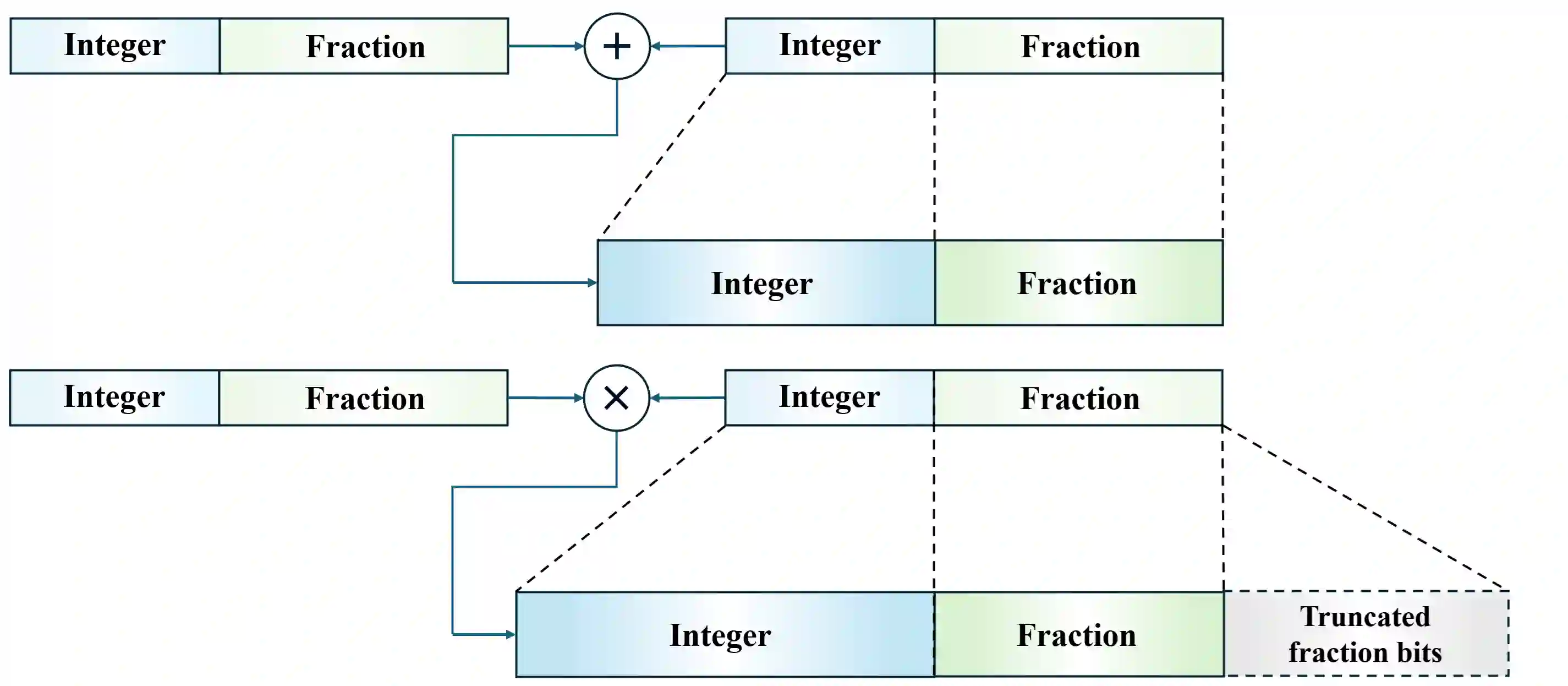
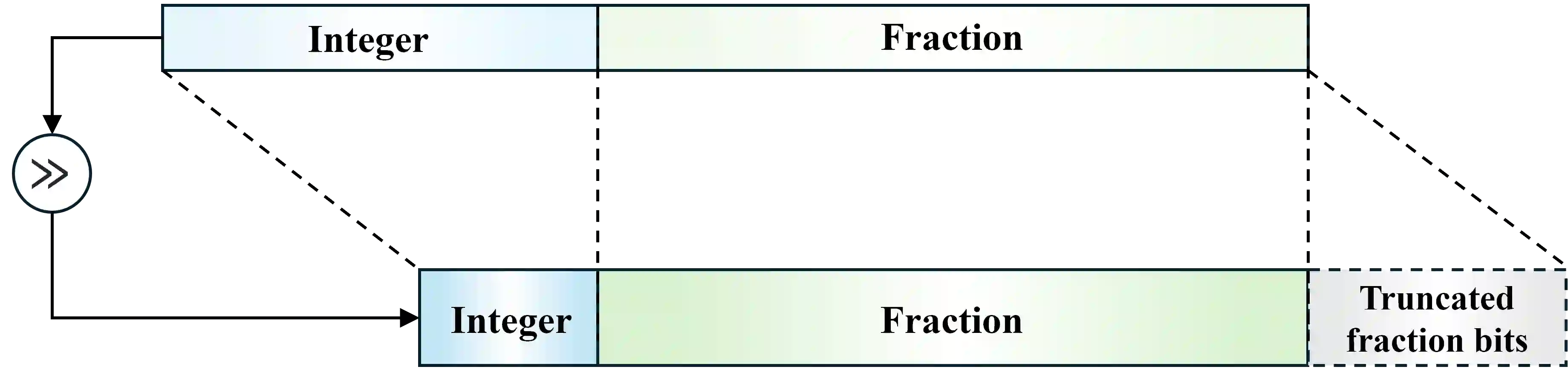
Quantum computing (QC) emulators, which simulate quantum algorithms on classical hardware, are indispensable platforms for testing quantum algorithms before scalable quantum computers become widely available. A critical challenge in QC emulation is managing numerical errors from finite arithmetic precision, especially truncation errors in resource-efficient fixed-point arithmetic. Despite its importance, systematic studies quantifying how truncation errors impact quantum algorithm accuracy are limited. In this paper, we propose a rigorous quantitative framework analyzing truncation error propagation in fixed-point QC emulation, focusing on Grover's quantum search algorithm. First, we introduce a simplified two-value amplitude representation of quantum states during Grover's iterations and prove its theoretical validity. Using this representation, we derive explicit mathematical expressions characterizing truncation error accumulation across quantum gate operations. We quantify the overall emulation error by the $\ell_2$ distance between ideal and emulated probability distributions, obtaining asymptotic bounds scaling as $O(2^{n-f})$, where $n$ is the number of qubits and $f$ is fractional-bit precision. Extensive numerical simulations and empirical experiments on a practical fixed-point QC emulator confirm that observed errors precisely match our theoretical predictions. Finally, we provide a closed-form formula to determine the minimal fractional-bit precision required to achieve a specified error threshold, offering clear guidelines for emulator designers balancing accuracy and resource utilization.
翻译:暂无翻译