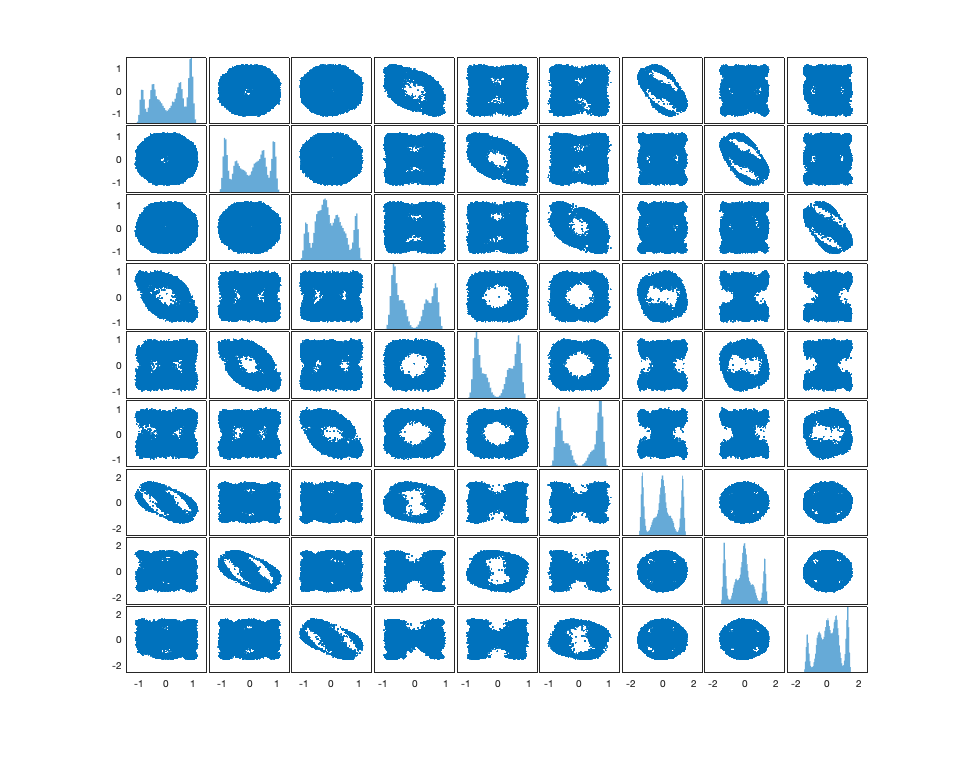
We introduce a novel geometry-informed irreversible perturbation that accelerates convergence of the Langevin algorithm for Bayesian computation. It is well documented that there exist perturbations to the Langevin dynamics that preserve its invariant measure while accelerating its convergence. Irreversible perturbations and reversible perturbations (such as Riemannian manifold Langevin dynamics (RMLD)) have separately been shown to improve the performance of Langevin samplers. We consider these two perturbations simultaneously by presenting a novel form of irreversible perturbation for RMLD that is informed by the underlying geometry. Through numerical examples, we show that this new irreversible perturbation can improve estimation performance over irreversible perturbations that do not take the geometry into account. Moreover we demonstrate that irreversible perturbations generally can be implemented in conjunction with the stochastic gradient version of the Langevin algorithm. Lastly, while continuous-time irreversible perturbations cannot impair the performance of a Langevin estimator, the situation can sometimes be more complicated when discretization is considered. To this end, we describe a discrete-time example in which irreversibility increases both the bias and variance of the resulting estimator.
翻译:我们引入了一种新的、基于几何学的不可逆扰动,加速了Bayesian计算Langevin算法的趋同。我们清楚地证明,Langevin的动态存在扰动,在加速其趋同的同时保持其惯性测量。不可逆扰动和可逆扰动(如Riemannian extroulent Langevin 动态(RMLD))被分别显示为改善Langevin算法的性能。我们认为,这两种扰动同时加快了Langevin测算法的趋同。我们同时提出一种基于基本几何测算法的RMLDD不可逆扰动新形式。我们通过数字实例表明,这种新的不可逆扰动性扰动动态可以改善对不可逆转扰动性测量的性能的预测,而没有考虑到这些干扰。此外,我们还表明,不可逆性扰动性扰动通常可以与Langevin算法的Stochatic梯度版本一起实施。最后,虽然连续时间不可逆扰动性扰动不会损害Langev 估测算师的性性,但当考虑离性变性的变化有时会更加复杂,但当考虑离性的变化在考虑离性变化中产生这种差异时会增加的偏差时会增加。我们最后。我们描述的结果。我们描述的结果。我们描述。我们描述了这个结果。我们最后。我们所呈现的精确性。我们说,我们所呈现的精确性。我们所呈现的精确性的变化。