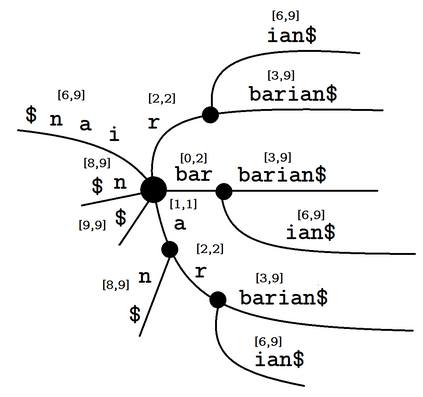
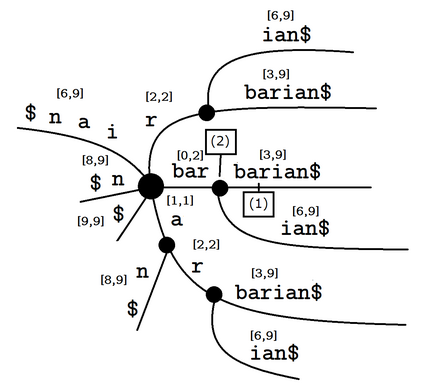
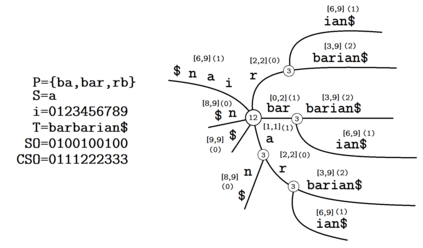
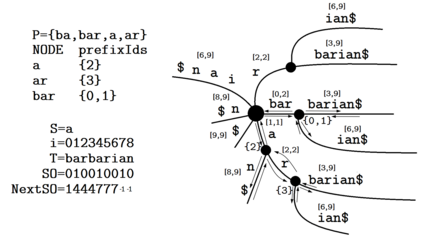
Given two strings $T$ and $S$ and a set of strings $P$, for each string $p \in P$, consider the unique substrings of $T$ that have $p$ as their prefix and $S$ as their suffix. Two problems then come to mind; the first problem being the counting of such substrings, and the second problem being the problem of listing all such substrings. In this paper, we describe linear-time, linear-space suffix tree-based algorithms for both problems. More specifically, we describe an $O(|T| + |P|)$ time algorithm for the counting problem, and an $O(|T| + |P| + \#(ans))$ time algorithm for the listing problem, where $\#(ans)$ refers to the number of strings being listed in total, and $|P|$ refers to the total length of the strings in $P$. We also consider the reversed version of the problems, where one prefix condition string and multiple suffix condition strings are given instead, and similarly describe linear-time, linear-space algorithms to solve them.
翻译:给两个字符串 $T $和 $S $ 和 一 套字符串 $P 美元, 对于每个字符串 $ p $ 美元, 考虑以美元作为前缀和美元作为后缀的独特子字符串 。 然后想到两个问题; 第一个问题是 子字符串的计数, 第二个问题是 列出所有子字符串的问题 。 在本文中, 我们描述两个问题的线性时间、 线性空间后缀树算法 。 更具体地说, 我们描述点数问题的时间算法 $O ( ⁇ T + ⁇ ⁇ + ⁇ P ⁇ ) 美元, 和 美元 + ⁇ P + ⁇ ⁇ + ⁇ ( ans) 美元 。 上市问题的时间算法, 其中 $ ⁇ ( ans) 指的是列出的字符串总数, 和 $ ⁇ P $ $ 美元 的字符串总长度 。 我们还考虑了问题的反向版本, 问题, 其中给出了一个前因质字符串和多个后缀 质字符串 。