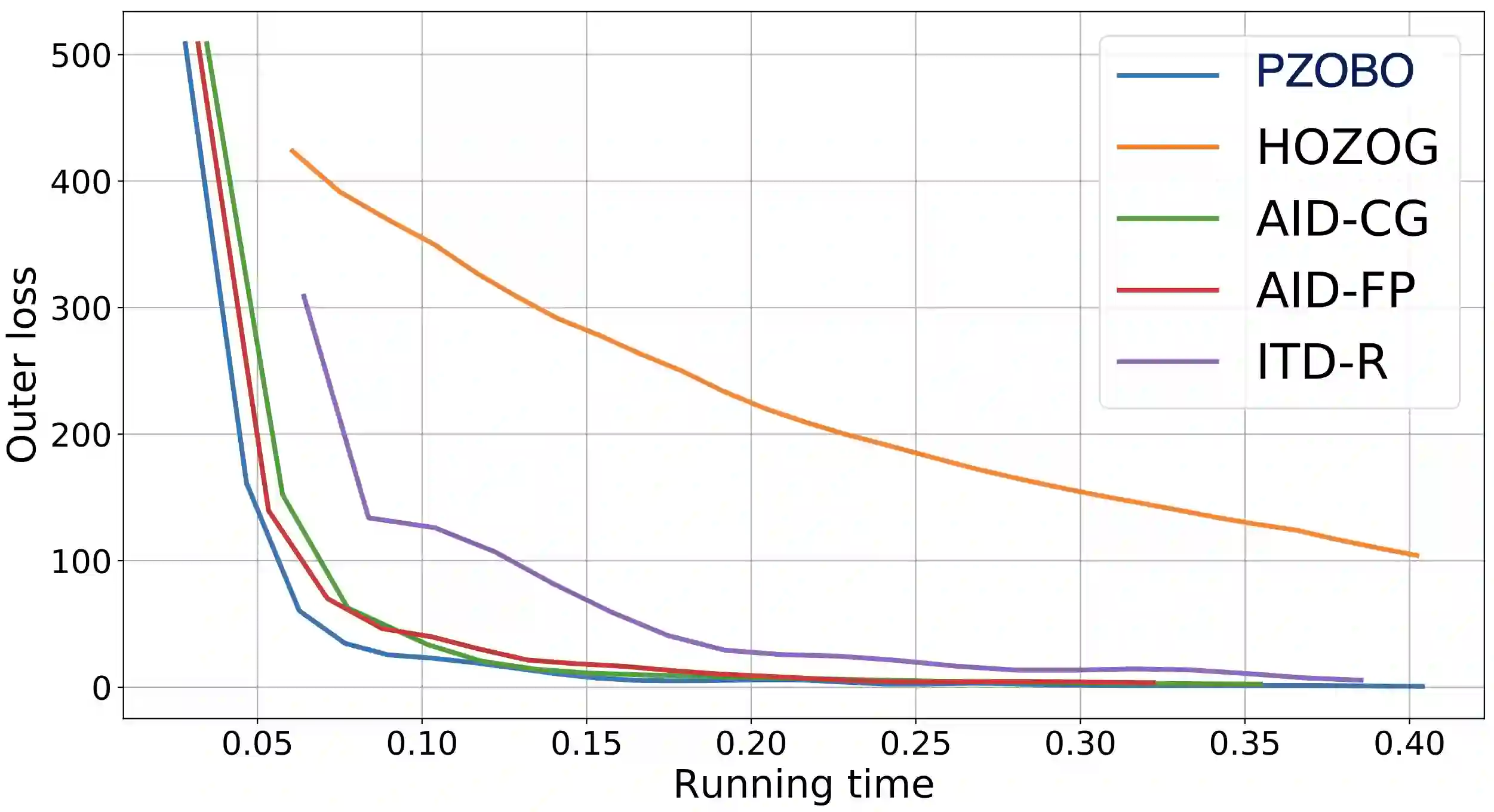
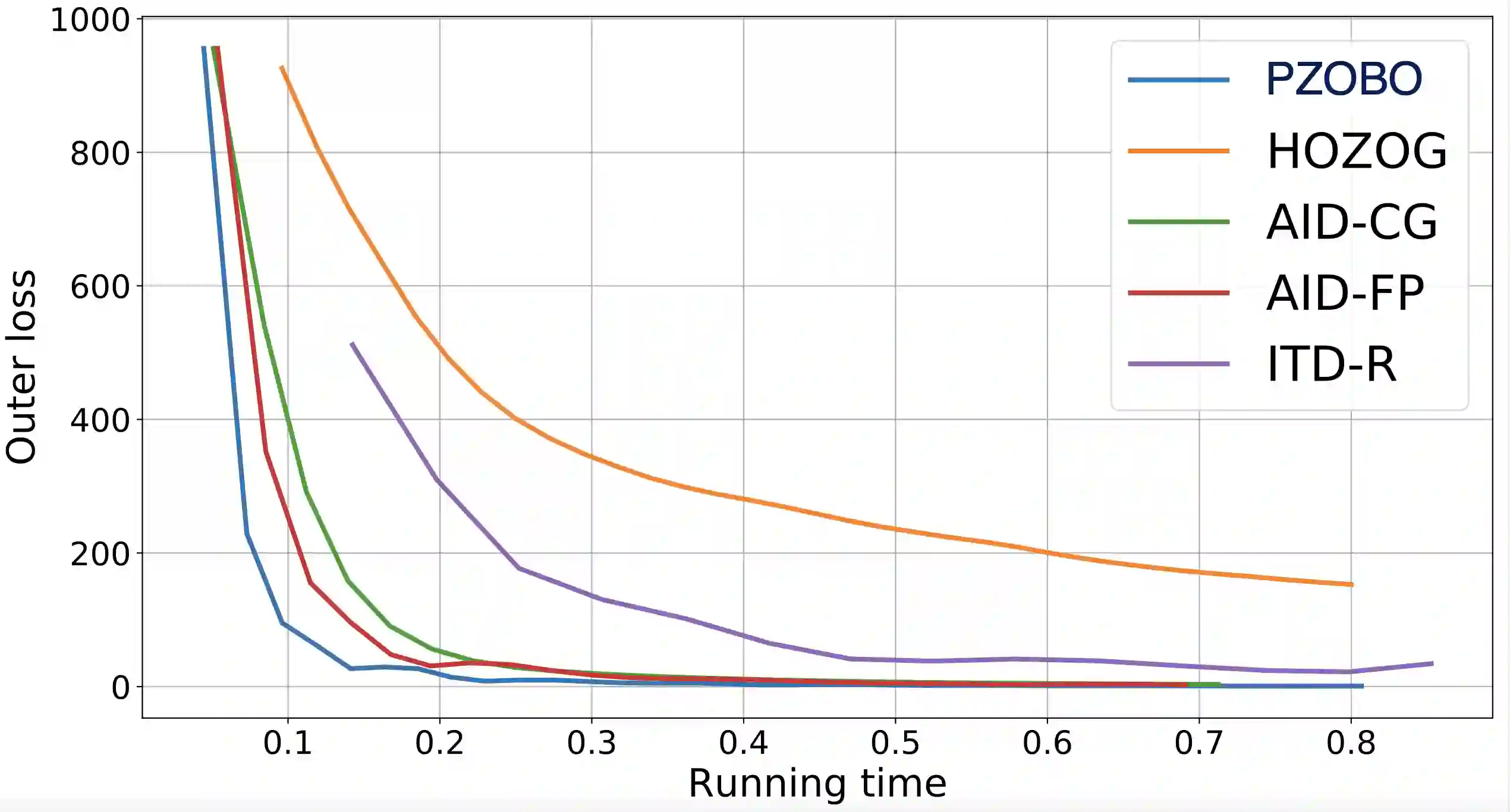
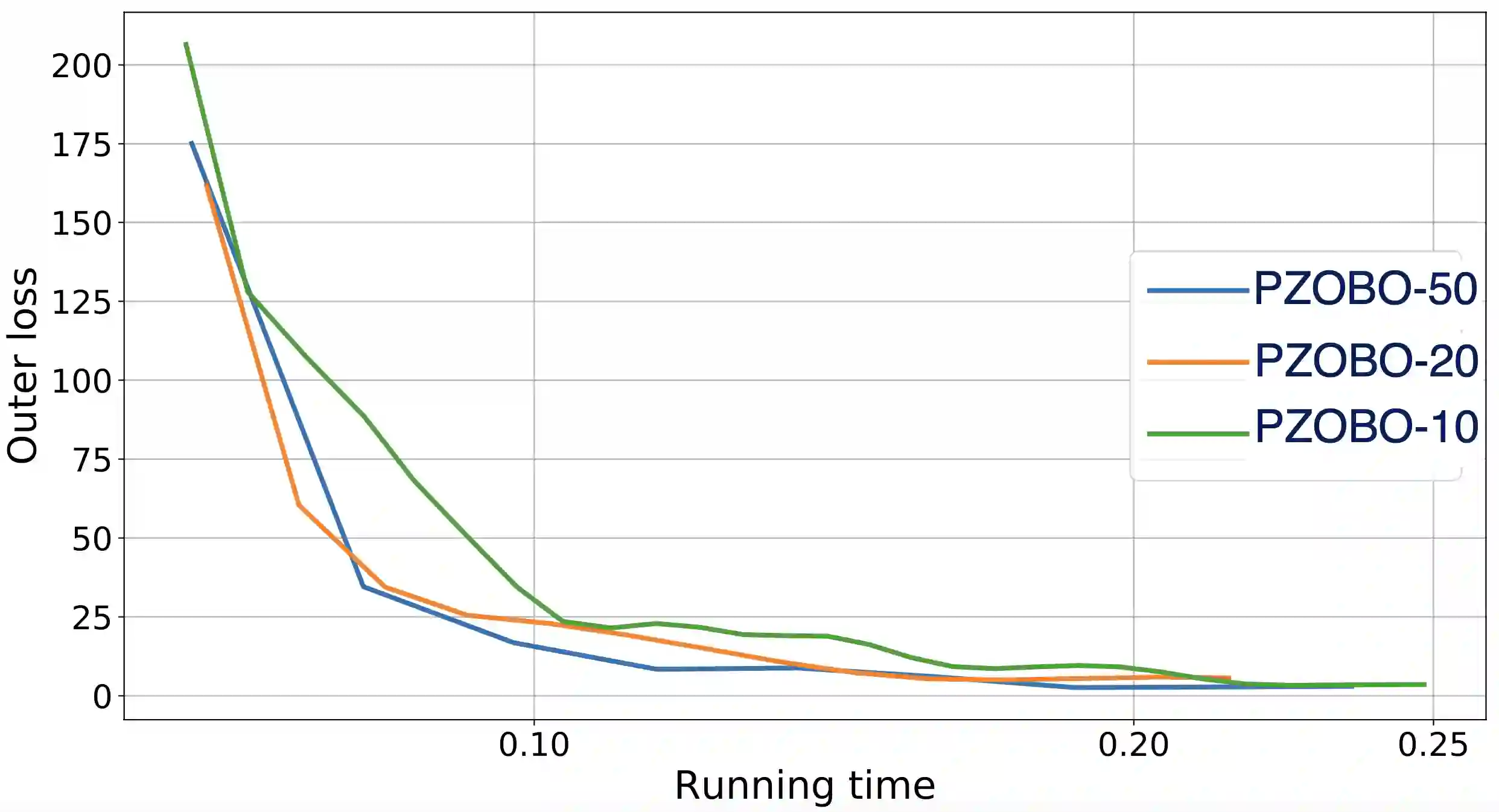
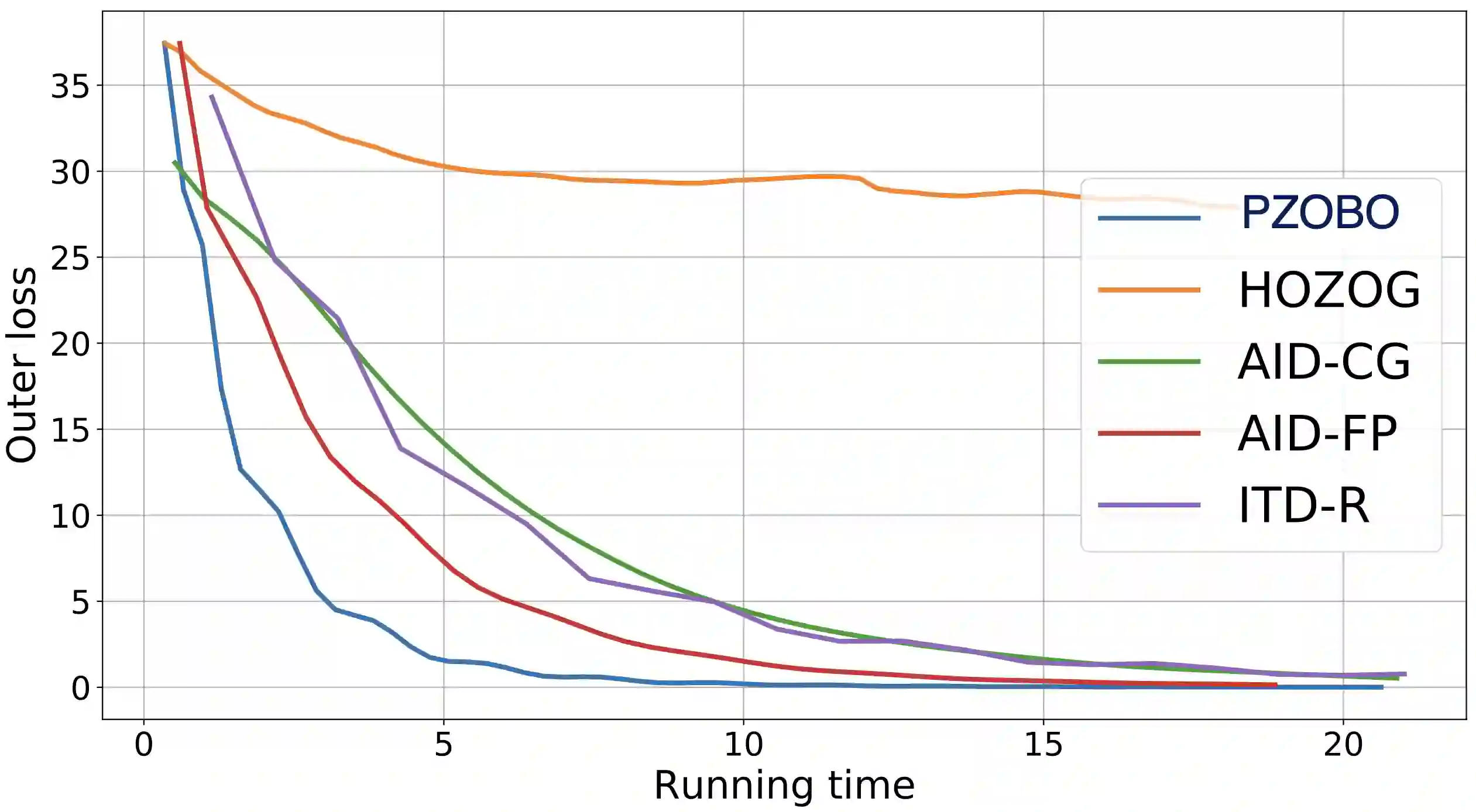
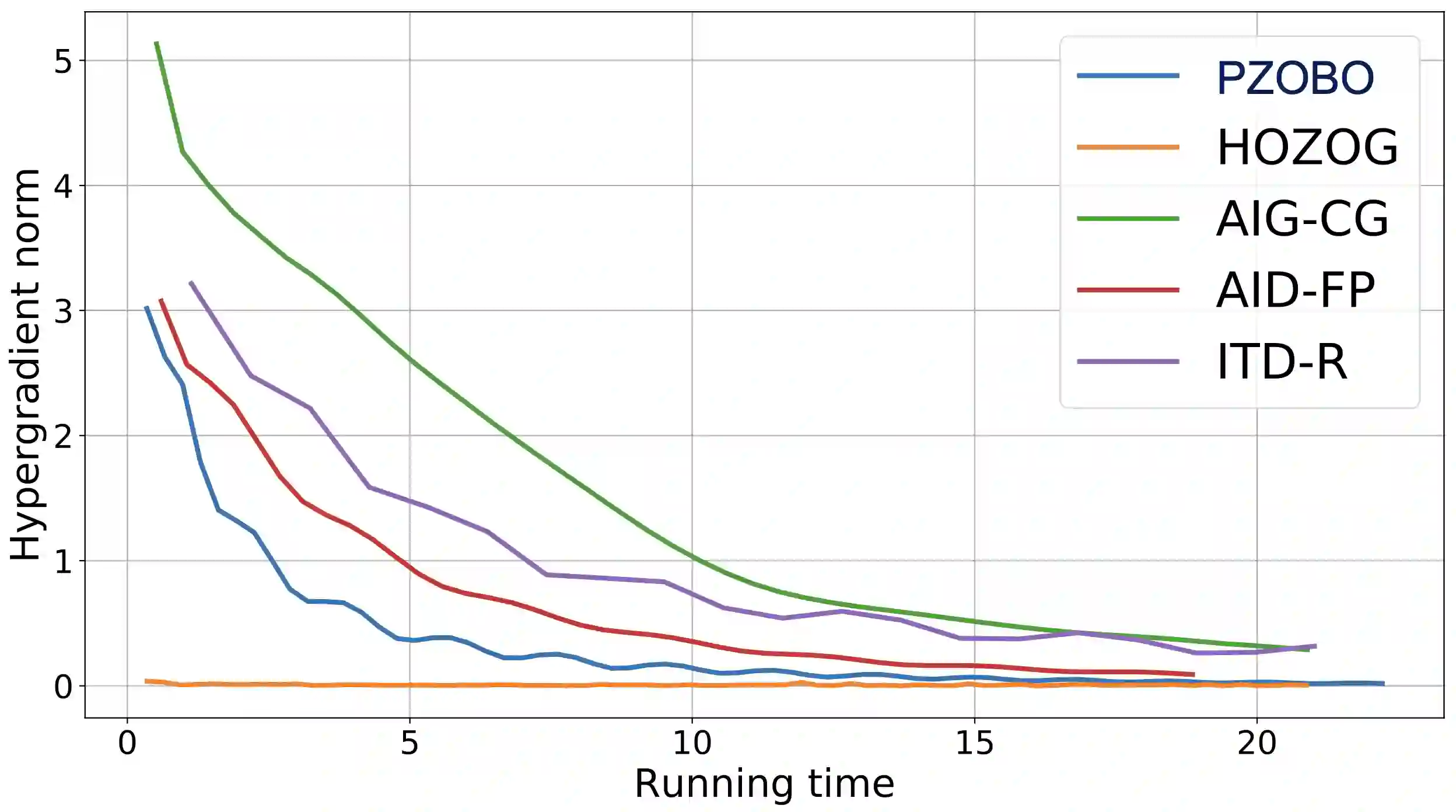
Bilevel optimization has arisen as a powerful tool in modern machine learning. However, due to the nested structure of bilevel optimization, even gradient-based methods require second-order derivative approximations via Jacobian- or/and Hessian-vector computations, which can be costly and unscalable in practice. Recently, Hessian-free bilevel schemes have been proposed to resolve this issue, where the general idea is to use zeroth- or first-order methods to approximate the full hypergradient of the bilevel problem. However, we empirically observe that such approximation can lead to large variance and unstable training, but estimating only the response Jacobian matrix as a partial component of the hypergradient turns out to be extremely effective. To this end, we propose a new Hessian-free method, which adopts the zeroth-order-like method to approximate the response Jacobian matrix via taking difference between two optimization paths. Theoretically, we provide the convergence rate analysis for the proposed algorithms, where our key challenge is to characterize the approximation and smoothness properties of the trajectory-dependent estimator, which can be of independent interest. This is the first known convergence rate result for this type of Hessian-free bilevel algorithms. Experimentally, we demonstrate that the proposed algorithms outperform baseline bilevel optimizers on various bilevel problems. Particularly, in our experiment on few-shot meta-learning with ResNet-12 network over the miniImageNet dataset, we show that our algorithm outperforms baseline meta-learning algorithms, while other baseline bilevel optimizers do not solve such meta-learning problems within a comparable time frame.
翻译:双层优化是现代机器学习的强大工具。 但是,由于双层优化的嵌套结构,甚至基于梯度的方法也需要通过雅各布或赫斯登的计算进行二级衍生衍生物近似,而计算成本可能很高,实际上无法推广。最近,提出了无黑相双层计划来解决这个问题,一般想法是使用零或一阶方法来估计双层问题的全面超升。然而,我们从经验上观察到,这种近似可以导致巨大的差异和不稳定的培训,但只有将雅各克特矩阵作为超升度的一部分来估计反应。为此,我们提出了一个新的无黑相亚方法,采用零阶类方法来通过两种优化路径之间的差异来估计雅各布矩阵的反应。从理论上讲,我们为拟议的双级算法提供了趋同率分析,我们的主要挑战是如何辨别依赖轨迹测基底线框架的近似和顺畅性性质,但只有雅各基矩阵的部分部分的响应才变得非常有效。为此,我们提出了一个新的海相无端方法,即采用零阶平级方法,通过两种优化的双级的亚级模型显示我们所认识的亚级的内测算结果。