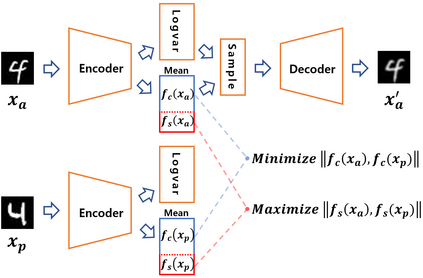
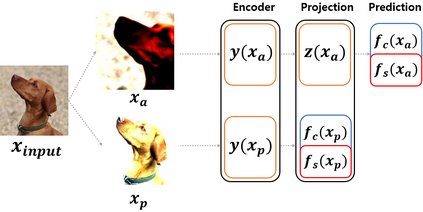
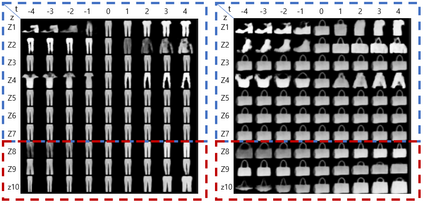
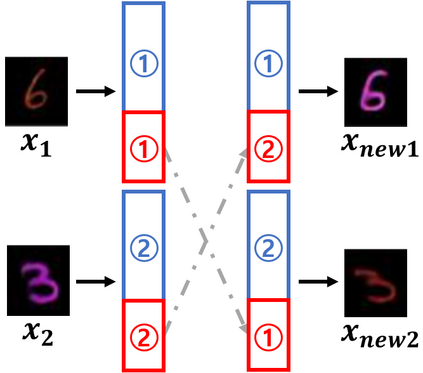
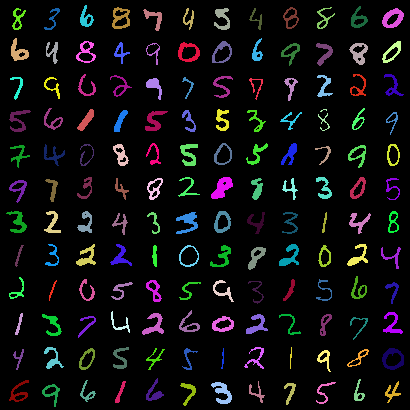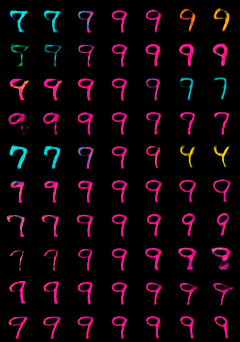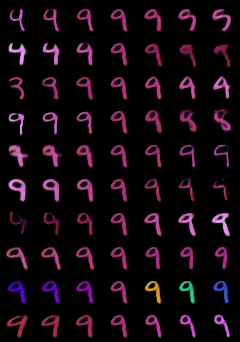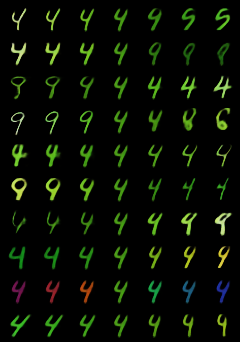In contrastive learning in the image domain, the anchor and positive samples are forced to have as close representations as possible. However, forcing the two samples to have the same representation could be misleading because the data augmentation techniques make the two samples different. In this paper, we introduce a new representation, partitioned representation, which can learn both common and unique features of the anchor and positive samples in contrastive learning. The partitioned representation consists of two parts: the content part and the style part. The content part represents common features of the class, and the style part represents the own features of each sample, which can lead to the representation of the data augmentation method. We can achieve the partitioned representation simply by decomposing a loss function of contrastive learning into two terms on the two separate representations, respectively. To evaluate our representation with two parts, we take two framework models: Variational AutoEncoder (VAE) and BootstrapYour Own Latent(BYOL) to show the separability of content and style, and to confirm the generalization ability in classification, respectively. Based on the experiments, we show that our approach can separate two types of information in the VAE framework and outperforms the conventional BYOL in linear separability and a few-shot learning task as downstream tasks.
翻译:在图像域的对比性学习中,锚和正样样本被迫尽可能有最接近的表达面。然而,迫使两个样本具有相同的表达面可能会造成误导,因为数据增强技术使两个样本不同。在本文中,我们引入了新的表达面,即分隔代表面,通过对比性学习,既可以学习锚和正样的共同和独特特征。分隔代表面由两部分组成:内容部分和风格部分。内容部分代表了该类的共同特征,风格部分代表了每个样本的特征,这可能导致数据增强方法的表述。我们可以通过将对比性学习的损失功能分解为两个术语,分别在两个不同的表述上。为了用两个部分来评估我们的代表面,我们采用了两个框架模型:动态自动电解码(VAE)和布茨带(Boutsstraptractour Own Lent)(BYOL),以显示内容和风格的分离性,并证实分类中的概括性能力,这可以导致数据增强方法的体现。根据实验,我们的方法可以在两个单独的表达式学习功能中将两种类型在常规任务A级框架和低层学习中,即常规任务。