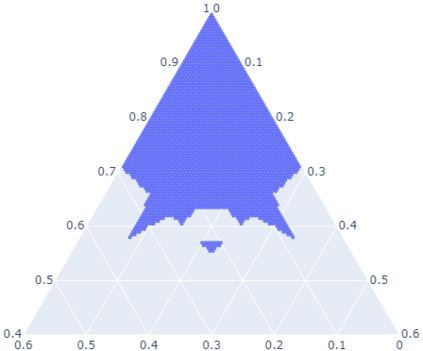
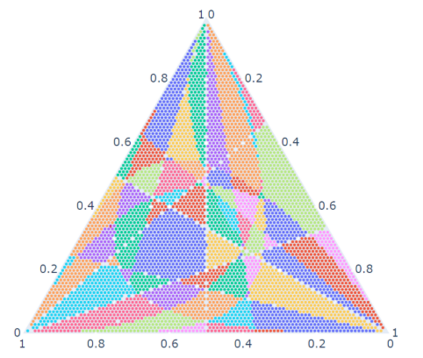
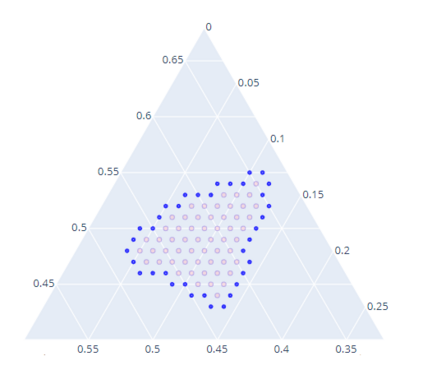
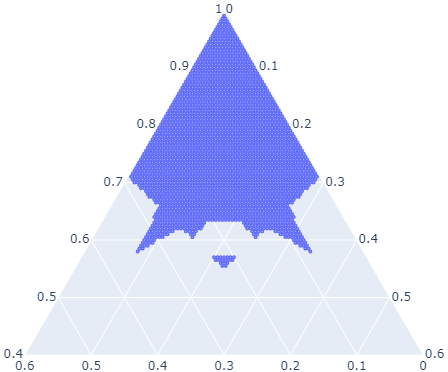
Computation of confidence sets is central to data science and machine learning, serving as the workhorse of A/B testing and underpinning the operation and analysis of reinforcement learning algorithms. This paper studies the geometry of the minimum-volume confidence sets for the multinomial parameter. When used in place of more standard confidence sets and intervals based on bounds and asymptotic approximation, learning algorithms can exhibit improved sample complexity. Prior work showed the minimum-volume confidence sets are the level-sets of a discontinuous function defined by an exact p-value. While the confidence sets are optimal in that they have minimum average volume, computation of membership of a single point in the set is challenging for problems of modest size. Since the confidence sets are level-sets of discontinuous functions, little is apparent about their geometry. This paper studies the geometry of the minimum volume confidence sets by enumerating and covering the continuous regions of the exact p-value function. This addresses a fundamental question in A/B testing: given two multinomial outcomes, how can one determine if their corresponding minimum volume confidence sets are disjoint? We answer this question in a restricted setting.
翻译:信任度的计算是数据科学和机器学习的核心,是A/B测试的工作马,是强化学习算法的运作和分析的基础。本文研究多数值参数最小容量信任度组的几何学分。当使用信任度组取代基于界限和无线近似的更标准的信任度组和间隔时,学习算法可以显示出更高的样本复杂性。先前的工作显示最低容量信任度组是由精确的 p值定义的不连续功能的层次组。信任度组在它们拥有最小平均体积方面是最佳的,但计算一组中单一点的会籍对规模小的问题具有挑战性。由于信任度组是不连续功能的等级组,因此其几何形状不明显。本文通过计算和覆盖精确的p价值函数的连续区域来研究最低数量信任度组的几何分法。这涉及到A/B测试中的一个基本问题:鉴于两个多数值结果,如何确定它们相应的最小数量信任度组是否不连贯?我们在一个限制性的设置中回答这个问题。