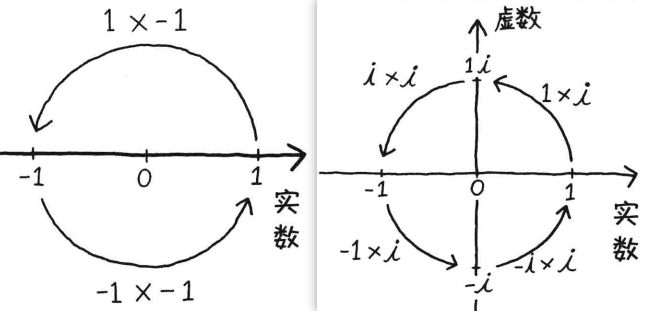
三角学中，这么一堆公式其实就说了2个事而已

[遇见数学创作小组] 作者: 心如止水

心如止水，Java程序员。善于把复杂的数学知识，简洁易懂地表达出来

★提示: 如果文中数字/公式显示较大, 请点击右上角中"刷新"即可恢复正常. 加入 [创作小组] 请点击这里. 

在学三角这部分的时候，有些书习惯列出诱导公式(induction formula)，都列出来的话可以写小半张纸。

➣ 那什么是“诱导公式”呢？

“诱导公式”应该是一个老的翻译，“诱导”也就是我们今天所说的“推导”，除了公理之外，那有什么公式不是推导出来的呢？所以说起这种名字就意味着根本就没有名字，因为实在太显而易见了，所以没有人好意思大叫“尤里卡”，没有人好意思冠名。

但是没有名字，交流起来又不方便，所以就干脆这么叫了，这种叫法类似于“孩他娘”。

➣ “显而易见”在哪里？

一堆式子本质上只说了两件事情：

① 乘上 -1 的几何意义是转 ，乘上 i 就是旋转 。

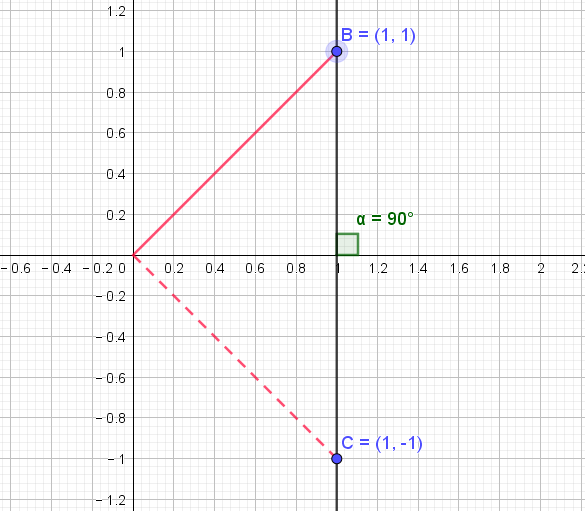
②  的几何意义是  轴对称。

上面是两个老调重弹，然后，再结合两个显而易见的已知事实：

③   的几何意义是不变。

④ co 的含义是余角。

这就是所有的“诱导公式”。

你可以看出，这说的都是些最基础的东西，角函数就是这样的地位：它是二维在一维的投影；旋转和平移的桥梁；可以看做比值，它却有简洁的几何定义。

➣ 如此简单的事实是怎么变成那么多公式的？

首先，诱导公式并不是用几何形式写的，而用函数语言写的，所以你需要换一种表示方法，或者说换一种观察角度。而我们对这种角度是陌生的，所以就容易产生混乱的感觉，只要习惯了是一样的。

其次，之所以诱导公式能写很长一串，就是因为把 tan/sec/cot/csc 都印上去了，其实这些都可以通过 sin/cos 的变化一眼就看出来，印上去是为了实际的查阅方便，不是为了记忆。不解释一下会“吓人一跳”，懂了之后就很简单，看似很多，其实就那么回事。

➣怎么样从几何视角转换为函数视角呢？

①  和 

①  和 

其实就是复数的乘法

②  和 

 可以看作投影，“平面上关于  轴 对称的点”，在  轴 的投影自然是一致的， 轴的投影刚好符号相反。

③ 和 

任何角转一圈，从静止的角度来看都是不变的。

④  和 

cos 的 意思是余角的正弦 ，余角的余角还是原来的角，所以 -α 就是在原来角和余角之间切换。

➣ 实际该怎么使用呢？

之所以罗列出诱导公式，最重要的目的就是忘记的时候，对照查阅的，如果你手边没有对照表，其实只要动动脑筋就可以想明白：

● 这些变化都是以  为单位的，所以说只要看到  的倍数，就知道可以应用诱导公式。

● 如果是  奇数倍就是在原来角和余角之间切换，如果是  奇数倍就是  ；如果是  的奇数倍，就是 ×-1 ；如果发现是上述情况，但是符号不对，那就通过取对称变换符号。

真正重要的公式是“积化和差”，从名字就会看出这个东西有降次作用，在对数表发明之前，天学家们就已经用这个公式来简化计算了，纳皮尔发明对数表，也可能受到了它的启发。

参考资料

• https://zh.wikipedia.org/wiki/诱导公式