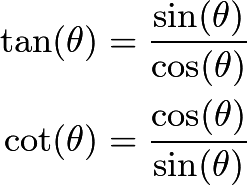单位圆与三角函数

小贴士

如文中公式显示较大, 请点击右上角中"刷新"即可恢复正常. 小编正在整理本文可操纵版的PPT文档, 明日票圈发布下载地址, 敬请关注微信. 

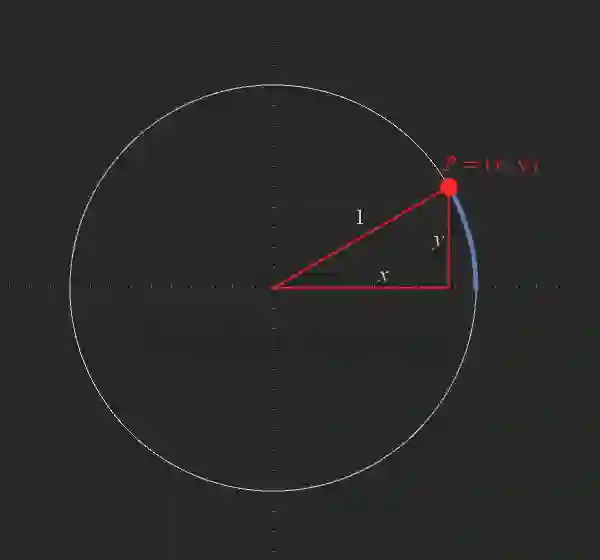
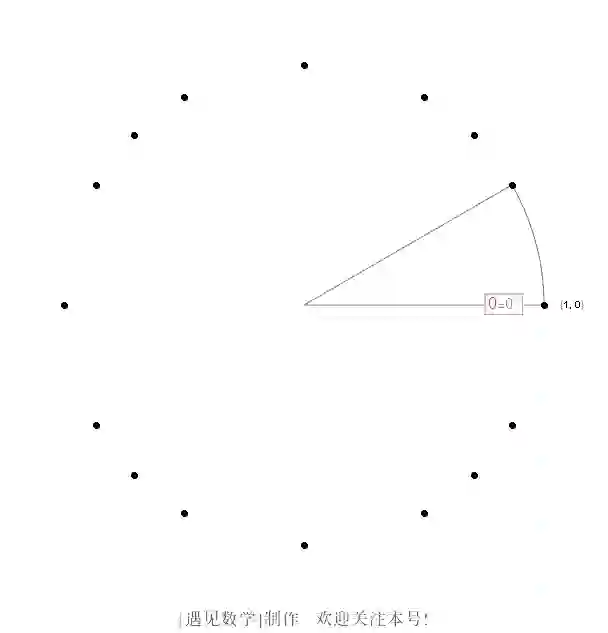
单位圆(Unit circle)是指坐标为原点, 半径为长度为 1 的圆. 单位圆对于三角函数和复数的坐标化表示有着重要意义. 如果给定一个角度  则为逆时针转动, 比如转到单位圆上的点 .

▌角度与弧度
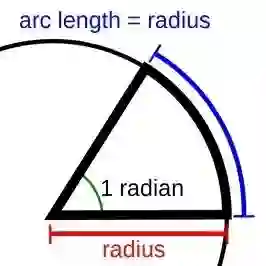
在三角学中, 角度除了可以用度(°)来表示, 为了方便起见, 常使以弧度(Radian)为单位, 通常不写出弧度单位, 或就简写为 rad. 单位弧度定义为圆弧长度等于半径时的圆心角. (下图自维基)

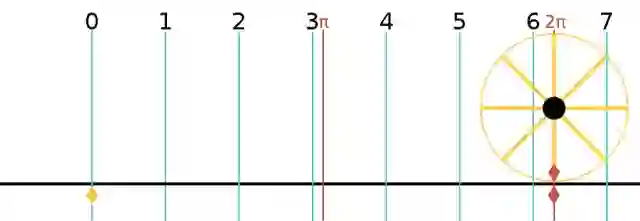
一个完整的圆的弧度是2π. 下面是单位圆圆周滚动一周  的动画(下图自维基):

弧度和度数之间的转换有下面等式:

也请观察下面动画:

下面图中是在度和弧度之间转换的动画, 注意  角均用弧度制和角度制表示.  角所对应的单位圆上的点的坐标为 .

在微积分和大多数数学科目中, 角度通常用弧度来衡量. 因为弧度单位会带来很多计算上的简便, 以及可以推导出很多漂亮的等式. (推荐阅读《角的疑惑——为什么使用弧度？》).

▌拥有不同长度的单位圆

数学家也用其他距离测量来定义更一般化的"单位圆", 关于这个有趣的话题请观看 [遇见数学] 翻译小组的这个视频《当 π 不等于 3.14》.

▌单位圆与三角函数
三角函数可以由单位圆来定义. 如果点  位于单位圆上, 那么斜边的长度即为单位圆半径 1. 根据勾股定理, 和  满足等式:

又因为 , , 得到下面恒等式:

单位圆上一点到  轴的距离是这个角的正弦  , 到  轴的距离则是这个角的余弦 cosine(  ). 观察下图很好地解释了正弦和余弦是怎么回事.

不仅是正弦与余弦, 其余四个标准三角函数: 正切(), 余切(), 正割(), 余割() 都可以在单位圆表示出来.
一个角的正切 tangent() 是  除以  , 余切 cotangent ( )则是  除以 sin.

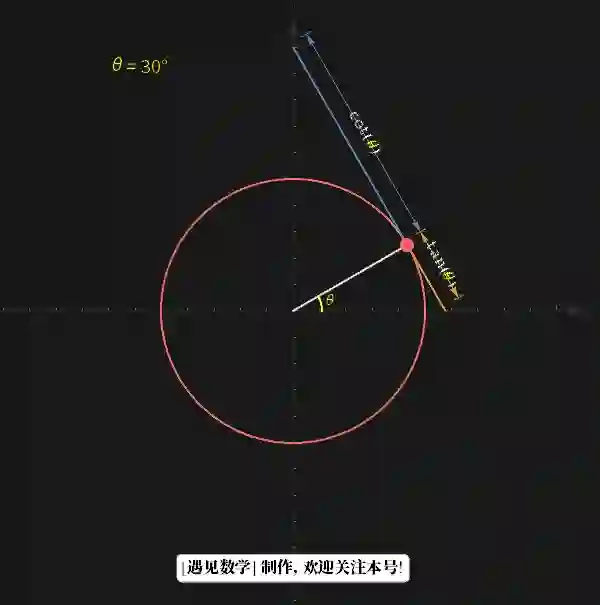
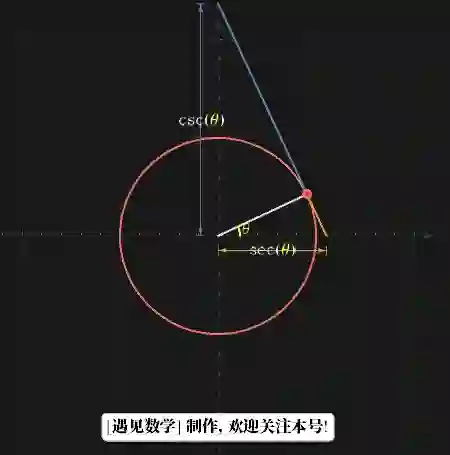
而对  和  在单位圆上有一种漂亮的几何解释, 如果过  角单位圆上的点, 画出圆的切线, 那么切线和  轴交点之间的距离, 就是这个角度的  , 这个点与切线和  轴的交点的距离, 就是这个角度的 . 这种解释能让人直观感受这两个值的意义. 观察下面动图, 看看余切何时变小, 正切何时变大.

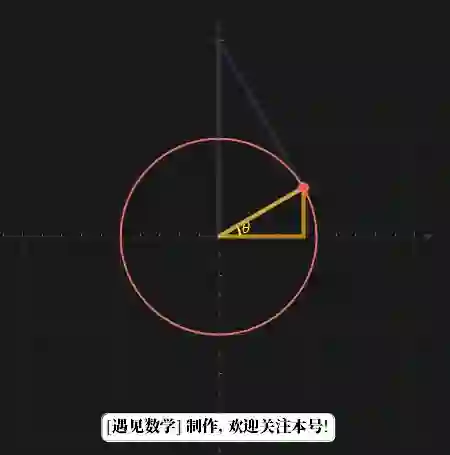
类似地, 正割 secant() 的定义是 , 而余割 cosecant ()的定义是 , . 在可以根据下图所示的两个相似三角形来证明(感兴趣的可以动手做下).

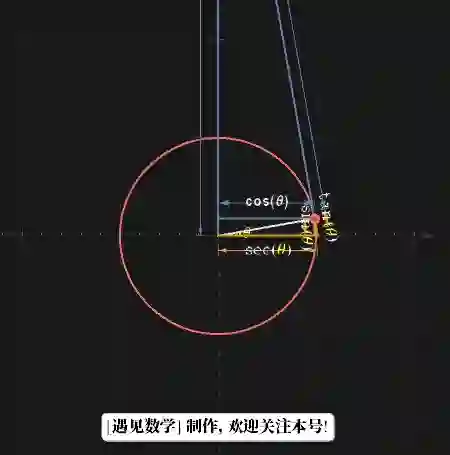
并且  和  也有类似的几何解释, 当切线与  轴的交点到原点的距离就是这个角度的  , 而切线与  轴的交点到原点的距离则是这个角度的 .

还有一点值得注意的地方, ,  和  对应线段的长度都与  轴有关系.

而 ,  和  对应的线段长度都与  轴有关系, 这里不再重复绘制. 我们只将这  个三角函数它们一并绘制出来.

▌复平面上的单位圆
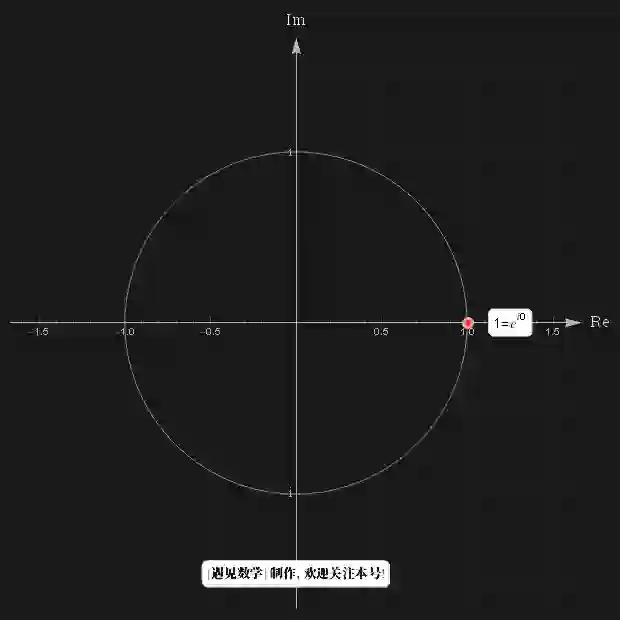
复平面上的单位圆, 也就是复数  的形式:

 函数又称纯虚数指数函数, 是复变函数的一种, 和三角函数类似，其可以使用正弦、余弦函数来定义.
观察下图不同的  值对应的 , 请留意动画停顿之处(特别是在复平面中等于  的地方).

对于不在单位圆上的点, 你只需乘以  , 也就是如果  和  为相同的点, 则 
从上图中可以得知  关于  是周期的, 且周期为  . 这意味着  (完)