贝叶斯网络入门

论智

作者 | weakish

来源 | 论智

我们昨天介绍了朴素贝叶斯分类器，通过假设每一个特征的出现都是独立事件，简化了计算复杂度，也避免了样本稀疏的问题。虽然这一假设常常是不准确的，但朴素贝叶斯在实际工程中出乎意料地好用。因为很多应用并不在乎精确的类概率，只关心最后的分类结果。

然而，当特征之间相关性比较强，而我们又要求比较精确的类概率的时候，朴素贝叶斯就不够用了。

也就是说，下面的式子里p [f1, f2 .. fn]不好算了。

pSucc [f1, f2 .. fn] S =
    (p S) * (pSucc S [f1, f2 .. fn]) / (p [f1, f2 .. fn])

回顾一下，如果[f1, f2 .. fn]是独立事件，那我们有：

p [f1, f2 .. fn] =
    (p f1) * (p f2) * .. * (p fn)

现在每一项特征的概率可能受其他特征的影响。假设有一个函数pp可以表达这些影响：

p [f1, f2 .. fn] =
    (pp f1) * (pp f2) * .. * (pp fn)

那么问题就在于pp是如何定义的？

既然pp表达的是某一事件受其他事件的影响，那pp就可以用条件概率来定义：

pp f = pSucc (influenced f) f

对于给定的特征f，我们找出所有影响它的特征[inf1, inf2 .. infn]：

influenced f =
    pSucc [inf1, inf2 .. infn] f

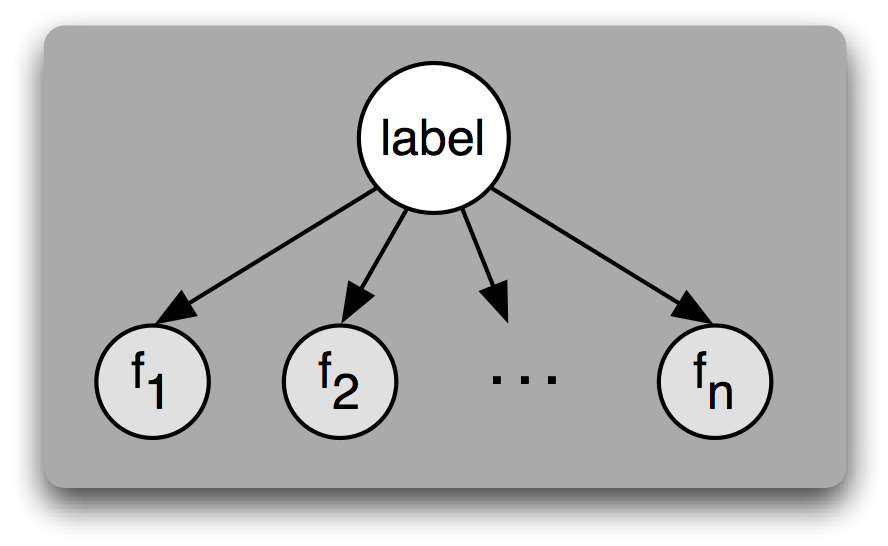
pSucc [inf1, inf2 .. infn] f这看起来是不是很熟悉？我们讨论幼稚贝叶斯的时候提到的是pSucc [f1, f2 .. fn] S。这两者的结构是一样的。

因此，这其实是一个递归调用幼稚贝叶斯分类器的问题。

基于同样的思路，我们可以处理(pSucc S [f1, f2 .. fn]).

不过实际工程中，因为数据量很大，递归调用贝叶斯分类器是吃不消的。所以为了降低计算复杂度，我们需要进行一些简化：

1. 当影响程度很低时，我们直接忽略，视为独立事件。

2. 我们只考虑直接影响给定特征f的特征，不考虑间接影响。例如，pinf1可能通过影响inf1来间接影响f，这种情况不考虑。

3. 当我们考虑影响给定特征f的特征时，假定这些影响f的特征是相互独立事件。

当然，如果有必要，上面的简化也可以放宽，以提高计算复杂度为代价，获得更准确的估计。

进行上述简化后，我们得到了贝叶斯网络(Bayesian network)。

一个简单的贝叶斯网络

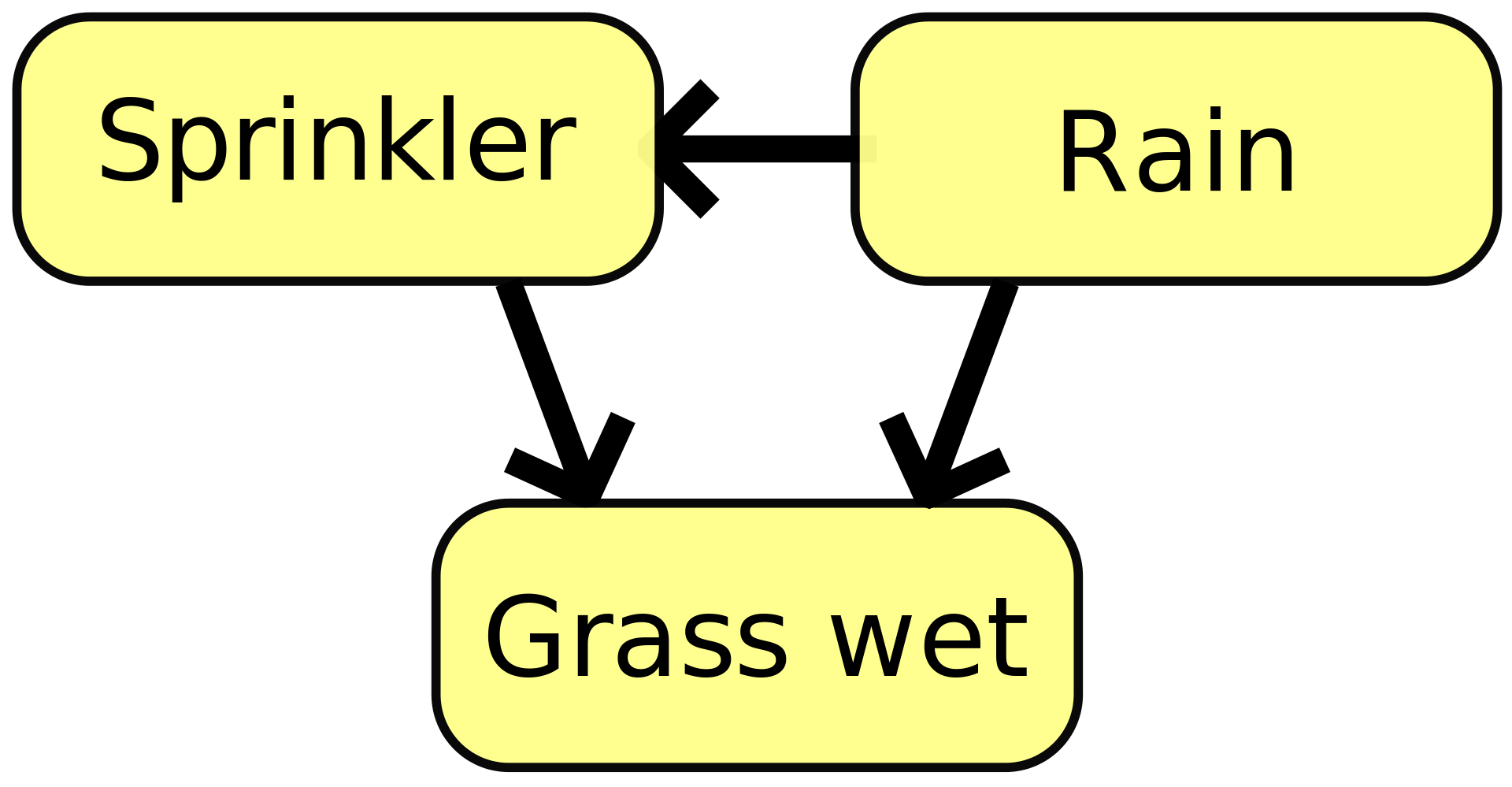
贝叶斯网络中，特征间的相互影响关系，我们用有向无环图（DAG）来表示。在数学上，我们用图（Graph）来表示对象间的相互关系。图由结点（代表对象）和边（代表关系）组成。如果边具有方向，那么得到的图就称为有向图。对于一个有向图而言，如果从任一节点出发，都无法经过若干条边回到该节点，那么这个有向图就称为有向无环图。在贝叶斯网络中，我们用有向无环图的边的方向，表示某个特征对另一个特征的影响。无环则保证特征间的相互影响关系不会陷入无穷无尽的循环。

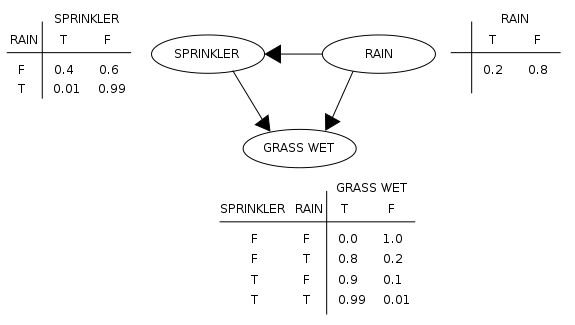
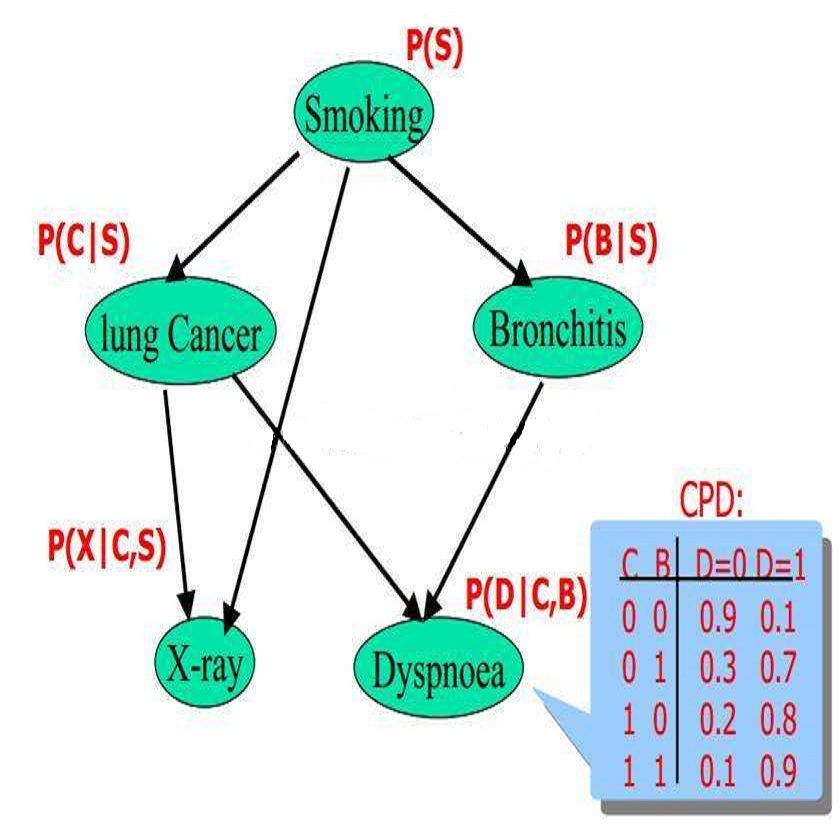
特征对给定特征的具体影响程度，我们用条件概率表(CPT)来表示。条件概率表这个概念很容易理解。下图就展示了一个简单的贝叶斯网络中各特征的条件概率表。

最后，特征间的相互影响关系，也就是DAG的构建，依赖于经验或领域知识。条件概率表，则可以用朴素贝叶斯来改进。

本文系论智编译，转载请联系本公众号获得授权。