人工神经网络之正反向传播

引言

考你一道非常简单的题，给定表达式 

    e = (a+b) × (b+1)

并给定一组 a 和 b 值，比如 a = 2, b = 1，计算

1. e 的值

2. e 对 a, b 的变化率 (也就是 a, b 变化 1 个单位，求出 e 变化多少个单位)

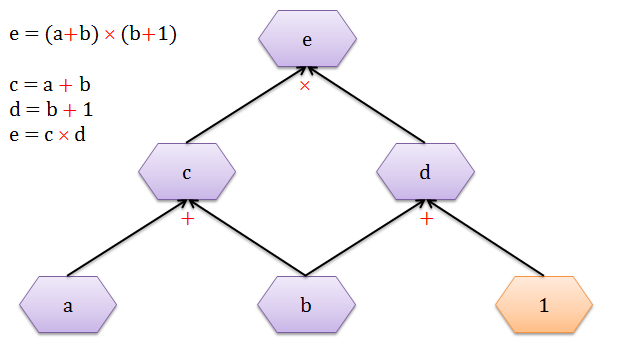
用 c = a + b，d = b + 1 的代换，画出下面的计算图 (computational graph)。图中有三个运算符：2 个加法 (+) 和 1 个乘法 (×)。紫色六边形里面的是变量，橙色六边形里面是常数。

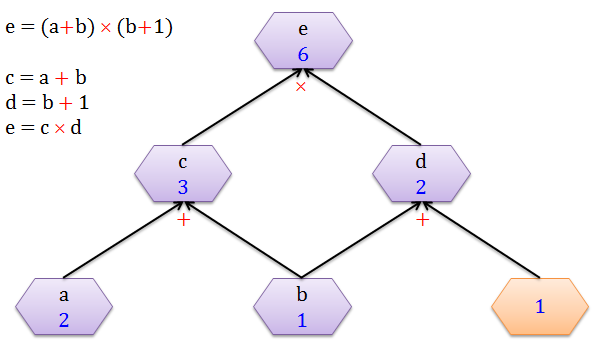
当 a = 2, b = 1 时，从下往上 (黑色箭头) 的计算出 c = 3, d = 2 以及 e = 6。整个过程就是正向传播 (forward propagation)，顾名思义就是沿着正方向做一些计算。

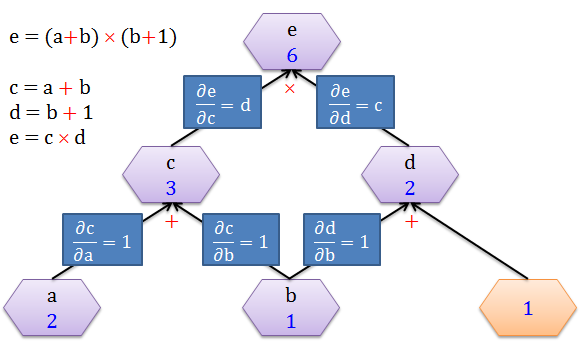
接下来要计算 e 对 a, b, c, d 的变化率，首先来看看在每条边 (edge) 的导数 (derivative)，如下图：

因为 c = a + b

 

• 当 a 变化 1 个单位，c 变化 1 个单位，∂c/∂a = 1/1 = 1

• 当 b 变化 1 个单位，c 变化 1 个单位，∂c/∂b = 1/1 = 1

因为 d = b + 1

• 当 b 变化 1 个单位，d 变化 1 个单位，∂d/∂b = 1/1 = 1
  

因为 e = c × d

• 当 c 变化 1 个单位，e 变化 d 个单位，∂e/∂c = d/1 = d

• 当 d 变化 1 个单位，e 变化 c 个单位，∂e/∂d = c/1 = c

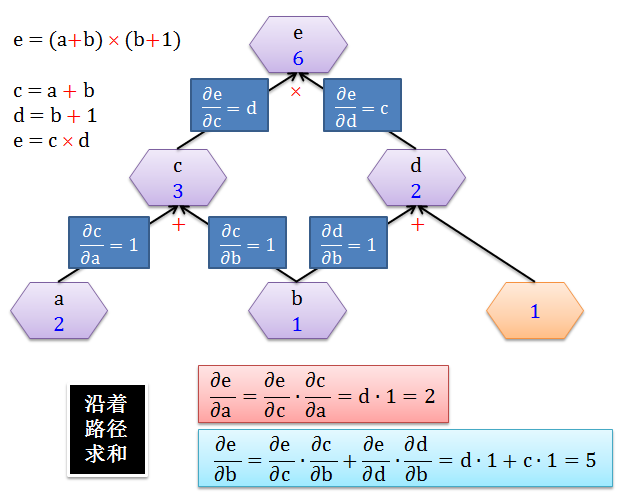
有了每条边上的导数，计算 e 对于 a 或 b 的变化率就是加总所有经过 a 或 b 的路径 (sum over path)，如下图所示：

很显然

• ∂e/∂a 只有一条路径，可以理解当 a 变化 1 个单位，则 c 变化 1 个单位，则 e 变化 2 个单位，因此 ∂e/∂a = ∂e/∂c × ∂c/∂a = 2

  
  

• ∂e/∂b 只有两条路径，可以理解当 b 变化 1 个单位
  

  
  

• c 变化 1 个单位，则 e 变化 2 个单位

• d 变化 1 个单位，则 e 变化 3 个单位

  
  

因此 ∂e/∂b = ∂e/∂c × ∂c/∂b + ∂e/∂d × ∂d/∂b = 2 + 3 = 5

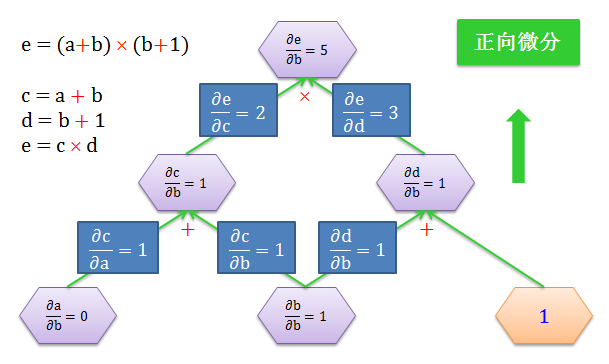
在计算变化率问题上，有两种类型：

1. 从 b 开始正向往上计算所有节点上的变量对 b 的导数，该操作叫做正向微分 (forward-mode differentiation)

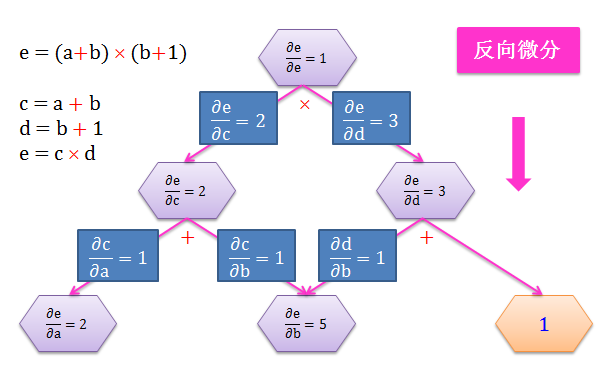
2. 从 e 开始反向往下计算 e 对所有节点上的变量的导数，该操作叫做反向微分 (backward-mode differentiation)

如下面两图所示：

在该问题中，e 是输出：

• 做一次正向微分只能得到 e 对一个输入 (比如 b) 的变化率

• 做一次反向微分却能得到 e 对所有输入 (a, b, c, d) 的变化率

在神经网络 (artificial neural network, ANN) 里面，把 e 当成代价函数，a, b, c, d 当成权重，在梯度下降求权重最优解时就需要代价函数对所有权重的偏导数 (变化率的极限说法)。那么明显反向微分是我们需要计算偏导数的方式。而反向微分这个过程在 ANN 里面的术语称为反向传播 (backward propagation, backprogapation)，顾名思义就是沿着反方向做一些计算。

第一章以极度细微的方式介绍构成 ANN 的基本元素，比如层、节点、箭头、转换函数、权重和分数，并写出 ANN 漂亮的代数和矩阵表达形式；第二章主讲正向传播和反向传播，数学符号非常繁重，但是每小节都有一个简单例子入手帮助理解后面严谨的数学推导；第三章用 Matlab 代码实现一个简单的识别手写数字的 ANN。

目录

第一章 - 前戏王

    1.1 层

    1.2 节点

    1.3 箭头

    1.4 转换函数

    1.5 权重和分数

    1.6 数学表达形式

    1.7 矩阵表达形式

    1.8 链式法则

第二章 - 理论皇

    2.1 正向传播

    2.2 梯度下降

    2.3 反向传播

第三章 - 实践狼

    3.1 问题描述

    3.2 数据解析

    3.3 正向传播

    3.4 反向传播

    3.5 梯度检验

    3.6 其他技巧

总结

第一章 - 前戏王

本节目的是弄清神经网络的里面每个概念和了解其运作，为了达到此目的，我们必须介绍一套系统的数学符号。咋一看可能会头晕目眩，但是相信我一定能给你讲明白，花点时间捋清它们是绝对值得的。

首先以极简的方式来概括神经网络，

• 神经网络是分层 (layer) 的

• 每层上是有节点 (node) 的

• 节点和节点之间是由箭头 (arrow) 连接的

• 节点上有转换函数 (transfer function) 的

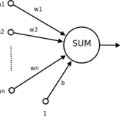
• 箭头是承载着权重 (weight) 的

之后从最初输出开始，权重乘以输出加工成分数，分数通过转换函数生成输出，一层一层，生生不息，直到最后。。。

1.1

层

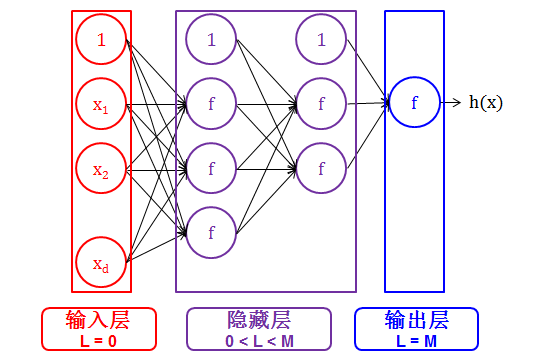
神经网络是分层 (layer) 的。

神经网络的每层用 L 表示，其中 L = 0, 1, 2, …, M.

 

• 输入层 (input layer) 严格来说不被认为是层，因此用 0 层表示

• 输出层 (output layer) 决定神经网络的最终输出

• 隐藏层 (hidden layer) 夹在输入层和输出层的中间

转自：王的机器

完整内容请点击“阅读原文”