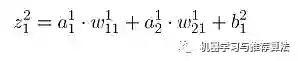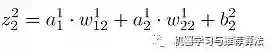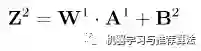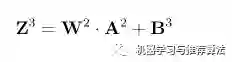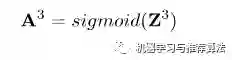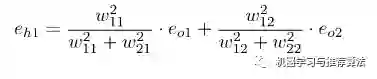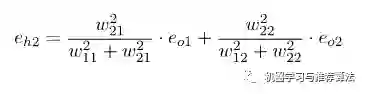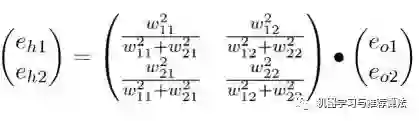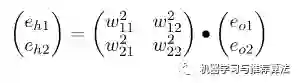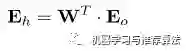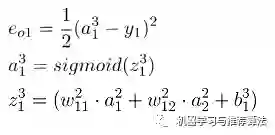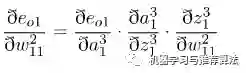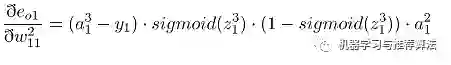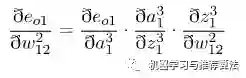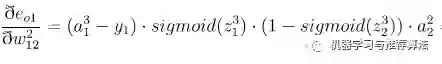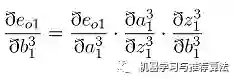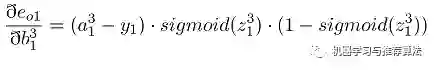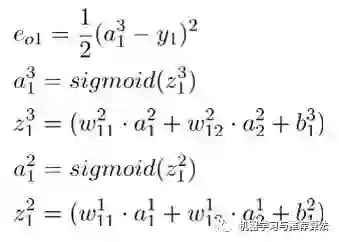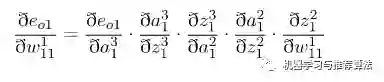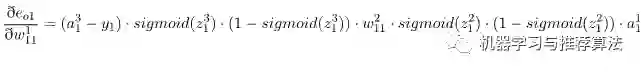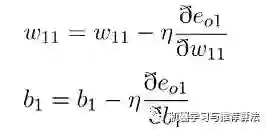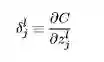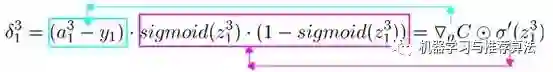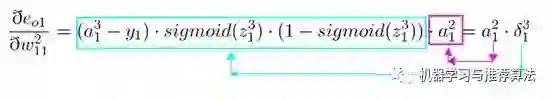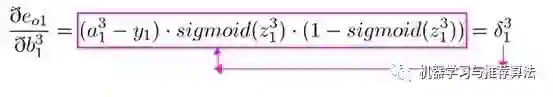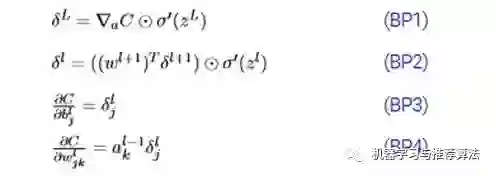一文搞懂反向传播

懒人目录

一、前言

二、举个栗子

三、完整流程

四、链式求导

五、引入delta

一、前言

这是一场以误差（Error）为主导的反向传播（Back Propagation）运动，旨在得到最优的全局参数矩阵，进而将多层神经网络应用到分类或者回归任务中去。

前向传递输入信号直至输出产生误差，反向传播误差信息更新权重矩阵。 这两句话很好的形容了信息的流动方向，权重得以在信息双向流动中得到优化，这让我想到了北京城的夜景，车辆川流不息，车水马龙，你来我往(* ॑꒳ ॑* )⋆*。

至于为什么会提出反向传播算法，我直接应用梯度下降（Gradient Descent）不行吗？想必大家肯定有过这样的疑问。答案肯定是不行的，纵然梯度下降神通广大，但却不是万能的。梯度下降可以应对带有明确求导函数的情况，或者说可以应对那些可以求出误差的情况，比如逻辑回归（Logistic Regression），我们可以把它看做没有隐层的网络；但对于多隐层的神经网络，输出层可以直接求出误差来更新参数，但其中隐层的误差是不存在的，因此不能对它直接应用梯度下降，而是先将误差反向传播至隐层，然后再应用梯度下降，其中将误差从末层往前传递的过程需要链式法则（Chain Rule）的帮助，因此 反向传播算法可以说是梯度下降在链式法则中的应用。

二、举个栗子

为了帮助较好的理解反向传播概念，对它有一个直观的理解，接下来就拿猜数字游戏举个栗子。

2.1 两人猜数字

这一过程类比没有隐层的神经网络，比如逻辑回归，其中小黄帽代表输出层节点，左侧接受输入信号，右侧产生输出结果，小蓝猫则代表了误差，指导参数往更优的方向调整。由于小蓝猫可以直接将误差反馈给小黄帽，同时只有一个参数矩阵和小黄帽直接相连，所以可以直接通过误差进行参数优化（ 实棕线 ），迭代几轮，误差会降低到最小。

2.2 三人猜数字

这一过程类比带有一个隐层的三层神经网络，其中小女孩代表隐藏层节点，小黄帽依然代表输出层节点，小女孩左侧接受输入信号，经过隐层节点产生输出结果，小蓝猫代表了误差，指导参数往更优的方向调整。由于小蓝猫可以直接将误差反馈给小黄帽，所以与小黄帽直接相连的左侧参数矩阵可以直接通过误差进行参数优化（ 实棕线 ）；而与小女孩直接相连的左侧参数矩阵由于不能得到小蓝猫的直接反馈而不能直接被优化（ 虚棕线 ）。但由于反向传播算法使得小蓝猫的反馈可以被传递到小女孩那进而产生间接误差，所以与小女孩直接相连的左侧权重矩阵可以通过间接误差得到权重更新，迭代几轮，误差会降低到最小。

三、完整流程

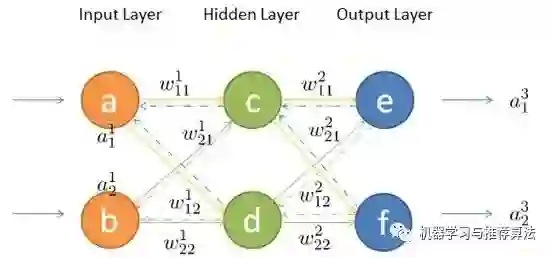
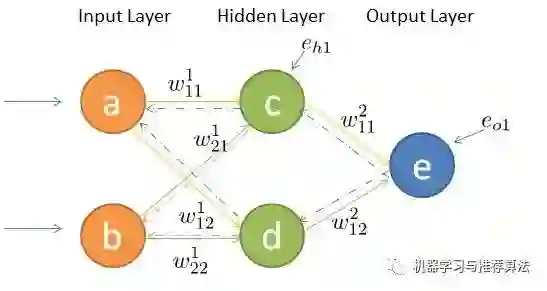
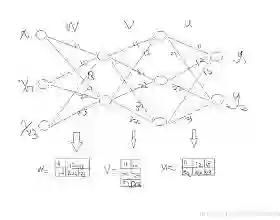
上边的栗子从直观角度了解了反向传播，接下来就详细的介绍其中两个流程前向传播与反向传播，在介绍之前先统一一下标记。

3.1 数学标记

3.2 前向传播

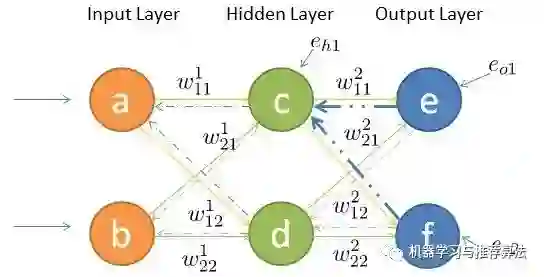
如何将输入层的信号传输至隐藏层呢，以隐藏层节点c为例，站在节点c上往后看（输入层的方向），可以看到有两个箭头指向节点c，因此a，b节点的信息将传递给c，同时每个箭头有一定的权重，因此对于c节点来说，输入信号为：

同理，节点d的输入信号为：

由于计算机善于做带有循环的任务，因此我们可以用矩阵相乘来表示：

所以，隐藏层节点经过非线性变换后的输出表示如下：

同理，输出层的输入信号表示为权重矩阵乘以上一层的输出：

同样，输出层节点经过非线性映射后的最终输出表示为：

输入信号在权重矩阵们的帮助下，得到每一层的输出，最终到达输出层。可见，权重矩阵在前向传播信号的过程中扮演着运输兵的作用，起到承上启下的功能。

3.3 反向传播

既然梯度下降需要每一层都有明确的误差才能更新参数，所以接下来的重点是如何将输出层的误差反向传播给隐藏层。

其中输出层、隐藏层节点的误差如图所示，输出层误差已知，接下来对隐藏层第一个节点c作误差分析。还是站在节点c上，不同的是这次是往前看（输出层的方向），可以看到指向c节点的两个蓝色粗箭头是从节点e和节点f开始的，因此对于节点c的误差肯定是和输出层的节点e和f有关。

不难发现，输出层的节点e有箭头分别指向了隐藏层的节点c和d，因此对于隐藏节点e的误差不能被隐藏节点c霸为己有，而是要服从按劳分配的原则（按权重分配），同理节点f的误差也需服从这样的原则，因此对于隐藏层节点c的误差为：

同理，对于隐藏层节点d的误差为：

为了减少工作量，我们还是乐意写成矩阵相乘的形式：

你会发现这个矩阵比较繁琐，如果能够简化到前向传播那样的形式就更好了。实际上我们可以这么来做，只要不破坏它们的比例就好，因此我们可以忽略掉分母部分，所以重新成矩阵形式为：

仔细观察，你会发现这个权重矩阵，其实是前向传播时权重矩阵w的转置，因此简写形式如下：

不难发现，输出层误差在转置权重矩阵的帮助下，传递到了隐藏层，这样我们就可以利用间接误差来更新与隐藏层相连的权重矩阵。可见，权重矩阵在反向传播的过程中同样扮演着运输兵的作用，只不过这次是搬运的输出误差，而不是输入信号(我们不生产误差，只是误差的搬运工(っ̯ -｡))。

四、链式求导

第三部分大致介绍了输入信息的前向传播与输出误差的后向传播，接下来就根据求得的误差来更新参数。

首先对隐藏层的w11进行参数更新，更新之前让我们从后往前推导，直到预见w11为止：

因此误差对w11求偏导如下：

求导得如下公式（所有值已知）：

同理，误差对于w12的偏导如下：

同样，求导得w12的求值公式：

同理，误差对于偏置求偏导如下：

代入上述公式为：

接着对 输入层的w11 进行参数更新，更新之前我们依然从后往前推导，直到预见第一层的w11为止（只不过这次需要往前推的更久一些）：

因此误差对输入层的w11求偏导如下：

求导得如下公式（有点长(*ฅ́˘ฅ̀*)）：

同理，输入层的其他三个参数按照同样的方法即可求出各自的偏导，在这不再赘述。

在每个参数偏导数明确的情况下，带入梯度下降公式即可（不在重点介绍）：

至此，利用链式法则来对每层参数进行更新的任务已经完成。

五、引入delta

利用链式法则来更新权重你会发现其实这个方法简单，但过于冗长。由于更新的过程可以看做是 从网络的输入层到输出层从前往后更新，每次更新的时候都需要重新计算节点的误差 ，因此会存在一些不必要的重复计算。其实对于已经计算完毕的节点我们完全可以直接拿来用，因此 我们可以重新看待这个问题，从后往前更新。先更新后边的权重，之后再在此基础上利用更新后边的权重产生的中间值来更新较靠前的参数。 这个中间变量就是下文要介绍的 delta变量 ，一来简化公式，二来减少计算量，有点动态规划的赶脚。

接下来用事实说话，大家仔细观察一下在第四部分链式求导部分误差对于输出层的w11以及隐藏层的w11求偏导以及偏置的求偏导的过程，你会发现， 三个公式存在相同的部分 ，同时隐藏层参数求偏导的过程会用到输出层参数求偏导的部分公式，这正是引入了中间变量delta的原因（其实红框的公式就是delta的定义）。

大家看一下经典书籍《神经网络与深度学习》中对于delta的描述为在第l层第j个神经元上的误差，定义为误差对于当前带权输入求偏导，数学公式如下：

因此输出层的误差可以表示为（上图红色框公式）：

隐藏层的误差可以表示为（上图蓝色框公式）：

同时对于权重更新的表示为（上图绿色框公式）：

其实对于偏置的更新表示为（上图红色框）：

上述4个公式其实就是《神经网络与深度学习》书中传说的反向传播4大公式（详细推导证明可移步此书）：

仔细观察， 你会发现BP1与BP2相结合就能发挥出最大功效，可以计算出任意层的误差，只要首先利用BP1公式计算出输出层误差，然后利用BP2层层传递，就无敌了，这也正是误差反向传播算法的缘由吧。同时对于权重w以及偏置b我们就可以通过BP3和BP4公式来计算了。

至此，我们介绍了反向传播的相关知识，一开始看反向传播资料的时候总觉得相对独立，这个教材这么讲，另一篇博客又换一个讲法，始终不能很好的理解其中的含义，到目前为止，思路相对清晰。我们先从大致流程上介绍了反向传播的来龙去脉，接着用链式求导法则来计算权重以及偏置的偏导，进而我们推出了跟经典著作一样样儿的结论，因此本人觉得较为详细，应该对初学者有一定的借鉴意义,希望对大家有所帮助。

参考资料

[1]. Nielsen M A. Neural networks and deep learning[M]. 2015.

[2]. Rashid T. Make your own neural network[M]. CreateSpace Independent Publishing Platform, 2016.

推荐阅读

[0]. 极大似然估计与最大后验概率估计

[1]. 由Logistic Regression所联想到的...

[2]. 更新！带你认识推荐系统全貌的论文清单

[3]. 当推荐系统邂逅深度学习

[4]. 在家无聊？16篇最新推荐系统论文送你

喜欢的话点个在看吧👇