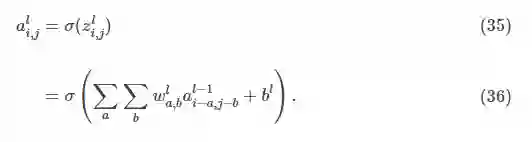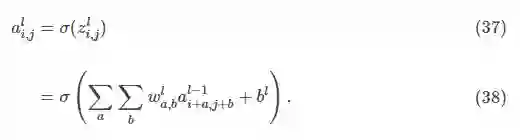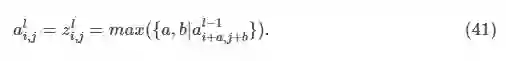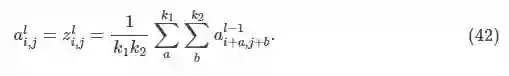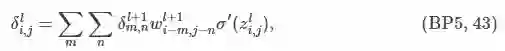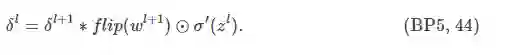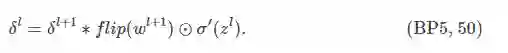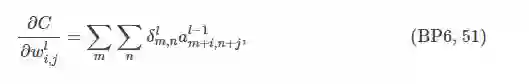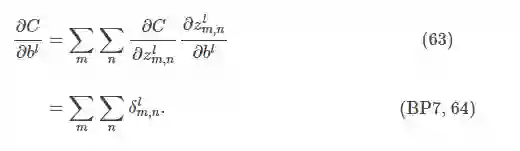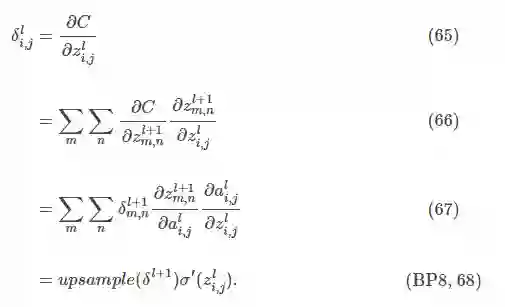误差反向传播——CNN

2018 年 7 月 12 日 统计学习与视觉计算组

1 前向传播算法

在卷积神经网络模型中，主要有三种不同类型的网络层结构：卷积层（Convolutional Layer）、池化层（Pooling Layer）、全连接层（Fully-Connected Layer）。相应地，卷积神经网络模型主要具有三个特点：局部感受野（Local Receptive Fields）、参数共享（Parameter Sharing）、池化（Pooling）。

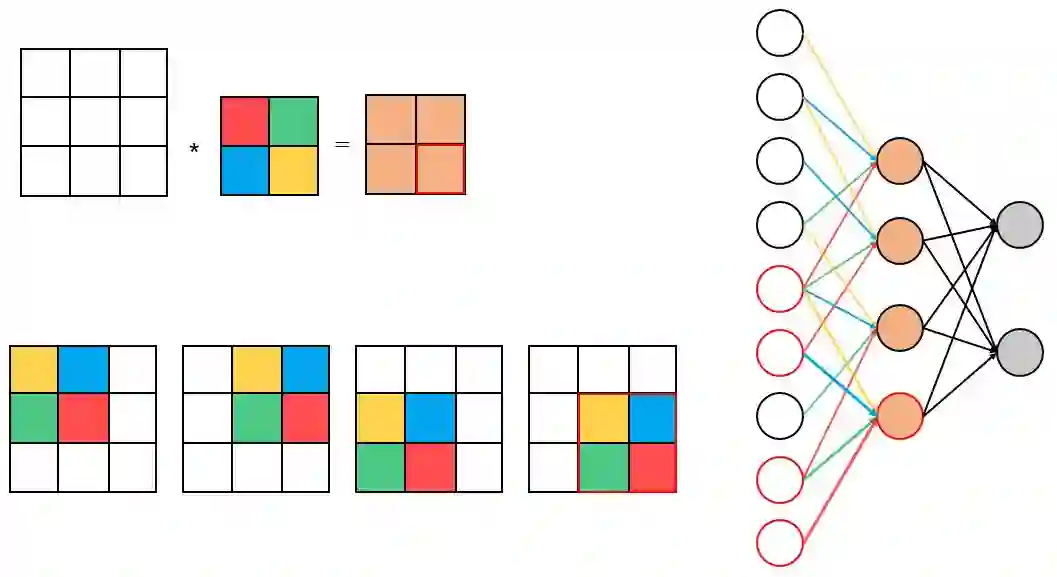
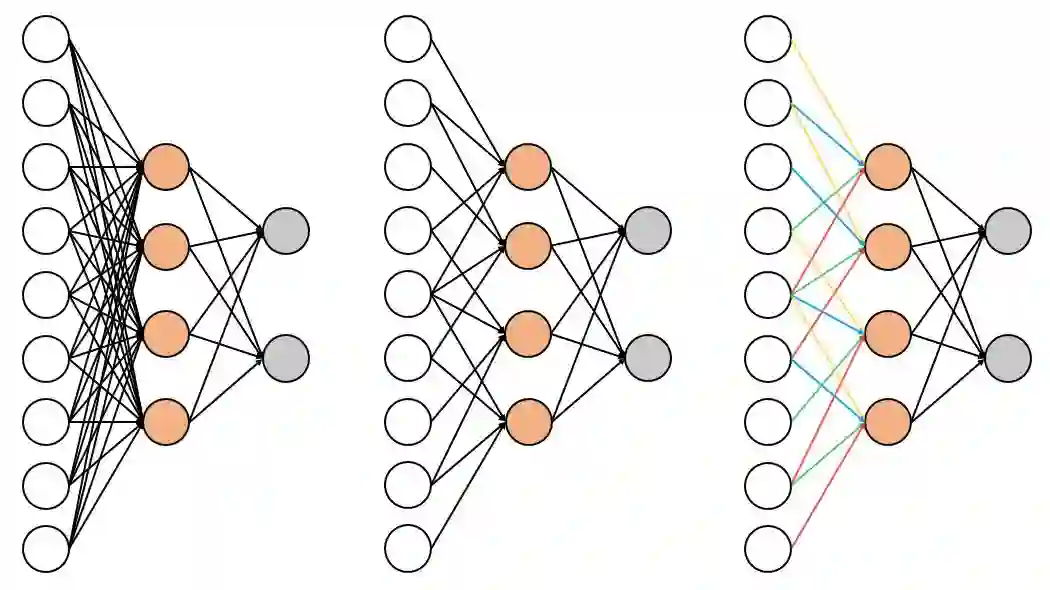
卷积神经网络模型相比于全连接神经网络模型，其保留了图像像素的空间排列信息。从神经网络模型的连接结构上看，对一个全连接层稀疏连接和共享参数，便可以把它转换为一个卷积层。下面两图形象地展示了从全连接层到卷积层的转换过程。

在卷积神经网络的前向传播过程中，不同类型的网络层结构的前向传播方式不同。下面分别说明卷积层、池化层和全连接层的前向传播过程。

1.1 卷积层的前向传播计算

下文假设步长均为 $1$ 。

卷积层的前向传播计算公式（即卷积层的卷积计算公式）为：

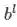
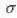
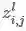
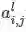
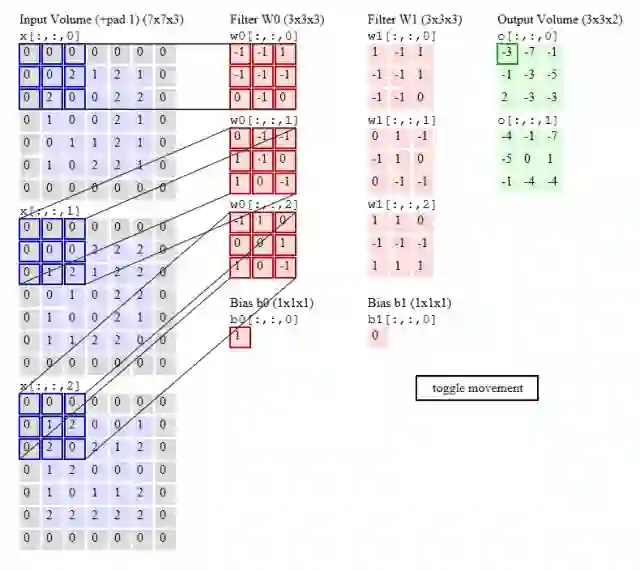
其中，为卷积核中的权重参数，为偏置参数。为卷积层节点的激活函数，为卷积层节点的输入值，为卷积层节点的激活值。

通常，在计算卷积层的前向传播结果时，往往并不会严格地遵循卷积运算，为了表述方便，往往以互相关运算取而代之。此时卷积层的前向传播计算公式为：

对比式 $(36)$ 和式 $(38)$ 可以发现，卷积运算和互相关运算的区别在于翻转卷积核，即旋转卷积核180度。矩阵表达形式的卷积层的前向传播计算公式为：

其中， $*$ 既表示卷积运算，也表示互相关运算。在本文中， $*$ 表示互相关运算。

下图形象地展示了卷积层的前向传播过程。

1.2 池化层的前向传播计算

池化层的前向传播计算比较简单。常用的池化层有最大池化层（max-pooling layer）和平均池化层（average-pooling layer）。最大池化层的前向传播计算公式为：

平均池化层的前向传播计算公式为：

从式 $(41)$ 和式 $(42)$ 可以看出，池化层没有激活函数，也没有权重参数和偏置参数。

1.3 全连接层的前向传播计算

卷积神经网络的全连接层和全连接神经网络的全连接层一样，具体公式参见上一篇《误差反向传播——MLP》。

2 误差反向传播算法

在卷积神经网络的误差反向传播过程中，不同类型的网络层结构的反向传播方式不同。卷积神经网络的节点误差定义和全连接神经网络的相同 $(7)$ 。下面分别说明卷积层、池化层和全连接层的误差反向传播过程。

2.1 卷积层的误差反向传播计算

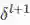
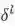
即已知卷积层的误差，反向传播计算上一层的误差。

通过第 $l + 1$ 层第 $(i, j)$ 个节点误差值计算第 $l$ 层第 $(i, j)$ 个节点误差值的节点误差公式为：

即，

证明：
应用复合函数的链式法则，证明如下：

根据式 $(36)$ 和式 $(38)$ ，以及卷积运算的可交换性可知：

证毕。

已知当前层的节点误差，则第 $l$ 层第 $(i, j)$ 个卷积核节点的权重梯度公式为：

即，

证明：
应用复合函数的链式法则，证明如下：

根据式 $(38)$ 可知：

证毕。

因为每一个卷积核只有一个共享的偏置参数，所以第 $l$ 层的偏置梯度公式为：

2.2.2 池化层的误差反向传播计算

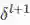
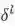
即已知池化层的误差，反向传播计算上一层的误差。

通过第 $l + 1$ 层第 $(i, j)$ 个节点误差值计算第 $l$ 层第 $(i, j)$ 个节点误差值的节点误差公式为：

对于最大池化层，根据式 $(41)$ 可以将上一层各个子区域中最大的激活值的权重视为 $1$ ，其余的激活值的权重视为 $0$ 。此时最大池化层和卷积层的误差反向传播过程相同，但在最大池化层的前向传播过程中需要记录各个子区域中最大的激活值的位置。

同样地，对于平均池化层，根据式 $(42)$ 可以将上一层各个子区域中的权重视为该子区域的节点总数的倒数。此时平均池化层和卷积层的误差反向传播过程相同。

矩阵的表达形式为：

由于池化层没有权重参数和偏置参数，即其权重参数和偏置参数均为常量，因此池化层的权重梯度和偏置梯度均为 $0$ 。

2.2.3 全连接层的误差反向传播计算

卷积神经网络的全连接层和全连接神经网络的全连接层一样，具体的计算公式参见上一篇《误差反向传播——MLP》。

参考博客：

1.http://neuralnetworksanddeeplearning.com/chap1.html
2.http://neuralnetworksanddeeplearning.com/chap2.html
3.http://cs231n.github.io/convolutional-networks/
4.https://grzegorzgwardys.wordpress.com/2016/04/22/8/
5.https://blog.csdn.net/hearthougan/article/details/72910223

登录查看更多