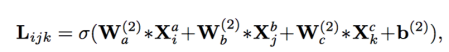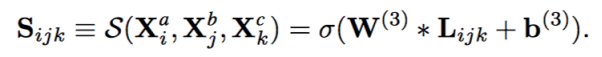网络节点表示学习论文笔记01—AAAI2018超网络节点表示学习

2018 年 2 月 9 日 专知专知内容组（编）

【导读】近日，针对在真实世界网络数据中存在的超边的问题，也就是说节点关系经常超出成对关系的范围，来自清华大学与康奈尔大学的研究者发表论文提出了“深度超网络嵌入”（Deep Hyper-Network Embedding, DHNE）模型去对含有不可分超边的超网络的节点向量表示。文章证明了现有方法使用的嵌入空间中常见的线性相似性度量不能维持超网络的不可分属性，在此基础上提出的深度模型，可以在保护嵌入空间内，建立起局部与全局邻近区域的非线性元组相似性函数。在四个不同种类的超网络上做了大规模的实验，包括一个GPS网络、一个在线社交网络、一个药物网络和一个语义网络，文中方法可以在保证稳定性的前提下显著优于现有的算法。

【论文】：Structural Deep Embedding for Hyper-Networks

论文链接：

https://arxiv.org/abs/1711.10146

▌摘要

网络嵌入（network embedding）最近在数据挖掘领域吸引了大量的关注。已有的网络嵌入方法主要关注于成对关系的网络（networks with pairwise relationships）。然而，在真实世界中，数据中的关系经常超出成对关系的范围。例如：三个或者更多对象被超边关联在一起，组成一个超网络。当超边不可分解时（任何超边中节点的子集无法组成另一个超边），这些超网络给已有的网络嵌入方法带来了很大的挑战。尤其是，这些不可分解的超边常见于异构网络中。

这篇文章中，我们提出了一个新颖的“深度超网络嵌入”（Deep Hyper-Network Embedding, DHNE）模型去对含有不可分超边的超网络做嵌入。特别指出，理论上我们证明了现有方法使用的嵌入空间中常见的线性相似性度量不能维持超网络的不可分属性，因此，提出了一个新的深度模型，去体现保护嵌入空间内，局部与全局邻近区域的非线性元组相似性函数。

我们在四个不同种类的超网络上做了大规模的实验，包括一个GPS网络、一个在线社交网络、一个药物网络和一个语义网络。结果表明，我们的方法可以在保证稳定性的前提下显著优于现有的算法。

▌介绍

如今，在多个领域内，网络被广泛的用于表示富关系的数据对象，构成了诸如社交网络、生物网络、脑网络等网络结构。为了分析网络，许多方法被提出来，其中网络嵌入方法在近年引起了越来越多的兴趣。大多数已有的算法多是为了传统成对网络（一条边只连接两个节点对）设计。然而，在真实世界应用中，数据对象中的关系比成对网络更加复杂。例如，约翰采购了一件棉质衬衫，这一行为组成了一个高阶关系<约翰，衬衫，棉花>。那些刻画了高阶节点关系的网络通常被称为一个超网络。

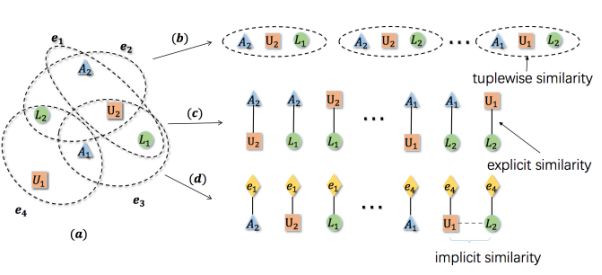
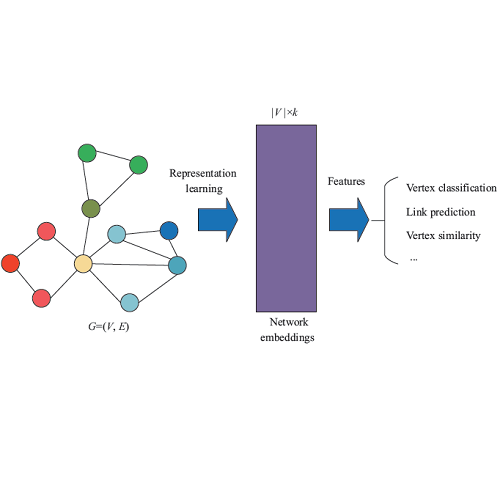
图：（a）超网络的例子；（b）提出的方法；（c）群体扩展；（d）标注扩展。

提出的方法将超网络建模为一个整体，同时，元组相似性得到了保护。在群体扩展中，每个超边被扩展为一个群体，每个节点对被显示的标识为相似。在标注扩展中，超边中的每个节点均连接与一个代表原始超边的节点上。原始超边中的每个节点均连接到一个相同的节点上，形成隐式相似。

典型的分析超网络的方法是：先将其扩展为一个传统成对网络，进而使用为成对网络设计的算法去分析。为达到这一目标，设计了小团体扩展（clique expansion）与标注扩展（star expansion）两种表示技术。在集团扩充中，每一个超边被扩展为一个群体。在标注扩展中，一个超图被转换为一个二分图，每条超边被一个实例节点（连接到它所容纳的原始节点）表示。这些方法均假设超边是可分解的，这意味着，当面对一个超边时，其中任何一组节点子集均可组成另一个超边。在同构超网络中的大多数例子中，由于同构网络中包含的对象潜在相关，因此这个假设是有道理的。但是为了学习异构网络嵌入，需要达到如下要求：

1、 不可分：异构超网络中的超边通常是不可分的。在这个例子中，超边中一组节点有很强的关联关系（节点子集并不强相关）。例如，在推荐系统中，包含了<用户，电影，标签>关系，而<用户，标签>的关系并不是非常强。这意味着我们不能简单的使用那些传统扩展方法分解超边。

2、 结构维护：在网络嵌入中，局部结构被观察到的关系维护着。然而，由于网络的稀疏性，有许多已有的关系并未被观察到。仅使用局部结构无法满足超网络的维护。并且全局结构（如邻居结构，neighborhood structure），被要求针对于这类稀疏问题。如何同时捕获与维护超网络中的局部与全局结构仍然是一个未解决的问题。

为了解决不可分问题，作者设计了一个不可分的元组相似性函数，这个函数直接定义与超边上的全体节点，确保任何超边的子集没有被包含在网络嵌入中。本文理论上证明了不可分的远足相似性函数不能是线性函数，因而，本文通过在深度神经网路上增加非线性激活函数的方法实现了高非线性（highly non-linear）。为了解决结构保护问题，作者设计了一个深度自编码器通过重建临近结构去学习网络节点表示，保证了邻近的节点映射到相似的嵌入空间中。使用元组相似性函数与自动编码器同时联合优化以解决这两个问题。

文章的贡献如下：

1、研究了不可分超网络嵌入的问题，在超网络中，超边是一个常见的属性，但却被文献大量忽略。作者提出了一个新颖的深度模型，命名为深度超网络嵌入（Deep Hyper-Network Embedding, DHNE），用来学习那些异构超网络的嵌入的问题，这一模型可以同时在保护富结构信息的前提下解决超边不可分的问题。这个方法的复杂度相对于节点个数是线性的，因此可以应用于大规模网络中。

2、本文理论上证明了在超网络的嵌入空间中任何线性相似性度量都不能保持不可分属性，因此提出了一个新颖的深度模型，以同时保持超网络的局部与全局的结构不可分信息。

3、本文在四个真实世界信息网络中做了相关实验。结果证明了本文模型的效率与有效性。

▌主要方法：

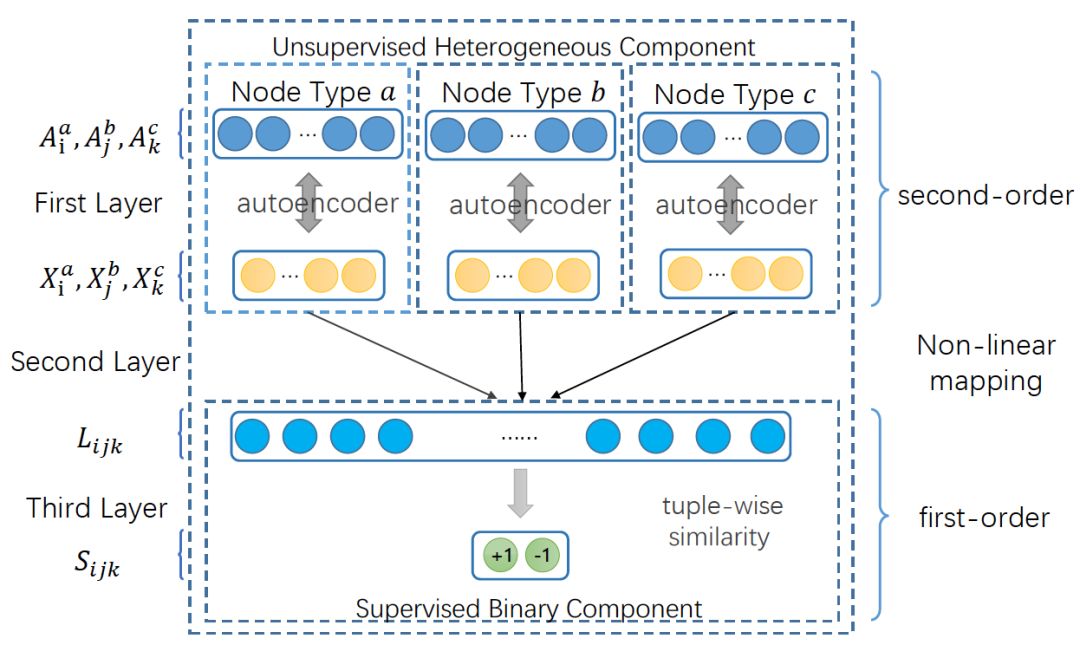
前面讲到在异质网络中要解决两个问题：不可分解性和结构保留。对于不可分解性，作者设计了不可分解的tuplewise相似性函数。这个相似性函数定义在hyper edge的所有节点上，确保超边的子集并没有融合在网络表示中，并且这个函数是非线性的。为了保留网络结构，作者设计了一个 Autoencoder，通过重构节点的邻居结构来学习节点表示，也就说有相似邻居的节点将有相似的向量表示，每一种节点类型对应一个autoencoder。这两部分在模型中，联合优化来同时解决这两个问题。模型框架图如下：

图是深度超网络嵌入框架

于一阶相似性，本文采用的是multilayer perceptron，分成两个部分。第一部分是模型框架中的第二层，这是个全连接层而且激活函数是非线性的。输入是三个节点(vi,vj,vk)（他们属于三个不同的节点类型a,b,c）的向量表示(Xai,Xbj,Xck)。作者把他们拼接起来，并且映射到统一的空间L。

为了得到相似性，把它统一的空间中的表示Lijk映射到第三层的概率空间中：

如果节点(vi,vj,vk)之间存在hyper edge，那么Rijk的值为1，否则为0。损失函数：

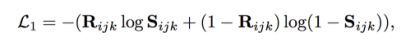
Auto Encoder的目的就是最小化输入和输出的重构错误。这就使得有相似邻居结构的节点，向量表示相近，也就是保留了二阶相似性。邻接矩阵往往是稀疏的，因而作者只是处理非零项，通过sign函数。此外，每个节点类型对应着一个Auto encoder，因而损失函数是：

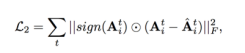
为了保留一阶和二阶相似性，论文联合最小化目标函数：

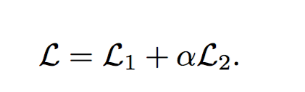
在大多数现实世界的网络中只有正相关关系，所以这个算法收敛时，其中所有的元组关系都是相似的。为了解决这个问题，根据噪声分布，为每条边采样多个负边。整体算法如下：

▌实验结果

在实验方面，作者用了四个数据集：

1. GPS：超边是（user, location, activity）

2. MovieLens：超边是（user, movie, tag）

3. drug：超边是（user, drug, reac- tion）

4. WordNet：超边是（entity, relation, tail entity）

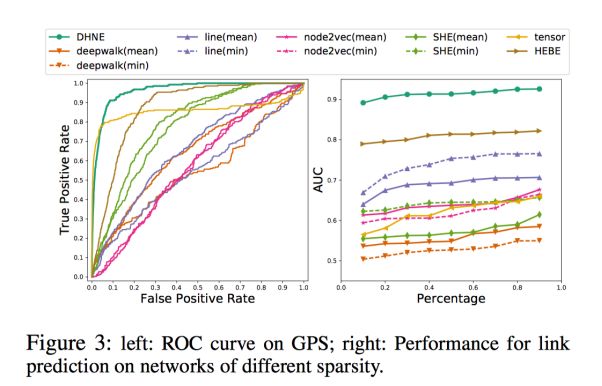
左：GPS网络中的ROC曲线；右：不同稀疏的连接预测性能

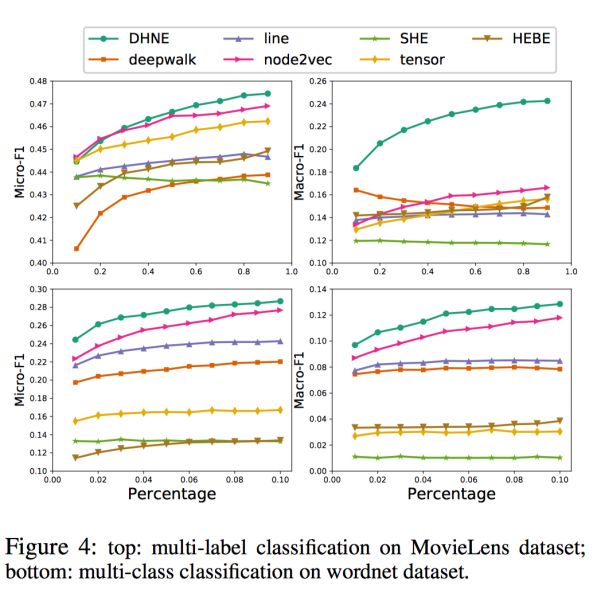
图中：上：MovieLens数据集上的多标签分类问题；下：wordnet数据集上的多分类问题。

▌结论

本文提出了一个名为DHNE的深度模型，去学习具有不可分超边的超网络结构的低维表示。特别的，本文理论证明了在现有方法中使用的线性相似性度量，无法在嵌入空间中继续保持超网络的不可分属性。因此，提出了一个新的深度模型去表示一个非线性元组相似方法，在嵌入空间中同时保护了局部与全局的临近结构特征。在四个不同类型的超网络中做了大量的实验，包括一个GPS网络，一个在线社交网络，一个药物网络，以及一个语义网络。结果证明了提出的方法可以在兼顾稳定和效率的情况下超越现有方法。

参考链接：

https://arxiv.org/abs/1711.10146

-END-

专 · 知

人工智能领域主题知识资料查看获取：【专知荟萃】人工智能领域26个主题知识资料全集（入门/进阶/论文/综述/视频/专家等）

同时欢迎各位用户进行专知投稿，详情请点击：

【诚邀】专知诚挚邀请各位专业者加入AI创作者计划！了解使用专知！

请PC登录www.zhuanzhi.ai或者点击阅读原文，注册登录专知，获取更多AI知识资料！