神经网络的准确率和鲁棒性不能兼得?不,让我们来仔细看看

极市导读
针对目前对抗攻击领域存在的一个痛点问题:神经网络鲁棒性的提升会伴随着准确率的下降,本文提出了一个新的研究视角。从数据集的内在属性出发,发现神经网络在一定条件下可以兼顾准确率和鲁棒性。此外,作者研究了现有模型的准确率和鲁棒性无法相互协调的原因,并提出了有效的解决方案。>>就在明天,郑哲东:从行人重识别到无人机定位,重识别领域最强技术分享!

论文:A Closer Look at Accuracy vs. Rubustness(NeuIPS2020)
论文地址:https://arxiv.org/abs/2003.02460
论文代码:https://github.com/yangarbiter/robust-local-lipschitz
引言
大量研究表明神经网络极易受到对抗样本的攻击——输入样本上的微小扰动就能让其预测错误。尽管目前已经涌现出许多抵御对抗攻击的方法,但这些方法一般都会造成模型准确率的下降。因此,大部分前人工作认为在分类任务上,必须对模型的准确率和鲁棒性做一个折衷,两者是无法兼得的。本文针对这个问题进行了进一步研究,发现真实图像数据集一般是可划分的,而利用数据集的可划分属性,神经网络模型在一定条件下可以同时满足高准确率和强鲁棒性两个要求。
论文贡献
该论文的贡献可以总结为以下三点:
-
作者通过实验证明了常用的真实图像数据集是自然可划分的。
-
基于数据集的可划分属性,作者在理论上证明了利用局部利普西斯函数,神经网络模型可以同时具有高准确率和强鲁棒性,打破了以往认为两者不能兼得的认知局限。
-
作者研究了现有训练方法产生的分类器的平滑性和泛化差距(训练集和测试集准确率的差距),发现一些能够产生鲁棒分类器的训练方法,依然无法缓解模型具有很大泛化差距的问题。因此,作者提出将dropout技术应用到这些训练方法中来缩小模型的泛化差距,本文实验结果证明了该方法的有效性。
模型介绍
一、预备知识
鲁棒性和机敏性(astuteness):令 表示以 为中心,半径为 的球, 若对于任意的 ,都有 ,则称分类器 是鲁棒的。此外,若对于任意的 ,都有 , 是样本 的真实标签,则称分类器 是机敏的。
也就是说,模型的机敏性是对其鲁棒性和准确率的一个综合考量,因此我们的目标也就是获得具有高机敏性的模型 [1]。
局部利普西斯性(Local Lipschitzness):给定样本输入空间 和一个距离度量函数 , 表示所有标签的集合,则函数 的局部利普西斯性定义为:
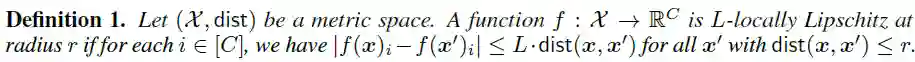
这里 表示 的第 个元素。
当两个样本 和 的距离度量不超过 时,若对于所有的类别 ,都有 ,则称函数 满足 - 。
可划分性(Seperation):假设输入空间 包含 个互不相交的子集 ,每个子集 中的样本的标签都是 ,则称满足如下定义的数据分布是 -可分的( -reparation):
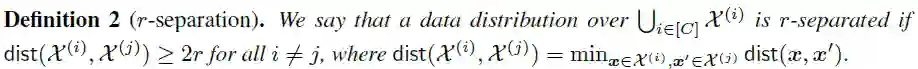
该性质要求具有 -可分性的数据集中,任何两个具有不同标签的样本 和 ,它们之间的距离度量至少为 。
二、真实图像数据集的 -可分性
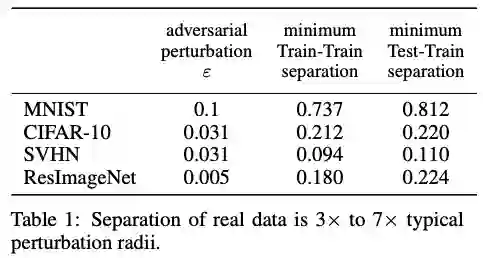
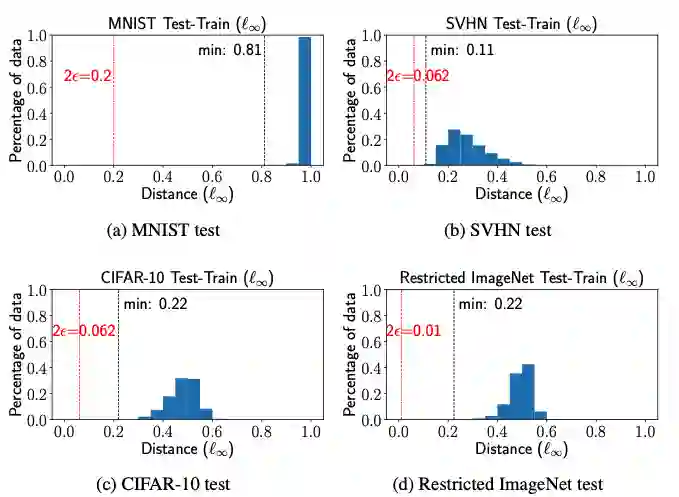
在这里,作者通过实验验证四种经常使用的真实图像数据集是否具有 -可分性。如下图所示:
这里距离度量函数 选为 距离, 表示每种数据集在对抗样本实验中常用的扰动半径大小,Train-Train separation表示每个训练样本和离它最近的且具有不同标签的训练样本之间的 距离,Test-Train separation表示每个测试样本和离它最近的且具有不同标签的训练样本之间的 距离。我们可以发现,Train-Train和Test-Train separation都要大于对抗扰动半径 的2倍,由 -separation的定义可知,这些数据集至少是 -可分的。
三、 -可分数据集的鲁棒性和准确率
作者从理论上证明了如果数据分布是 -可分的,那么利用局部利普西斯函数,一定存在一个既鲁棒同时准确率又高的模型。具体的证明如下:
已知函数 将输入 映射为一个C维实向量 :
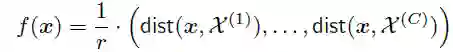
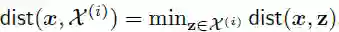
表示样本 和标签为 的所有样本间的最小距离,
故 。
然后定义分类器 为:
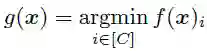
也就是说分类器 将输入样本 预测为距离它最近的样本所属的类别 。
于是作者给出如下引理:

若函数 在 周围半径为 的区域 内满足 - ,并且对于任何非真实标签 的维度 ,都有 ,则上述定义的分类器 在 周围半径为 的区域内可以达到100%的分类准确率,即一定有 ,也就是说 是足够机敏的(astute),实现了鲁棒性和准确率的双赢。
证明过程如下:
由上文局部利普西斯性的定义可知,若函数 满足 - ,
则当 时,有
,
又因为对于任意的 ,
都有 ,
所以可得如下不等式:
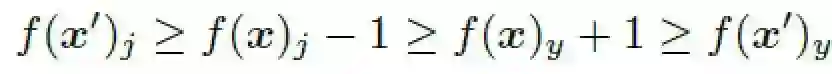
因此当 时, ,即分类器 一定会预测正确。
作者在论文中进一步证明了当数据集具有 -可分性时,一定存在满足上述引理的函数 和具有 准确率的分类器 ,具体细节可参考原文。
实验结果
上文在理论上证明了模型的准确率和鲁棒性两者可以兼得(即足够机敏),但是实际中大部分模型的准确率和鲁棒性两者之间往往不能互相协调,于是作者通过实验研究这种现象背后的可能原因,并进一步提出可行的方法来缓解这个问题。
在本文中,作者主要通过两个方面来对神经网络模型进行分析,分别是(1)现有训练方法产生的模型的局部利普西斯性(前人工作曾表明模型的利普西斯性和鲁棒性紧密相关),(2)这些模型的泛化能力。
作者通过如下公式定义利普西斯常数来评估模型的局部利普西斯性:
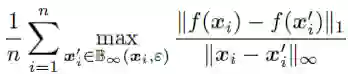
利普西斯常数越小,表示模型越平滑。
而模型的泛化能力则用模型在训练集和测试集上准确率的差距来评估。
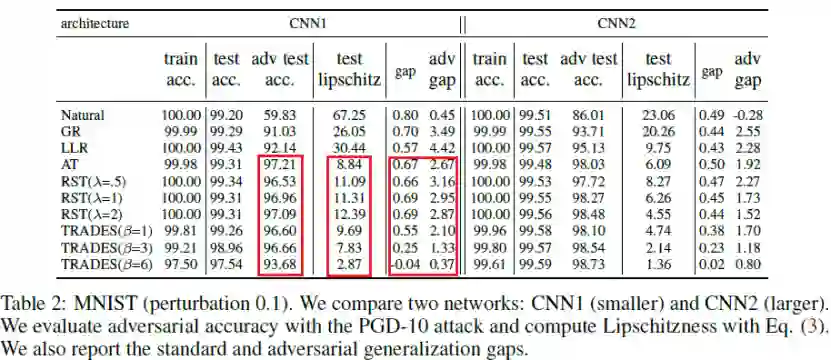
上表显示了两种卷积神经网络在不同的训练方法Natural, GR, LLR, AT, RST, TRADES下的性能,包括在训练集上的准确率,在测试集上的准确率,在测试集对抗样本上的准确率(简称为对抗准确率),利普西斯常数,训练集和测试集准确率的差,训练集和测试集对抗准确率的差。我们发现(1)模型的利普西斯性和其对抗准确率密切相关,比如鲁棒的训练方法AT,RST,TRADES的利普西斯性比Natural, GR, LLR好(即利普西斯常数更小),它们的对抗准确率也较高;(2)尽管模型具有较小的利普斯西常数,更加平滑,但它们在训练集和测试集上的泛化差距依然很大。
因此,作者提出采用经典的dropout技巧来缩小模型的泛化差距。如下图所示,
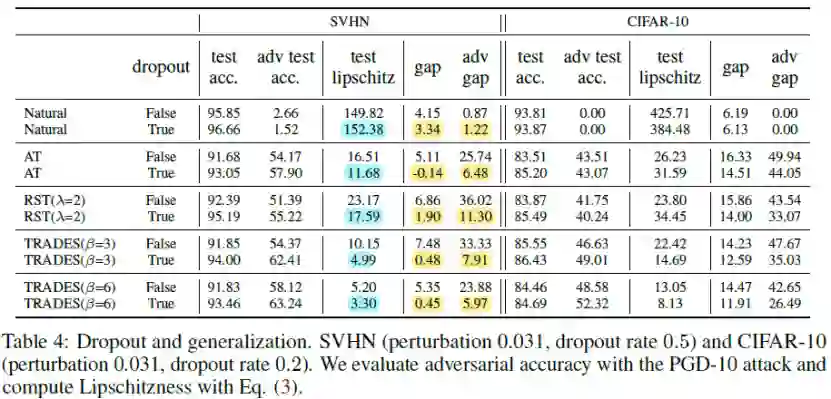
可以看到,加了dropout的模型具有更小的泛化差距,同时模型变得更加平滑,利普西斯常数更小,而测试准确率和对抗准确率均有明显的提升,说明dropout能够有效提升模型的泛化能力和局部利普西斯性。
参考:
[1] Yizhen Wang, Somesh Jha, and Kamalika Chaudhuri. Analyzing the robustness of nearest neighbors to adversarial examples. In International Conference on Machine Learning, pages 5133--5142, 2018.
推荐阅读