ICML'21 | 7篇GNN的可解释性与扩展性

国际机器学习大会（ International Conference on Machine Learning, ICML）是由国际机器学习学会（IMLS）主办的年度机器学习国际顶级会议，今年论文接收率为21.48％。今天为大家带来ICML 2021四篇关于图神经网络可解释性的文章以及两篇关于图神经网络扩展性的文章分享。

1研究背景

可解释性是人工智能的一个关键部分，因为它可以实现可靠和可信的预测。深度学习模型由于其“黑箱”特性被人广为诟病，并进一步阻碍了其应用。近年来，深度学习模型的可解释性研究在图像和文本领域取得了显著进展。然而，由于图结构的不规则性，将现有的解释方法应用于图神经网络存在着巨大的挑战。尽管如此，图神经网络的可解释性是目前比较值得探索的方向之一。

此外，阻碍图神经网络在实际场景中进一步广泛应用的一大挑战是模型的扩展性(Scalability)问题。在工业级业务场景，尤其是互联网公司的业务场景，图网络规模通常都很大，至少包含亿级，甚至是十亿级、百亿级的图节点和边。现有的大多数研究都集中在开发新的图神经网络模型，并在小图上进行测试（例如一些Cora和Citeseer等仅有几千个节点的引文网络数据集），而忽视了实际的应用挑战。图神经网络难以应用到大规模图数据的主要原因是在图神经网络的消息传递过程中，节点的最终状态涉及其大量近邻节点的隐藏状态，导致反向传播变得非常复杂。虽然有些方法试图通过快速采样和子图训练来提升模型效率，但它们仍无法扩展到大型图的深度架构上。

今年ICLR收录了四篇关于图神经网络可解释性的文章以及两篇关于图神经网络扩展性的文章，以下是今天的分享。

2Explainability (可解释性问题)

2.1On Explainability of Graph Neural Networks via Subgraph Explorations

作者：Hao Yuan, Haiyang Yu, Jie Wang, Kang Li, Shuiwang Ji
单位：Texas A&M, 中科大等
论文链接：http://proceedings.mlr.press/v139/yuan21c.html
代码链接：https://github.com/divelab/DIG

Highlight: In this work, we propose a novel method, known as SubgraphX, to explain GNNs by identifying important subgraphs.

2.2Generative Causal Explanations for Graph Neural Networks

作者：Wanyu Lin, Hao Lan, Baochun Li
单位：香港理工大学, 多伦多大学等
论文链接：http://proceedings.mlr.press/v139/lin21d.html

Highlight: This paper presents Gem, a model-agnostic approach for providing interpretable explanations for any GNNs on various graph learning tasks.

2.3Improving Molecular Graph Neural Network Explainability with Orthonormalization and Induced Sparsity

作者：Ryan Henderson, Djork-Arné Clevert, Floriane Montanari
单位：Bayer AG
论文链接：http://proceedings.mlr.press/v139/henderson21a.html

Highlight: To help, we propose two simple regularization techniques to apply during the training of GCNNs: Batch Representation Orthonormalization (BRO) and Gini regularization.

2.4Explainable Automated Graph Representation Learning with Hyperparameter Importance

作者：Xin Wang, Shuyi Fan, Kun Kuang, Wenwu Zhu
单位：清华大学，浙江大学
论文链接：http://proceedings.mlr.press/v139/wang21f.html

Highlight: We propose an explainable AutoML approach for graph representation (e-AutoGR) which utilizes explainable graph features during performance estimation and learns decorrelated importance weights for different hyperparameters in affecting the model performance through a non-linear decorrelated weighting regression.

3Scalability (扩展性问题)

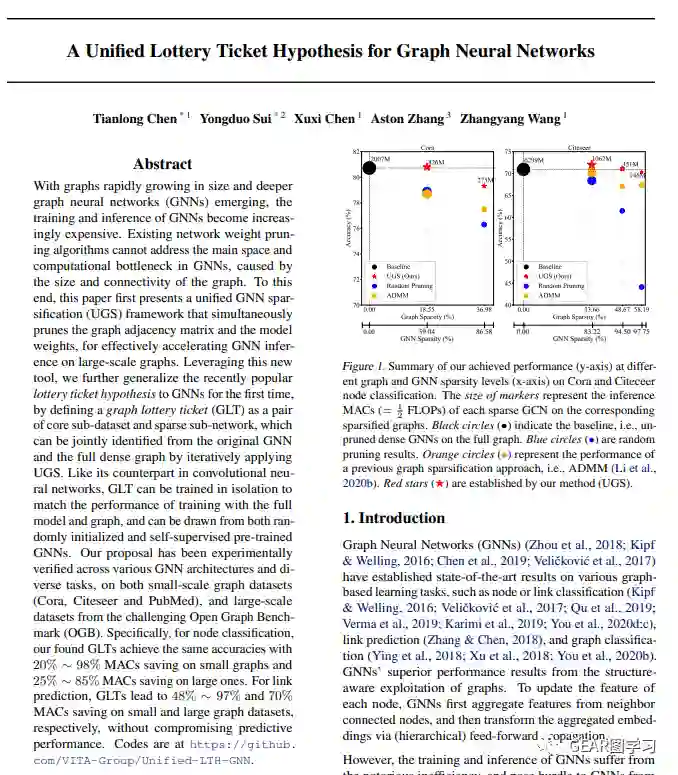
3.1A Unified Lottery Ticket Hypothesis for Graph Neural Networks

作者：Tianlong Chen, Yongduo Sui, Xuxi Chen, Aston Zhang, Zhangyang Wang
单位：University of Texas，中科大等
论文链接：http://proceedings.mlr.press/v139/chen21p.html
代码链接：https://github.com/VITA-Group/Unified-LTH-GNN

Highlight: To this end, this paper first presents a unified GNN sparsification (UGS) framework that simultaneously prunes the graph adjacency matrix and the model weights, for effectively accelerating GNN inference on large-scale graphs. Leveraging this new tool, we further generalize the recently popular lottery ticket hypothesis to GNNs for the first time, by defining a graph lottery ticket (GLT) as a pair of core sub-dataset and sparse sub-network, which can be jointly identified from the original GNN and the full dense graph by iteratively applying UGS.

3.2GNNAutoScale: Scalable and Expressive Graph Neural Networks via Historical Embeddings

作者：Matthias Fey, Jan E. Lenssen, Frank Weichert, Jure Leskovec
单位：TU Dortmund University, Stanford University
论文链接：http://proceedings.mlr.press/v139/fey21a.html
代码链接：https://github.com/rusty1s/pyg_autoscale

Highlight: We present GNNAutoScale (GAS), a framework for scaling arbitrary message-passing GNNs to large graphs.

本期编辑：李金膛
审核：陈亮