近期必读的六篇顶会 ICML 2020【图神经网络 (GNN) 】相关论文

【导读】ICML(International Conference on Machine Learning)，即国际机器学习大会, 是机器学习领域全球最具影响力的学术会议之一，因此在该会议上发表论文的研究者也会备受关注。因疫情的影响, 今年第37届ICML大会将于2020年7月13日至18日在线上举行。据官方统计，ICML 2020共提交4990篇论文，接收论文1088篇，接收率为21.8%。与往年相比，接收率逐年走低。在会议开始前夕，专知小编为大家整理了ICML 2020图神经网络（GNN）的六篇相关论文供参考——核GNN、特征变换、Haar 图池化、无监督图表示、谱聚类、自监督GCN。

ICML 2020 Accepted Papers https://icml.cc/Conferences/2020/AcceptedPapersInitial

ACL2020GNN_Part1、WWW2020GNN_Part1、AAAI2020GNN、ACMMM2019GNN、CIKM2019GNN、ICLR2020GNN

1. Convolutional Kernel Networks for Graph-Structured Data

作者：Dexiong Chen, Laurent Jacob, Julien Mairal

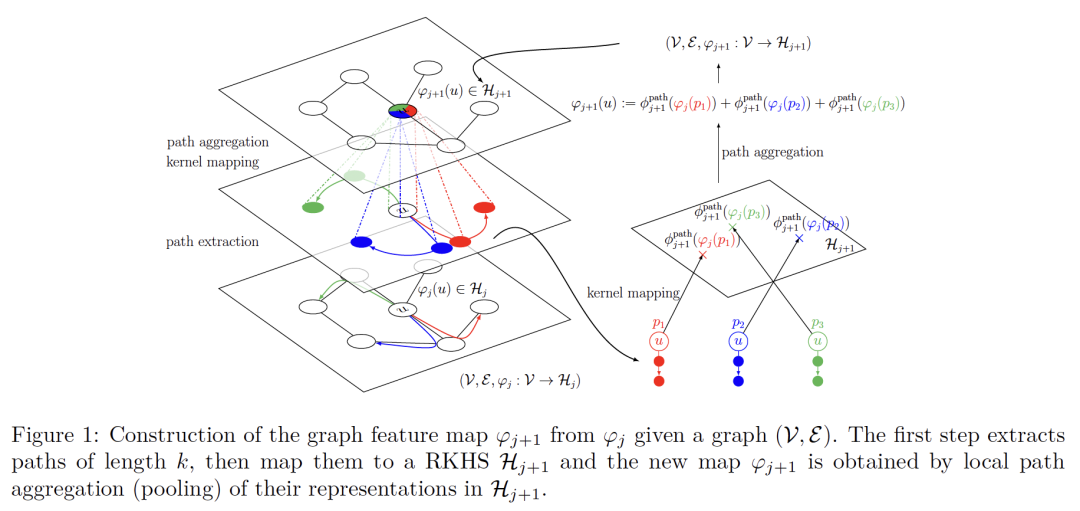
摘要：我们引入了一系列多层图核，并在图卷积神经网络和核方法之间建立了新的联系。我们的方法通过将图表示为核特征映射序列将卷积核网络推广到图结构数据，其中每个节点携带关于局部图子结构的信息。一方面，核的观点提供了一种无监督的、有表现力的、易于正规化的数据表示，这在样本有限的情况下很有用。另一方面，我们的模型也可以在大规模数据上进行端到端的训练，从而产生了新型的图卷积神经网络。我们的方法在几个图分类基准上取得了与之相当的性能，同时提供了简单的模型解释。

网址： https://arxiv.org/abs/2003.05189

代码链接： https://github.com/claying/GCKN

2. GNN-FILM: Graph Neural Networks with Feature-Wise Linear Modulation 作者：Marc Brockschmidt

摘要：本文提出了一种新的基于特征线性调制（feature-wise linear modulation，FiLM）的图神经网络(GNN)。许多标准GNN变体仅通过每条边的源的表示来计算“信息”，从而沿着图的边传播信息。在GNN-FILE中，边的目标节点的表示被附加地用于计算可以应用于所有传入信息的变换，从而允许对传递的信息进行基于特征的调制。基于基线方法的重新实现，本文给出了在文献中提到的三个任务上的不同GNN体系结构的实验结果。所有方法的超参数都是通过广泛的搜索找到的，产生了一些令人惊讶的结果：基线模型之间的差异比文献报道的要小。尽管如此，GNN-FILE在分子图的回归任务上的表现优于基线方法，在其他任务上的表现也具有竞争性。

网址： https://arxiv.org/abs/1906.12192

3. Haar Graph Pooling

作者：Yu Guang Wang, Ming Li, Zheng Ma, Guido Montufar, Xiaosheng Zhuang, Yanan Fan

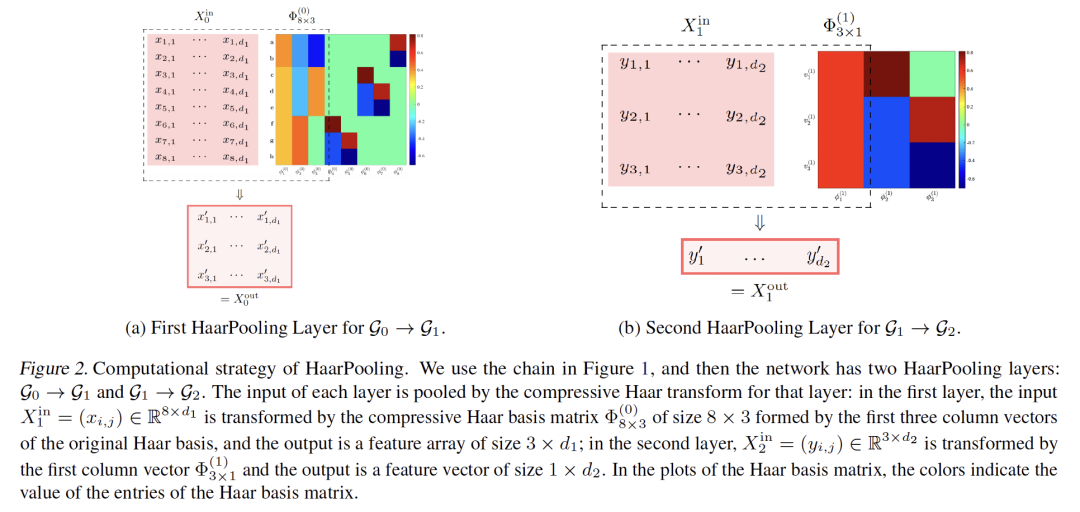
摘要：深度图神经网络(GNNs)是用于图分类和基于图的回归任务的有效模型。在这些任务中，图池化是GNN适应不同大小和结构的输入图的关键因素。本文提出了一种新的基于压缩Haar变换的图池化操作-HaarPooling。HaarPooling实现了一系列池化操作；它是通过跟随输入图的一系列聚类序列来计算的。HaarPooling层将给定的输入图变换为节点数较小、特征维数相同的输出图；压缩Haar变换在Haar小波域中过滤出细节信息。通过这种方式，所有HaarPooling层一起将任何给定输入图的特征合成为大小一致的特征向量。这种变换提供了数据的稀疏表征，并保留了输入图的结构信息。使用标准图卷积层和HaarPooling层实现的GNN在各种图分类和回归问题上实现了最先进的性能。

网址： https://arxiv.org/abs/1909.11580

4. Interferometric Graph Transform: a Deep Unsupervised Graph Representation 作者：Edouard Oyallon

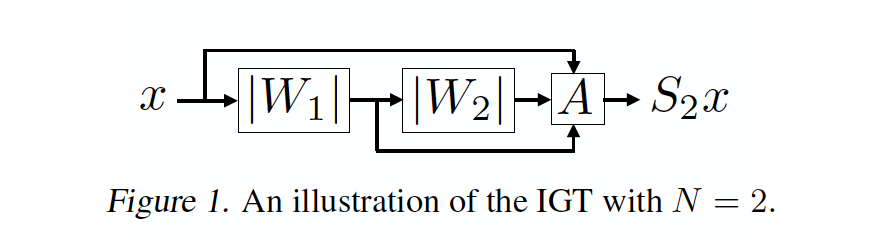
摘要：我们提出了Interferometric Graph Transform(IGT)，这是一类用于构建图表示的新型深度无监督图卷积神经网络。我们的第一个贡献是提出了一种从欧几里德傅立叶变换的推广得到的通用复数谱图结构。基于一个新颖的贪婪凹目标，我们的学习表示既包括可区分的特征，也包括不变的特征。通过实验可以得到，我们的学习过程利用了谱域的拓扑，这通常是谱方法的一个缺陷，特别是我们的方法可以恢复视觉任务的解析算子。我们在各种具有挑战性的任务上测试了我们的算法，例如图像分类(MNIST，CIFAR-10)、社区检测(Authorship，Facebook graph)和3D骨架视频中的动作识别(SBU，NTU)，在谱图非监督环境下展示了一种新的技术水平。

网址：

https://arxiv.org/abs/2006.05722

5. Spectral Clustering with Graph Neural Networks for Graph Pooling

作者：Filippo Maria Bianchi, Daniele Grattarola, Cesare Alippi

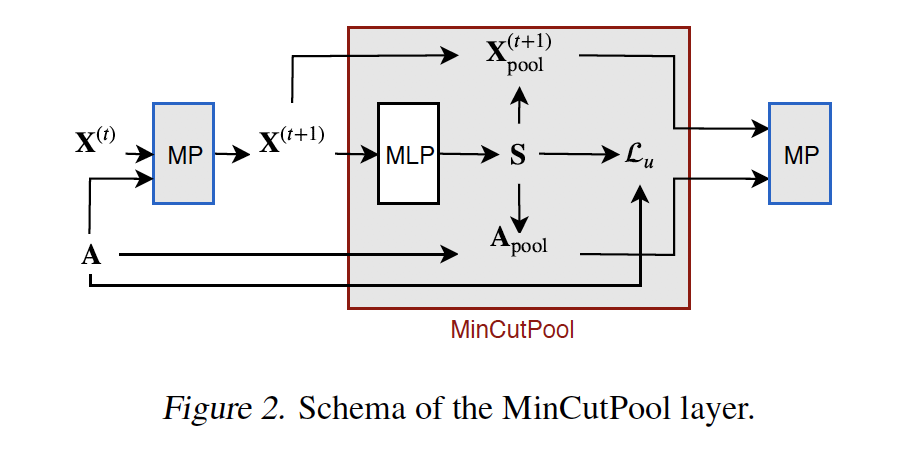
摘要：谱聚类(SC)是发现图上强连通社区的一种流行的聚类技术。SC可以在图神经网络(GNN)中使用，以实现聚合属于同一簇的节点的池化操作。然而，Laplacian的特征分解代价很高，而且由于聚类结果是特定于图的，因此基于SC的池化方法必须对每个新样本执行新的优化。在本文中，我们提出了一种图聚类方法来解决SC的这些局限性。我们建立了归一化minCUT问题的连续松弛公式，并训练GNN来计算最小化这一目标的簇分配。我们的基于GNN的实现是可微的，不需要计算谱分解，并且学习了一个聚类函数，可以在样本外的图上快速评估。从提出的聚类方法出发，我们设计了一个图池化算子，它克服了现有图池化技术的一些重要局限性，并在多个监督和非监督任务中取得了最好的性能。

网址： https://arxiv.org/abs/1907.00481

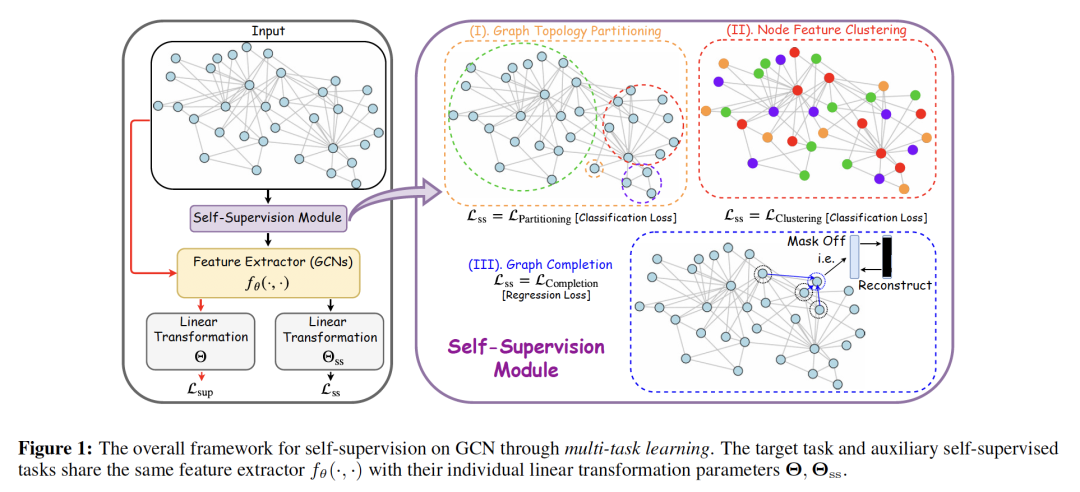
6. When Does Self-Supervision Help Graph Convolutional Networks?

作者：Yuning You, Tianlong Chen, Zhangyang Wang, Yang Shen

摘要：自监督作为一种新兴的技术已被用于训练卷积神经网络(CNNs)，以提高图像表示学习的可传递性、泛化能力和鲁棒性。然而，自监督对操作图形数据的图卷积网络(GCNS)的介绍却很少被探索。在这项研究中，我们首次将自监督纳入GCNS的系统探索和评估。我们首先阐述了将自监督纳入GCNS的三种机制，分析了预训练&精调和自训练的局限性，并进而将重点放在多任务学习上。此外，我们还提出了三种新的GCNS自监督学习任务，并进行了理论分析和数值比较。最后，我们进一步将多任务自监督融入到图对抗性训练中。研究结果表明，通过合理设计任务形式和合并机制，自监督有利于GCNS获得更强的泛化能力和鲁棒性。