深度学习模型陷阱：哈佛大学与OpenAI首次发现“双下降现象”

---

   新智元报道  

来源：openai

编辑：向学

【新智元导读】哈佛大学与OpenAI的研究者最新发现“双下降现象”：随着模型大小、数据大小或训练时间的增加，性能先提高，接着变差，然后再提高。这可能会导致“Bigger models may be worse, more samples maybe hurts”。虽然这种行为似乎相当普遍，但我们尚未完全了解其发生的原因，因此这是一个值得进一步研究的重要研究方向。你怎么看？现在戳右边链接上 新智元小程序 了解更多！

近日，哈佛大学Preetum Nakkiran等研究者与人工智能研究组织OpenAI的研究者Ilya Sutskever最新研究发现，包括卷积神经网络（Convolutional Neural Networks，CNNs）、残差网络（Residual Networks，ResNets）与Transformers的许多现代深度学习模型均会出现“双下降现象”（Double Descent Phenomenon）：随着模型大小、数据大小或训练时间的增加，性能先提高，接着变差，然后再提高。其峰值出现在一个“临界区”，即当模型几乎无法拟合训练集时。当增加神经网络中的参数数目时，测试误差最初会减小、增大，而当模型能够拟合训练集时测试误差会经历第二次下降。这种效果通常可以通过仔细的正则化来避免。虽然这种行为似乎相当普遍，但我们尚未完全了解其发生的原因， 因此这是一个值得进一步研究的重要研究方向。

论文地址：https://arxiv.org/pdf/1912.02292.pdf

这既不同于古典统计学家认为太大的模型更差的传统观点，也不同于现代机器学习认为更大模型会更好的范式；且“双下降现象”也发生于训练的epoch增加时。

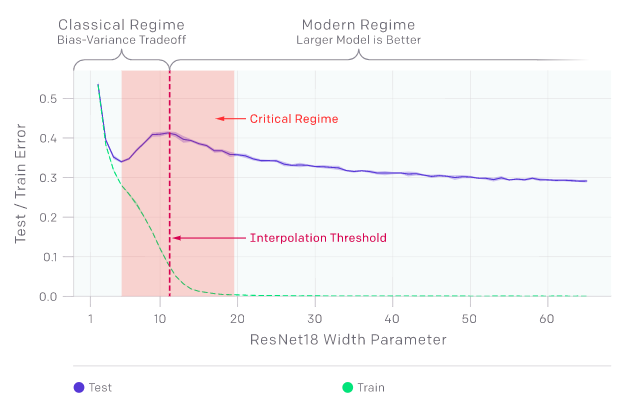
训练和测试误差是模型大小的函数

“双下降现象”可能会导致产生“training on more data hurts”的区域。上图中测试误差的峰值出现在插值阈值附近，而此时模型的大小刚好不足以拟合训练集。在该研究观察到的所有情况下，影响插值阈值的变化（如改变优化算法、训练样本数或标签噪声量）也相应地影响测试误差峰值的位置。“双下降现象”在添加标签噪声的设置中最为突出；如果没有标签噪声，那么峰值较小因此容易丢失；而添加标签噪声则会放大这种一般行为，并使我们能够轻松地进行调查。

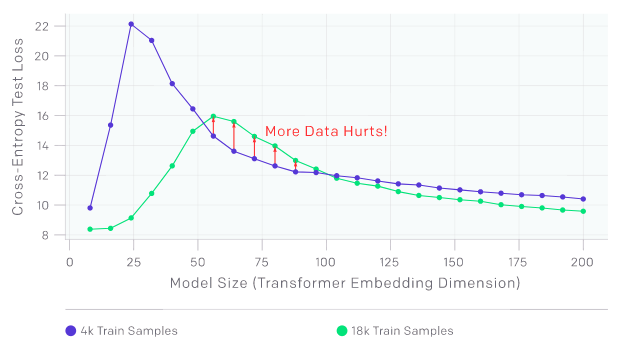
测试损失是Transformer模型大小的函数

“样本非单调性”可能会导致产生“more samples hurts”的区域。上图为在没有添加标签噪声时接受语言翻译任务训练的Transformer。正如预期的那样，在增加样本数时会使曲线向下移动，以降低测试误差；然而，由于更多样本需要更大模型来拟合，因此增加样本数也会使插值阈值（与测试误差的峰值）向右移动。对于中等大小的模型（红色箭头标识），这两种效果的结合使在4.5倍以上的样本上进行的训练实际上会降低测试性能。

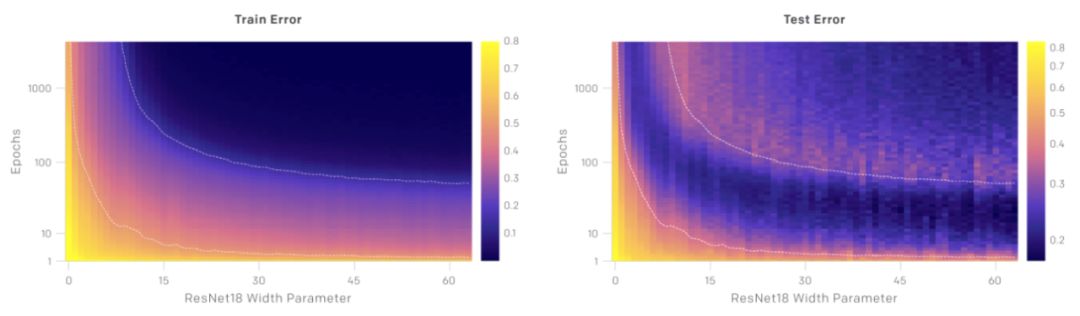
测试误差、训练误差是模型大小与训练epoch的函数

测试误差与训练误差既是模型大小的函数，也是训练epoch的函数。在上图中，对于给定数量的优化步骤（固定y坐标），测试误差和训练误差表现为模型大小的“双下降”；对于给定的模型大小（固定x坐标），随着训练的进行，测试误差和训练误差减小、增加、再次减小。一般来说，测试误差的峰值系统地出现在当模型几乎不能拟合训练集时。

参考资料：

https://openai.com/blog/deep-double-descent/

寒冬里，这个最酷AI创新平台招人啦！新智元邀你2020勇闯AI之巅

在新智元你可以获得：

• 与国内外一线大咖、行业翘楚面对面交流的机会

• 掌握深耕人工智能领域，成为行业专家

• 远高于同行业的底薪

• 五险一金＋月度奖金＋项目奖励＋年底双薪

• 舒适的办公环境（北京融科资讯中心B座）

• 一日三餐、水果零食

新智元邀你2020勇闯AI之巅，岗位信息详见海报：