你的模型刚不刚？谷歌提出“刚度”概念，探索神经网络泛化新视角

---

  新智元报道  

来源：arxiv

编辑：肖琴

【新智元导读】Google AI的研究人员的最新研究提出一个全新概念：刚度(Stiffness)，为探索神经网络的训练和泛化问题提供了一个新视角。

Google AI的研究人员最近在arxiv发表的一篇新论文，探索了神经网络的训练和泛化问题的一个新视角。

论文题为“Stiffness: A New Perspective on Generalization in Neural Networks”，作者是谷歌 AI 苏黎世研究中心的Stanislav Fort等人。

论文提出“刚度”(stiffness)这个概念，透过这个概念研究了神经网络的训练和泛化问题。

研究人员通过分析一个示例中的小梯度步骤如何影响另一个示例的损失来测量网络的“刚度”。

具体来说，他们在4个分类数据集(MNIST、FASHION MNIST、CIFAR-10、CIFAR-100)上分析了全连接卷积神经网络的刚度。他们关注的是刚度如何随着1) 类隶属度(class membership），2)数据点之间的距离，3)训练迭代，和4)学习率而变化。

研究表明，当在固定的验证集上计算时，刚度与泛化(generalization)直接相关。刚度函数的灵活性较差，因此不太容易对数据集的特定细节进行过拟合。

结果表明，“刚度”的概念有助于诊断和表征泛化。

学习率的选择对学习函数的刚度特性有显著影响。高学习率会导致函数逼近在更大的距离上“更刚”(stiffer)，并且学习到的特征可以更好地泛化到来自不同类的输入。另一方面，较低的学习率似乎能学到更详细、更具体的特征，即使在训练集上导致同样的损失，也不能泛化到其他类。

这表明，高学习率的优势不仅在于收敛所需的步骤更少，还在于它们倾向于学习的特性具有更高的泛化性，即高学习率充当了有效的正则化器。

刚度(Stiffness)的定义

刚度的定义如下：

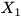
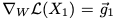
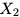
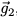
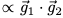
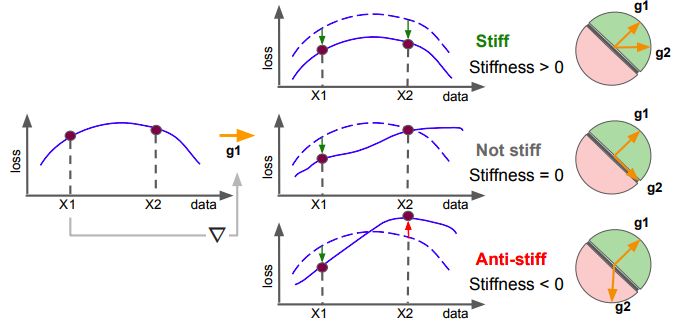
如果点处的损失相对于网络权重的梯度是，并且点处的梯度是 ，则我们定义“刚度”为。

图1：“刚度”概念的图示

如图1所示，“刚度”可以看做是通过应用基于另一个输入的梯度更新引起的输入损失的变化，相当于两个输入的梯度之间的梯度对齐(gradient alignment)。

实验和结果

基于类隶属度关系的刚度特性

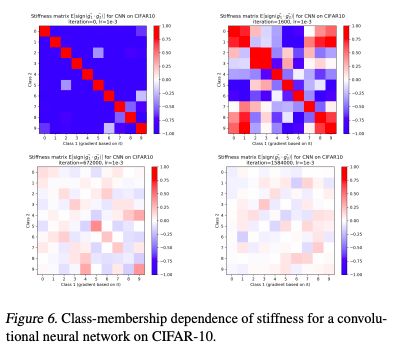
我们基于验证集数据点的类隶属度(class membership )作为训练迭代函数，研究了验证集数据点的刚度特性。

对于带有真实标签的MNIST、FASHION MNIST和CIFAR-10数据集，结果分别显示为图3、图5、图6，对于带有随机排列训练集标签的MNIST数据集，结果为图4.

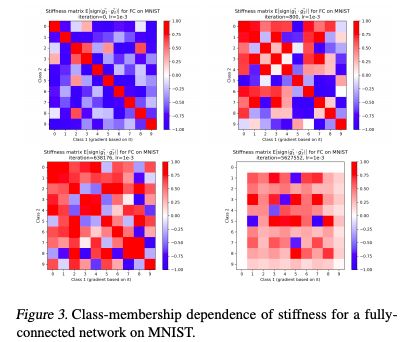
图3：MNIST上完全连接网络刚度的Class-membership dependence

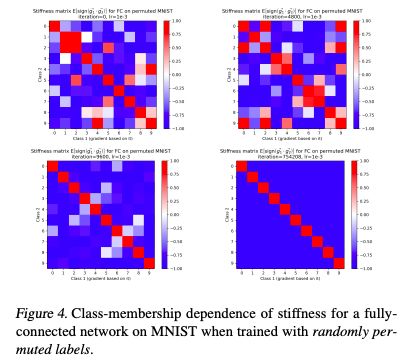
图4：MNIST上完全连接网络刚度的Class-membership dependence，训练时使用随机排列的标签。

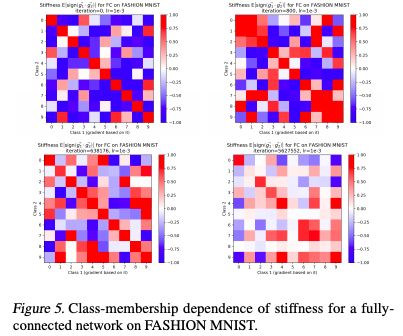
图5：FASHION MNIST上完全连接网络刚度的Class-membership dependence

图6：CIFAR-10上卷积神经网络刚度的Class-membership dependence

图3、图5和图6都显示了4个训练阶段的刚度矩阵：初始化阶段(任何梯度步骤之前)、优化早期阶段和两个后期阶段。

学习率对刚度的影响

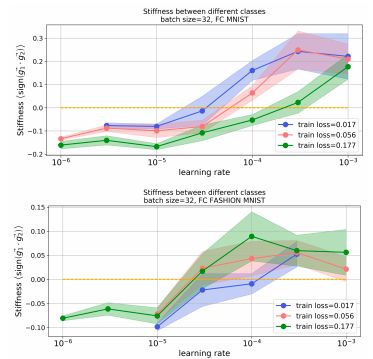
图8：在MNIST 和 FASHION MNIST上以不同学习率训练，不同类别的刚度。

如图8所示，这两幅图给出了三种不同训练损失的 class dependent刚度矩阵。较高的学习率导致来自不同类的输入之间的刚度更高，表明它们学习的特性在不同类之间更加可泛化(generalizable)。

结论

我们探讨了神经网络刚度的概念，并用它来诊断和表征泛化。我们研究了在真实数据集上训练的模型的刚度，并测量了其随训练迭代、类隶属度、数据点之间的距离和学习率的选择而变化的情况。为了探讨泛化和过拟合，我们重点研究了验证集中数据点的刚度。

总结而言，本文定义了刚度的概念，证明了它的实用性，为更好地理解神经网络中的泛化特性提供了一个新的视角，并观察了其随学习率的变化。

论文地址：

https://arxiv.org/pdf/1901.09491.pdf

---

新智元春季招聘开启，一起弄潮AI之巅！

岗位详情请戳：

【春招英雄贴】新智元呼召智士主笔，2019勇闯AI之巅！

【2019新智元 AI 技术峰会倒计时7天】

 2019年的3月27日，新智元再汇AI之力，在北京泰富酒店举办AI开年盛典——2019新智元AI技术峰会。峰会以“智能云•芯世界“为主题，聚焦智能云和AI芯片的发展，重塑未来AI世界格局。

同时，新智元将在峰会现场权威发布若干AI白皮书，聚焦产业链的创新活跃，评述华人AI学者的影响力，助力中国在世界级的AI竞争中实现超越。

购票二维码

活动行购票链接：http://hdxu.cn/9Lb5U

点击文末“阅读原文”，马上参会