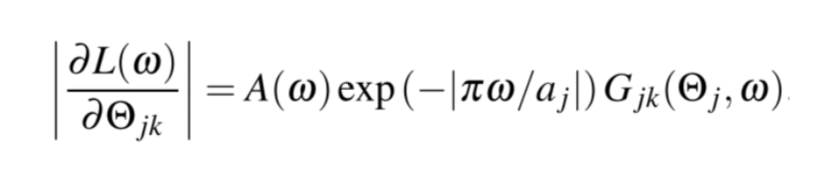从傅里叶分析角度解读深度学习的泛化能力

2018 年 8 月 24 日 PaperWeekly

作者丨许志钦

学校丨纽约大学阿布扎比分校博士后，纽约大学库朗研究所访问学者

研究方向丨计算神经科学，深度学习理论

深度学习成功地应用在很多领域，但对它的理论理解却非常缺乏。这两年，很多理论学家把关注点放在一个关于深度学习与传统学习理论的悖论上。在传统学习理论中，模型的参数越多，模型一般会更好地拟合训练数据，但模型的泛化能力（拟合测试数据集的能力）会变差。在深度学习中，参数的数目比训练数据集要大得多，但深度网络（DNN）却通常既能拟合好训练数据，又保持良好的泛化能力。这个违反直觉的现象被大家称为“明显悖论” (apparent paradox)。

频率原则（F-Principle）

最近有几篇文章 [1,2,3] 从傅里叶分析的角度，在实验和理论上揭示了该悖论背后的一种机制。

▲ 文献1

▲ 文献2

▲ 文献3

一般来说，在深度学习中，大家用来测试结论的例子或者是手写数字集（MNIST），或者是图像分类集（CIFAR）。这两类数据集相对实际应用的数据集确实已经足够简单，但在分析上，它们仍是非常复杂的，因为它们的输入维度仍然非常高（像素点的个数）。

我们可以从拟合一维函数出发考虑这个问题。训练数据集是少数几个均匀采样数据点，如果用多项式去拟合，阶数很高的时候（大于数据点个数），拟合的结果通常是一个能够精确刻画训练数据但振荡厉害的函数。但如果用 DNN，无论多大规模，通常学习到的曲线都是相对平坦的。因为是一维函数，所以很容易想到，振荡和平坦可用傅里叶分析定量地刻画。于是就自然能猜想到，DNN 在学习的时候可能更加偏爱低频成分。

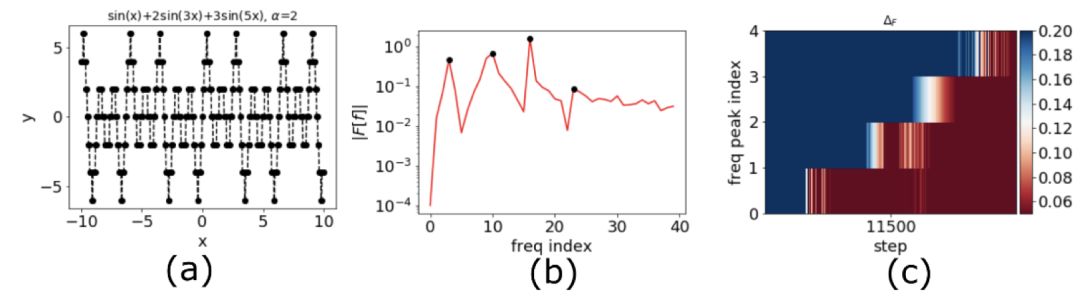
下面是一个一维函数的例子 [1]（图 1a 中的黑点），对数据作离散傅里叶变换后如图 1b 所示，考虑图 1b 中的频率峰值（黑点）在训练中的相对误差，如图 1c，频率越高，收敛越慢（蓝色表示相对误差大，红色表示相对误差小）。频率原则可以粗糙地表述成：DNN 在拟合目标函数的过程中，有从低频到高频的先后顺序。（Frequency Principle or F-Principle in [1], or spectral bias in [2]）

▲ 图1

F-Principle 并不是一个陌生的概念，而是我们日常生活中经常都在用的一个原则。想象一下，如果让一个人去记住一个没见过的东西，一般比较粗糙的轮廓信息会先被记住，然后再是很多细节。没错，DNN 也正是使用了这样的一个学习过程。举一个例子，我们来训练一个 DNN 来记住一张图片。DNN 的输入是一个位置坐标 (x,y)，我们希望它输出这个位置对应的灰度值。图 2 的一系列图展示了不同训练步数，DNN 学习到的图像，正如我们前面所猜测的从粗糙的轮廓到细节的学习过程。

▲ 图2

经验上理解深度学习的泛化能力

一般来说，“平坦”简单的函数会比振荡复杂的函数有更好的泛化能力。DNN 从目标函数的低频成分开始学习。当它学到训练数据的最高频率的时候，此时频率空间误差趋近于零。因为频率空间的误差等于实域空间的误差，所以它的学习也基本停止了。这样深度学习学到的函数的最高频率能够被训练数据给限制住。对于小的初始化，激活函数的光滑性很高，高频成分衰减很快，从而使学习到的函数有更好的泛化能力。

对于低频占优的目标函数，小幅度的高频成分很容易受到噪音的影响。基于频率原则，提前停止训练（early-stopping）就能在实践中提高 DNN 的泛化能力。

理论上理解深度学习的泛化能力

从低频到高频的学习原则并不总是对的，比如在文献 [1] 中讨论到的，如果目标函数是随机数据点（频率空间没有低频占优的特性），或者 DNN 的参数的初始化的值比较大，这个原则就会失效。特别是在大初始化的情况下，DNN 的泛化能力也会变差。

文献 [2] 对 DNN 学习到的函数的频率幅度的估计并不能解释这些现象。特别地，对于层数和神经元数目足够多的 DNN，文献 [2] 给出的理论不能解释为什么 DNN 从低频开始学习。在文献 [2] 中，DNN 的拟合函数的高频成分受权重（weights）的谱范数（spectral norm）控制。对于小规模的DNN，可以经常观察到，权重的范数随训练而增长，从而允许小规模的 DNN 去拟合目标函数中的高频成分。因此，文献 [2] 在理论上给出频率原则的一种可能解释。

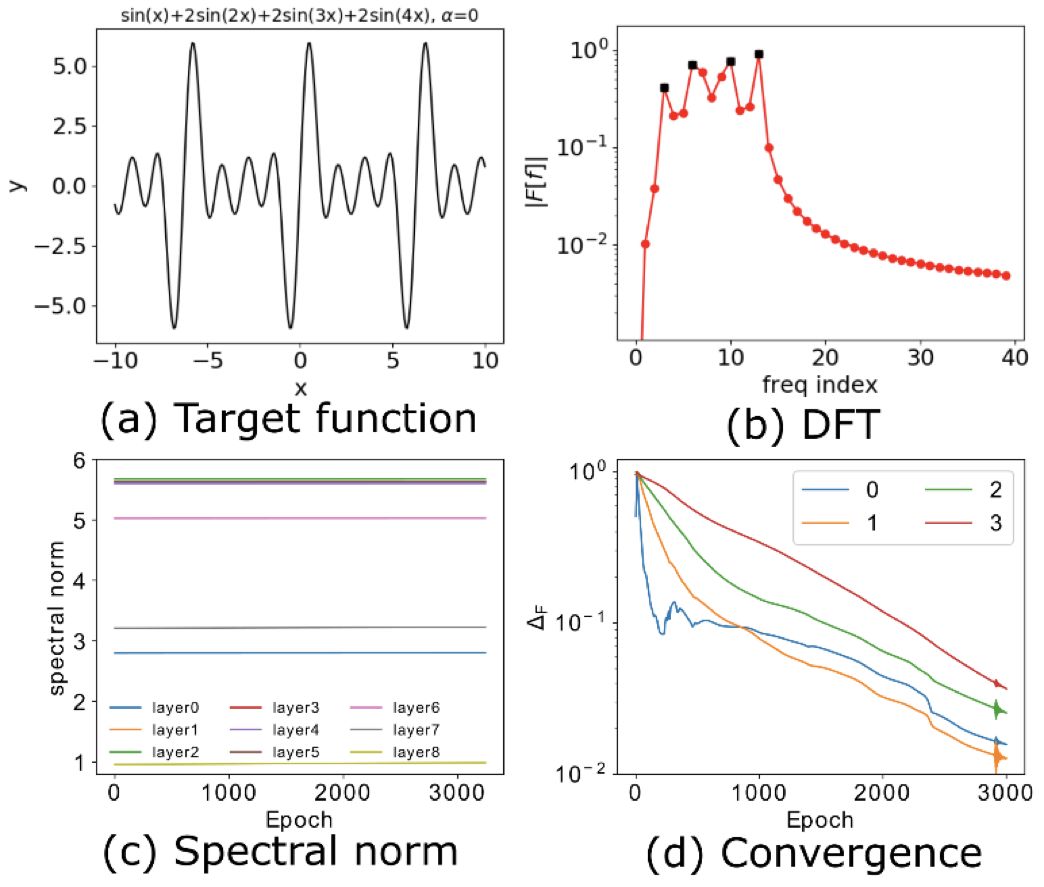
但如文献 [3] 的一个例子所示（下图，图 3a 为目标函数，图 3b 为其离散傅里叶变换），对于层数和神经元数目足够多的 DNN，权重的谱范数（图 3c）基本不变。但如图 3d 所示的频率成分的相对误差，四个重要的频率峰值（图 3b 的黑点）仍然是从低频开始收敛。对于这种情况，文献 [2] 对 DNN 的拟合函数的高频成分的上限估计在训练过程中基本不变，从而不能看出低频到高频学习的频率原则。

▲ 图3. 说明：(d) 展示 (b) 中四个频率峰值在训练中的相对误差

文献 [3] 给出了能够解释这些问题的理论框架。从只有一层隐藏层的 DNN（sigmoid 作为激活函数）开始，在傅里叶空间分析梯度下降算法，文献 [3] 得到损失函数 ω 在任一频率分量上对任一参数的导数。

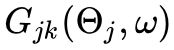
其中，是对应神经元的权重（weight），是关于对应神经元所有参数和频率 ω 的一个多项式，A(ω) 是学习到的函数与目标函数的差的幅度。文献 [3] 论述了这个表达式如何定性的推广到一般 DNN。

上面这个式子显示地定量地说明了在梯度下降过程中低频成分会有更高的优先级。但同时需要注意的是，这个优先级不只是由频率决定，它也依赖于拟合函数与目标函数的差的幅度。

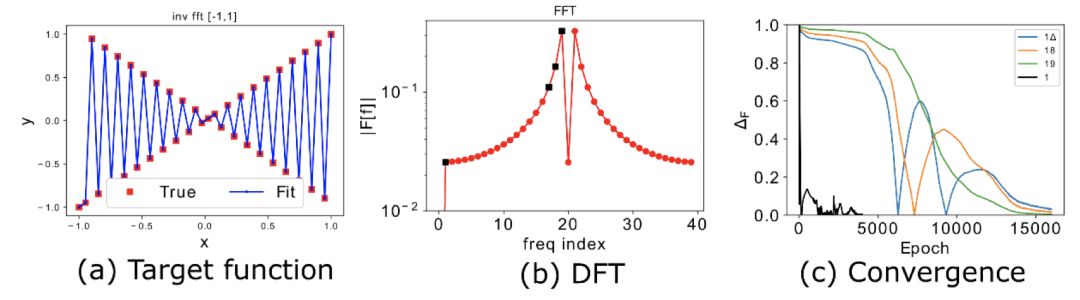
这个理论分析揭示了对于低频占优的目标函数，当 DNN 的参数是很小的数时，低频成分会先收敛，并且在低频成分收敛的时候，DNN 的高频成分仍然很小。而当 DNN 拟合高频成分的时候，已经收敛的低频成分只会受到很小的干扰。对高频占优的函数，整个训练过程就会变得复杂。低频容易受到高频的影响，所以低频是振荡式的收敛，每振荡一次，偏离的最大幅度就会下降。并且频率越低，振荡越频繁（如下图 4 所示）。

▲ 图4

对于初始化的问题，这个理论框架也给出了解释。如果初始化权重很大，由于上式中的很大，低频不再占优，所以频率原则就很容易失效。并且，激活函数的高频成分也会变大。对于那些频率高到训练数据也看不到的成分，因为训练过程不能限制它们，所以在训练完成后，它们仍然有比较大的幅度而导致 DNN 的泛化能力变差。

总结

傅里叶分析的理论框架非常好地解释了 DNN 为什么在拥有大量参数的情况下既能学好训练数据，又能保持好的泛化能力，简单地说，由于频率原则，DNN 学习到的函数的频率范围是根据训练数据的需要而达到。对于那些比训练数据的最高频率还高的频率成分，DNN 能保持它们幅度很小。

用傅里叶分析的角度来研究 DNN 的学习问题仍处于开始的阶段，有很多有趣的问题值得继续深入，比如更加定量地分析 DNN 的学习过程，理解层数和每层宽度对训练的不同贡献等等。

致谢：感谢张耀宇对本文初稿的校正和修改。

参考文献

[1]. Zhi-Qin J. Xu, Yaoyu Zhang, Yanyang Xiao. Training behavior of deep neural network in frequency domain, arXiv preprint arXiv: 1807.01251. (May 18, 2018 submitted to NIPS, first submitted to arXiv on Jul 3, 2018)

[2]. Nasim Rahaman, Devansh Arpit, Aristide Baratin, Felix Draxler, Min Lin, Fred A. Hamprecht, Yoshua Bengio, Aaron Courville. On the spectral bias of deep neural networks, arXiv preprint arXiv:1806.08734. (First submitted to arXiv Jun 22, 2018)

[3]. Zhi-Qin J. Xu. Understanding training and generalization in deep learning by Fourier analysis, arXiv preprint arXiv: 1808.04295. (First submitted to arXiv on Aug 14, 2018)