【泰勒级数】- 微积分的本质 10

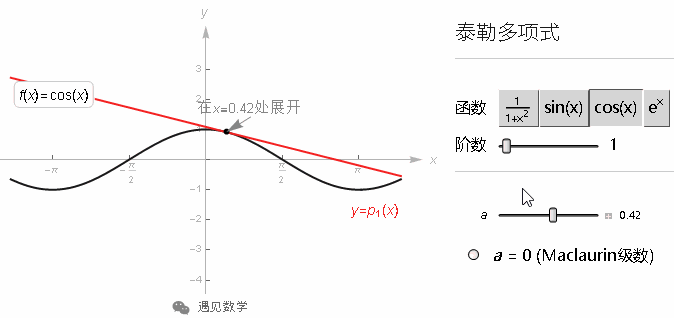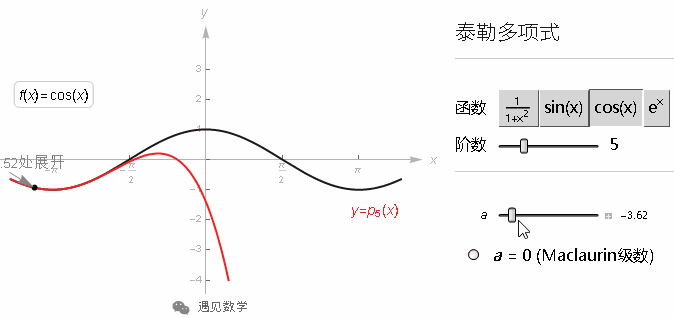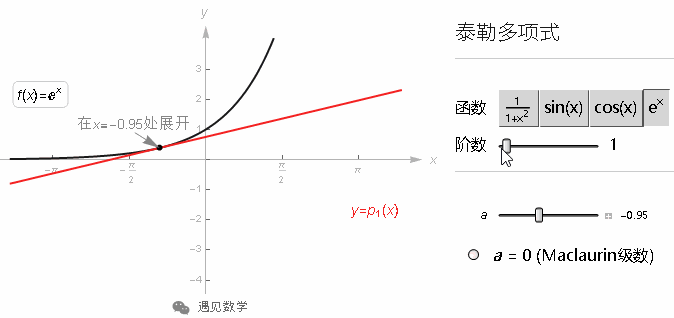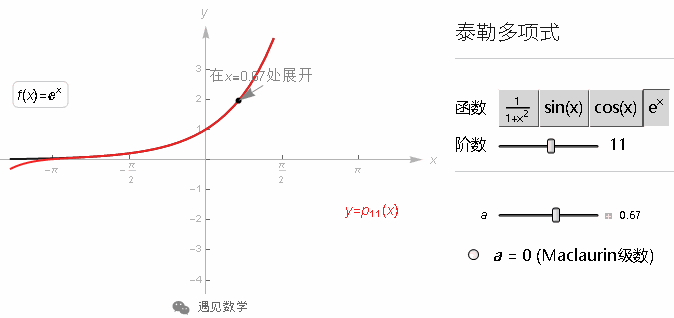
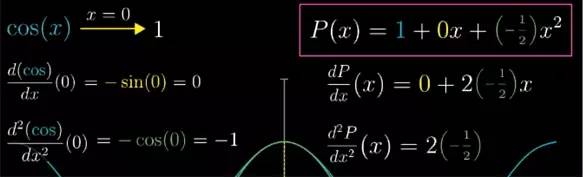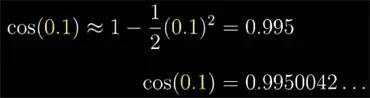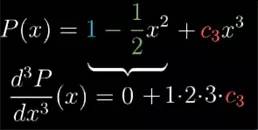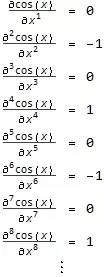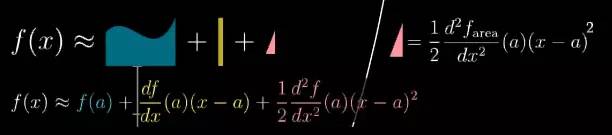来自3Blue1Brown《微积分的本质》视频:https://space.bilibili.com/88461692

(点击最下阅读原文查看B站更多精彩内容) 这里特别感谢各位翻译的贡献:昨梦电羊，罗兹，Solara570，圆桌字幕组等。 有意的译者请移步B站进行联系！

[遇见数学]根据视频内容整理文字版, 方便各位同学学习, 先来看下视频吧.

正文

泰勒级数会经常的在数学物理类的工科学习中与我们相遇, 因为它在数学中是一种极其强大的函数近似工具.

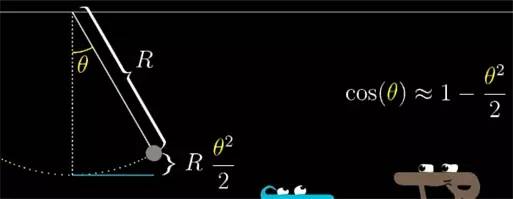
比如在单摆中实验中求摆离最低点高度表达式的时候, 这个距离会和 (1-cos(摆臂与垂直方向的夹角$\theta$)) 成正比, 这里的 cos 函数很难让我们看出单摆和其他振荡现象直接的关系. 但是如果你用 $1-\frac{{\theta }^2}{2}$ 去近似 cosθ), 问题就简单多了, 因为这只是你熟悉的二次多项式而已.

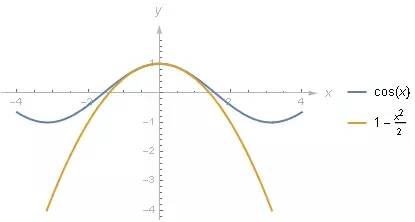
如果你把 $1-\frac{{\theta }^2}{2}$ 的图像和 cosθ) 绘制在一起的话, 起码在 0 附近两者确实非常接近.

但是你要怎样才能找到这个近似呢？ 这个二次表达式又是怎样得来的? 我们学习泰勒级数, 很大程度上就是为了在某个点附近用多项式函数去近似其他函数. 原因在于多项式要比很多函数要容易处理, 比较好计算, 容易求导, 而且好积分.

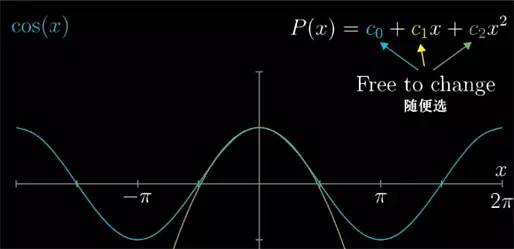
那么现在我们就以 cosθ) 为例看看, 花点时间考虑下, 在 x=0 处应该如何找到一个二次多项式来近似它. 也就是在所有可能的 $c_2{x}^2+c_{1}x+c_0$ 中, 要让这个多项式在 x=0 处最接近 cos(x) , 最合适的 $c_0$, $c_1$, $c_2$ 系数到底应该是多少, 所对应的多项式图像能和 cos 重合度最高.

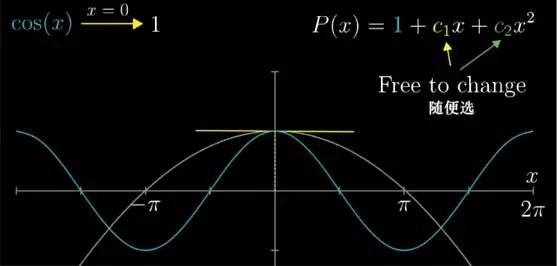
首先呢，在 x=0 处, 函数 cos(x)=1, 那我不管近似多项式的系数该取多少, 多项式在 0 处最好等于1. 代入 0 带入到 $c_2{x}^2+c_{1}x+c_0$ , 结果就是 $c_0$ 等于 1.

$c_0$ 定下来之后，不管我们让 $c_1$ 和 $c_2$ 等于多少，不管如何近似. 当 x=0 时, 多项式也都会一直等 1.

在 x=0 时, 如果我们让函数的切线斜率, 也能和 cos(x) 相等的话，那就更好了. 嗯，不然近似函数的值在离 x=0 处很近的地方就会有明显偏差了.

cos(x) 的导函数是 -sin(x) , 在 x=0 处为 0, 表示此时它的切线是水平的, 而我们近似函数的导数是 $c_1$ + 2*$c_2$*x , 再带入 x=0 就可以得到 $c_1$ . 也就是常数 $c_1$ 控制着在 x=0 处对导数的近似程度. 让 $c_1$=0, 我们的近似函数的导数也就变成了 0.

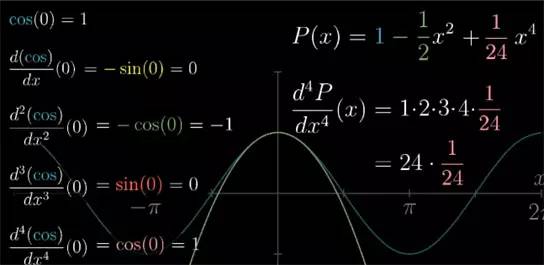
现在只剩下 $c_2$ 了, 由于它在 x=0 处的函数值和斜率都已经确定了, 那么就利用曲线的凹凸性吧. cos 函数的图像在 x=0 时向下弯曲(凹函数), 说明此时二阶导数为负.

换句话说，虽然此时 cos 函数的变化率等于 0, 但这个变化率的本身却在不断减小. 那么已知导函数是 -sin(x) , 二阶导函数是 -cos(x). 在 x=0 时, 它的二阶导数就等于 -1.

那么让二阶导数也相等, 就相当于又保证了在 x=0 处两者的弯曲程度也相同. 把近似多项式斜率的变化和 cos(x) 斜率的变化保持相近的程度.

对于之前多项式的导数，我们再次求导, 就可以得到多项式的二阶导数 2 $c_2$ . 要让 x=0 处二阶导数为 -1, 那么 2 $c_2$ 就必须等于 -1, 因此 $c_2$ = $-\frac{1}{2}$. 最终我们得到了近似函数.

为了试一试这近似程度到底好不好, 不妨先用它求一下 cos(0.1) 的近似值作对比:

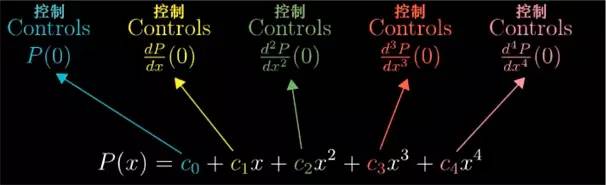
我们来回顾一下刚才的内容, 在这个二次函数中, 有三个系数来控制近似的程度, 3 个常量: $c_0$ , $c_1$ 和 $c_2$ .

$c_0$ 负责让多项式在 x=0 的值和 cos(0) 相一致;$c_1$ 负责让两者的导数相一致;$c_2$ 负责让两者的二阶导数相一致;

这样一来，利用这三个给定的系数, 当 x 的取值在 0 附近增减时, 近似函数值的变化率和近似函数值变化率的变化率就可以尽可能的接近函数 cos(x) 自身. 这个多项式近似，可以往上加几个更高层次幂的项来近似更高阶的导数, 比方说再加一个 $c_3$ $x^3$ , 多一个系数 $c_3$ . 对它取三阶导数, 那么二次项以及以下的部分就全部没有了.

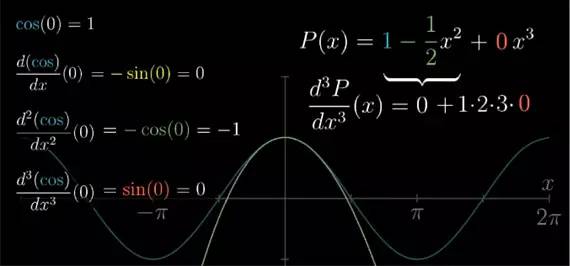
最后就只会剩下原来的三次项，它变成了 $\text{1*2*3}{c}_3$. 而另一边 cos(x) 的三阶导函数是 sin(x) 在 x=0 时等于 0. 怎么要上三阶导数一致的话, 此时常数 $c_3$ 就应该等于 0.

换句话说, $1-\frac{x^2}{2}$ 不仅仅是 cos(x) 在 x=0 处最佳的二次近似函数, 同时也是最佳的三次近似函数.

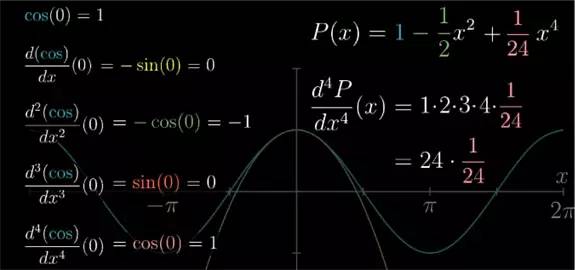
想要更好近似的话，再加个第四次项 $\frac{1}{24}$ $x^4$, 可以得到 $c_4=\frac{1}{24}$.

确实画出多项式函数 $\frac{x^4}{24}-\frac{x^2}{2}+1$ , 可以看到在 x=0 附近是非常接近 cos(x) 的.

从怎么解决物理问题牵扯到求一个很小的角度 cos 值的时候, 换成用这个多项式求出来的结果来近似, 其实就和真实的值基本上差不太多了.

现在我们来仔细回顾之前的过程, 首先，阶乘的形式是自然而然出现的, 你对 $x^n$ 连续取 n 次求导.

多项式求导法则一层套一层. 最后会剩下一个 1*2*3*...=n! 的常数. 所以近似多项式中第 n 项的系数并不是高阶导数本身.

例如, cos(x) 的四阶导数是 1, 那么 $x^4$ 的系数就是 $\frac{1}{4!}=\frac{1}{24}$

其实，当我们往近似多项式中添加更高次项时, 低阶的项并不会因此而改变，这就很重要.

例子中近似多项式的二次导数，不管后面更高次项长的什么样, 在 x=0 处的结果永远都是 2 乘以二次项系数.

对于其他阶的导数依然同理, 所以多项式任意 n 阶的导数在 x=0 时的值, 都由唯一的一个系数来控制.

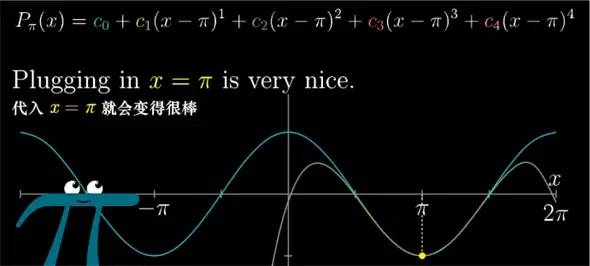
如果你想用多项式估计一个非零点附近的结果，就说 x=[Pi] 吧. 那么你换成使用关于 (x-[Pi]) 而不是 x 的多项式就可以得到相同的效果. 这对于任何点都是通用的.

虽然这样做使得式子看起来比较复杂，但我们做的无非和在 0 点处一样. 这样一来代入 x=[Pi] 就可以消掉某一项外的所有部分.

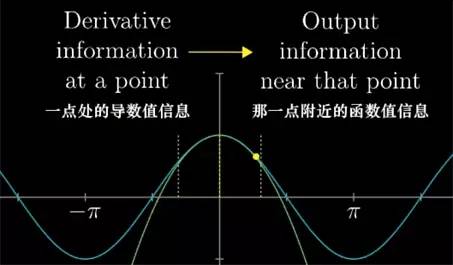
从另外的角度来看，在某一点时, 函数高阶导数值的信息, 多转换成在那一点附近函数值的信息.

对 cos(x) 而言, 我们取多少阶导数都无所谓, 它只会按照 cos(x), -sin(x), -cos(x), sin(x) 的形式一直循环下去, 那么在 x=0 , 它的各阶导数值也会按 1, 0, -1, 0 的形式循环

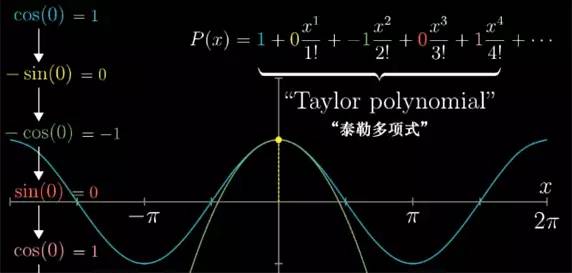
知道了 cos(x) 所有的高阶导数, 其实也就了解了关于 cos(x) 的许多信息, 即便只关注一个取值 x=0. 所以当知道了所有高阶导数, 我们就可以写出这么一个近似多项式. 让它在 x=0 时 的 n 阶 导数值也呈现 1, 0, -1, 0 这样相同的循环, 从而正好吻合 cos(x) 的性质.

要求出这个多项式，我们就让它每项的系数遵循同样的规律. 这样得到的多项式就叫做 cos(x) 的泰勒多项式.

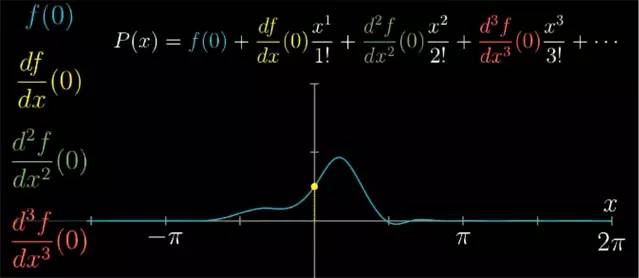
假设我们要近似的函数并不是 cos 函数, 你可以照样对它取 1阶, 2阶, 3阶, 甚至任意高阶的倒数, 算出它们在 x=0 处的值, 然后再构造近似多项式时, $x^n$ 项对应的系数就应该为 x=0 时函数的 n 阶导数值, 再除以 n!

现在你再看到这个多项式就请这么考虑:

更一般的来说, 如果你想近似 0 点之外, 比如 a 点附近的值的话, 就要用 (x-a) 来改写原多项式, 这样泰勒多项式就能适用于所有的情况了.

改变 a 的值就可以调节多项式函数在那个地方来近似原始函数, 并使多项式的高阶导数和函数的高阶导数在那一点相等

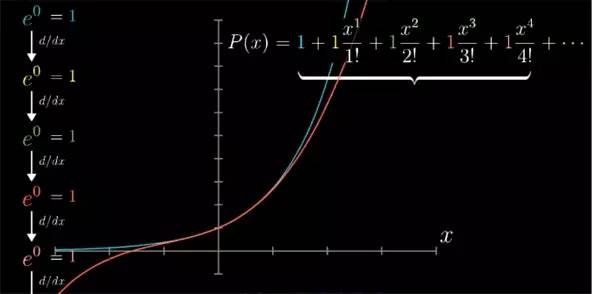
最简单有意义的例子莫过于 x=0 附近时的 $e^x$ 函数了. 高阶导数非常好算，因为它的导数就是它本身. 在 x=0 点, 它们全是 1, 这就表示近似多项式应该写成下面形式:

这便是 $e^x$ 的泰勒多项式.

现在把它和之前学的微积分内容串联起来, 用几何来解释泰勒多项式的二次项.

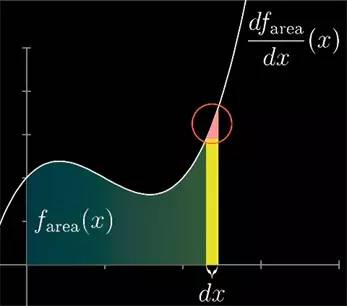
我们会用到微积分基本定理, 考虑一个函数图像之下的面积, 左边的下限点是固定的，右边的上限点是可变的, 现在考虑如何近似这个面积函数, 而不是近似这个函数本身.

利用面积去思考问题的话, 多项式的二次项很容易用图形来解释. 回想一下微积分基本定理，说的是图像所表示的函数本身就是面积函数的导数, 这是因为如果函数往右增加一小段 dx, 多出来的这点面积就可以近似为 dx*函数此时的高度. 而这个近似会随着 dx 越来越少而变得越来越精确.

但如果 dx 不逼近 0 时, 面积的变化想近似的更准确的话, 你就得考虑这部分的面积，它可以近似为一个三角形:

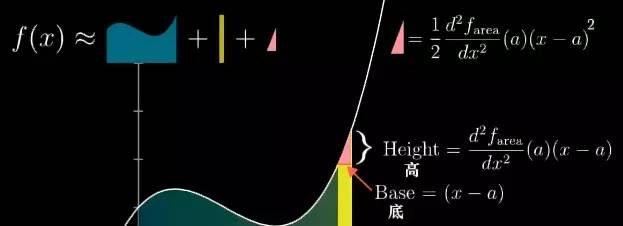
现在我们以 a 为取值起点, 设变换后取值为 x, 那么取值的变化量就是 (x-a), 这个变化量也是这个三角形的底, 而三角形的高就是图像的斜率乘以 (x-a) .

由于曲线图像代表了面积函数的导数, 所以在 a 点的图像斜率就是面积函数在 a 点的二阶导数.

因此, 这个三角形的面积, $\frac{1}{2}$ base*height 就是下面所示:

这种和泰勒多项式的二次项一模一样了.

假设已知面积函数 f 在 a 附近的导数信息要近似在 x 时的面积, 你就可以在先求 a 时的面积 f(x), 然后加上这个矩形的面积 (一阶导数)*(x-a), 然后再加上这三角形的面积.

上面是中的每一项都有明确的意义，并且都能在图中找到对应的部分.

或许你会考虑泰勒公式这个强大的工具能不能推广到无限项, 也就是累加无限多个项是不是还成立？数学上，我们把无限多项的和叫做级数(Series). 之前我们来近似函数, 累加有限多项的式子叫做泰勒多项式. 而累加无限多项就该叫做泰勒级数.

累加无限多的项其实并没有太大意义, 但是作为某个级数, 它展开的项越多, 它的和就越接近某个确定的数值的话, 我们就可以说这个级数是收敛(converge)的那个值.

举个例子, $e^x$ 的泰勒级数带入 x=1, 在加上越来越多项后, 总和就越来越接近 e, 那么可以说这个无穷级数收敛到 e, 或者说这个级数就等于 e.

事实上不管你代入什么 x , 例如 x=2, 然后再去计算越来越多项的泰勒多项式的话, 最终结果都会收敛的 $e^x$, 例如 x=2 就收敛到 $e^2$.

不管 x 离 0 有多远，这个性质对所有 x 都成立, 即便从定义上讲，泰勒级数只考虑 0 点周围的各种导数性质.

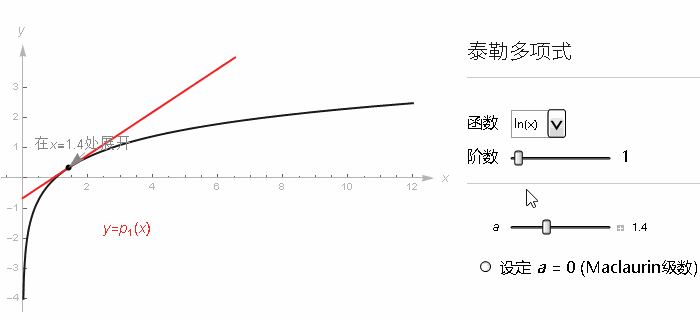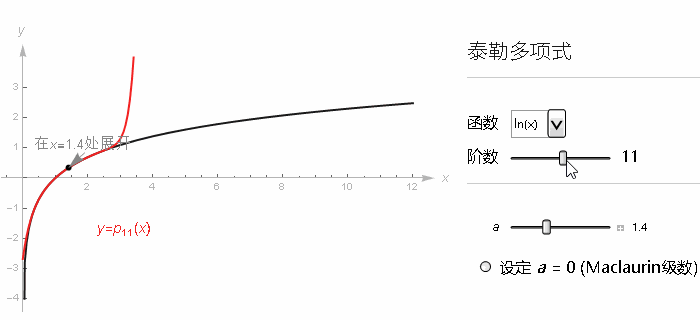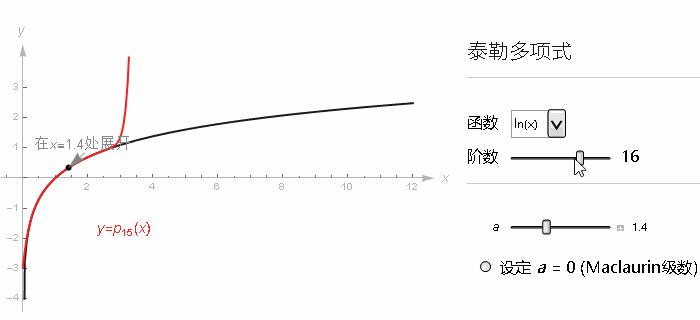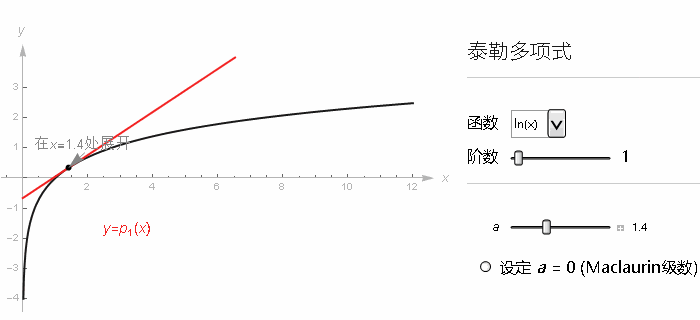
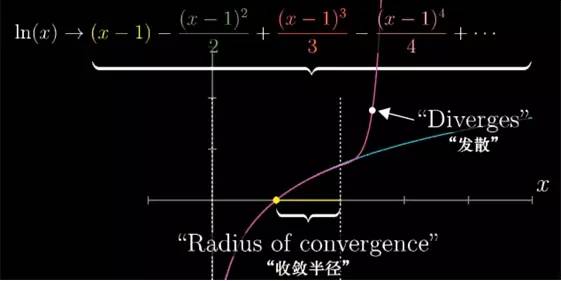
尽管 sin, cos 之类的一些重要函数依旧等价其泰勒级数, 但有的函数, 用某一取值所构建的级数只能在附近的范围中收敛, 就比如 ln(x) 在 x=1 附近, 用泰勒级数来近似 ln(x). 我们用相同的手法, 看 x=1 它的各阶导数. 级数最后就长这样.

当 x 的取值在 0 到 2 之间的话, 随着级数项越来越多, 我们就越来越接近自然对数的真实结果.

但是出了这个取值范围, 这个级数就不再接近任何值了, 再往上加更多项的话, 整个的和就会反复乱跳, 并且也不会逼近自然对数的真实取值了. 但我们知道 ln(x) 里 x 取 2 以上是完全没有问题的.

某种意义上讲, 我们在 x=1 取得的导数信息并不能拓展到更广的取值范围, 像这种, 累加更多的项的和并不能逼近一个值的级数, 我们就说它是发散(Diverges)的.

此外, 我们把在用来近似原始函数的那个点周围能够让多项式的和收敛的最大取值范围称作这个泰勒级数的收敛半径(radius of convergence).

关于泰勒级数还有很多可以学习的地方, 比如级数应用的案例, 如何找出近似的最大误差, 判断级数收不收敛的测试等等.

当然, 关于微积分就有更多东西可以学了, 但本系列最重要的目的就是帮你建立基础直觉, 给你信心, 给你自己继续学习的动力, 而泰勒级数中, 我希望大家建立并牢记的重要直觉就是: 泰勒级数是利用函数某个点处的导数, 来近似这个点附近函数的值.

最后感谢 3Blue1Brown 推出这么精彩有趣的视频, 也衷心地感谢字幕组的那些朋友，真的非常谢谢! 稍等几天[遇见数学]会出一个合辑来更方便大家学习, 希望各位继续关注和支持!

「予人玫瑰, 手留余香」

如果感到本文有些许帮助, 感谢转发, 支持本号更快发展! 

遇见数学

拨开知识的层层密林，探寻美妙数学中的趣味。

感谢关注遇见数学!