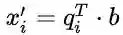博客 | MIT—线性代数（下）

2018 年 12 月 20 日 AI研习社

本文原载于知乎专栏“AI的怎怎，歪歪不喜欢”，AI研习社经授权转载发布。欢迎关注 邹佳敏 的知乎专栏及 AI研习社博客专栏（文末可识别社区名片直达）。

社长提醒：本文的相关链接请点击文末【阅读原文】进行查看

1、投影矩阵与最小二乘：向量子空间投影在机器学习中的应用最为广泛。就拿最小二乘的线性拟合来说，首先根据抽样特征维度假设线性方程形式，即假设函数。

线性代数的角度：将样本数据代入假设函数中，构建线性方程组Ax=b。若样本个数明显多于特征维度，则b很有可能没有落在A的列空间中，因此方程组无解。此时，可以取 A^T·A·x’=A^T·b ，将 b 投影到A的列空间中，求解投影向量所对应的x’。所以，一旦采用 A 转置的处理，求解的系数x’仅仅是原方程Ax=b的最佳估计，此时将投影过程中产生的法向量e认为是误差，被从原始b中减去，得到投影向量p。但需要格外注意的是，采用这种方法的前提是A的列向量必须满秩，保证 (A^T·A) 可逆。所以，在机器学习中，通常会预处理样本数据，保证输入到假设函数中的特征维度线性无关！

统计学角度：在线性回归中通常认为误差项仅仅出现在y的维度上，而特征维度x间不存在任何误差，所以，将样本数据代入假设函数，只站在y的角度定义损失函数

，然后对x分别取偏导数=0，最小化 e^2 ，最后发现取完偏导数=0后的方程组与前文中投影后的方程组相同，数学真的是很神奇！

求得 x’=(A^T·A)^{-1}·A^T·b 。

2、正交矩阵与Gram-Schmidt正交化：前文提到过正交向量， a^T·b=0 ；正交空间，行空间与零空间互为Rn空间正交补，两者交于零向量。这里要学习一个新名词，正交基和正交矩阵，在说明正交基时，通常定义标准正交基，即正交基之间内积为0，本身模长为1。如果方阵Q的所有列均是标准正交的，就被称作正交矩阵，即通常意义正交矩阵要满足方阵和列向量标准正交两个条件。因此可以得到， Q^T·Q=I，Q^T=Q^{-1} ，则若将向量b投影到列空间正交的矩阵中，投影矩阵为 P=Q·Q^T ，特别的，若投影到正交空间，则投影矩阵就是单位阵I。因为正交矩阵本身可以撑满整个Rm空间，投影就是其本身。所以，正交矩阵在机器学习中也有非常多的应用，通常会将样本空间A标准正交化为Q，就有投影后的 x’=Q^T·b ,则

。这里，标准正交化的方法就是Gram-Schmidt方法，该方法的核心就是投影，特别的，这里选取的是除去了投影向量p后产生的法向量e，同时对e单位化。

3、行列式及其性质：

矩阵行列式的值中包含了矩阵尽可能多的信息。有关行列式的计算，有3点基本性质和7点衍生性质，一切有关行列式的计算都包含在上述10条简单的性质里。①单位矩阵行列式=1；②交换矩阵两行，行列式符号改变；③如果我用t乘以矩阵一行，而其他行保持不变，行列式扩大t倍，或矩阵行列式可以依某一行线性可加；④若矩阵两行相同，行列式为0。可以使用②证明；⑤若第I行减去第K行，行列式不变。可以使用③+④证明；⑥矩阵中存在零行，行列式为0。可以使用③证明；⑦将矩阵消元化简为三角阵，行列式为对角线乘积。可以使用⑤证明；⑧当且仅当矩阵奇异时，行列式为0。可以使用⑦证明；⑨|A·B|=|A|*|B|；(10)矩阵转置，行列式不变。可以使用A=L·U+⑦+⑨证明。以上性质对列同样有效。

4、行列式公式与代数余子式：教授从二维矩阵及其性质③出发，严格推导出行列式公式的一般通项，即每行每列都具有唯一元素的所有矩阵行列式加总，行列式个数为n!项。再使用置换将所有矩阵转换为对角线型，同时伴随着符号的变换，这也是逆序数变换符号的来历。而使用代数余子式计算行列式的方法，也可以利用通项公式按某一行元素重新结合直接得到，同时，代数余子式的符号也由对应元素的下标和决定。以上公式对列同样有效。

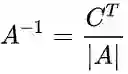
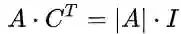
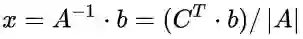
5、逆矩阵、克拉默法则和体积：由二维矩阵的逆矩阵公式可以看出，逆矩阵可以由矩阵行列式和代数余子式得到，具体的，逆矩阵=伴随矩阵/行列式，伴随矩阵为相对应元素代数余子式矩阵的转置，即。另一方面，该表达式的正确性可通过求证得到。有了逆矩阵的概念和公式后，求解Ax=b，便可直接由得到，分子为使用b替换A中对应列所得到新矩阵的行列式，这便是克拉默法则。遗憾的是，虽然克拉默法则在数学上非常精妙，但因为其庞大的计算量，在工程上用处不大。另外，行列式还有一个巧妙的几何解释，即行列式的值等于向量空间中对应向量围成的体积。例如，若矩阵A是正交矩阵，它是通过单位矩阵立方体旋转得到。

6、特征值和特征向量：本课主要讨论特征值和特征向量的计算。若存在 λ ，使得 A·x=λ·x ，则称 λ 为矩阵A的特征值，x为特征值对应的特征向量。它的几何意义在于，使用矩阵A所对应的线性变换对向量空间中的x作处理，得到的结果与原始向量x共线。因为特征向量非零，所以 A-\lambda·I 是奇异矩阵， |A-λ·I|=0 求出特征值，再将 λ 回代入奇异矩阵，求解对应的零空间的基向量，即为特征向量。同时，矩阵 A+t·I 的特征向量与A相同，对应的特征值全部加t。最后，若矩阵越接近对称，其特征值就越偏向实数，相反，若矩阵是反对称的，特征值就是纯虚数。最后，λ 求和=tr(A)，λ 求积=|A|。

7、对角化和A的幂：特征值和特征向量最明显的作用就是将矩阵对角化。对于矩阵A，将其n个线性无关的特征向量按列构成矩阵S，对A·S=S·V，有 S^{-1}·A·S=V 。V是以对应特征值组成的对角矩阵。最终A的k次幂，即 (A^k)=S·(V^k)·S^{-1} 。于是就引出定理，当K趋近于无穷时，若 |λ| <1 ，A的k次幂趋向于0。更进一步，对于差分方程U(k+1)=A·U(k)，在给定U(0)后，U(k+1)等于多少？递推差分方程，得到 U(k)=(A^k)·U(0) 。因为U(0)是n维向量，所以它一定是n个线性无关的n维特征向量的线性组合，即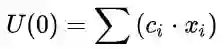，利用这一点，问题不仅被转化为求解A的特征值与特征向量，同时还避免了繁复的矩阵求逆与矩阵相乘问题。该差分方程最简单的应用就是使用线性代数的方法求解斐波那契数列问题。

8、微分方程与exp(At)：本节首先使用线性代数的方法求解通解为 exp(λ·t) 的微分方程。在求解过程中，注意到对于奇异矩阵A，即|A|=0，一定存在特征值0，特征向量即为Ax=0零空间的基。对通解为 exp(λ·t) 的方程解，若特征值的实数部分均<0，则U(t)趋近于0，称为Stability；若存在某一特征值=0，同时其他特征值实数部分均<0，则U(t)趋向于特定值，称为Steady State。若所有特征值实数部分均>0，则方程解发散。

同样，线性代数求解微分方程也可以使用差分方程的思想，将微分方程改写为特征值矩阵V和特征向量矩阵S的形式将其对角化解耦，引出微分方程解的exp(At)形式。最后，对exp(At)泰勒级数展开，证明 exp(At)=S·exp(V·t)·S^{-1} 。

9、马尔科夫矩阵与傅里叶级数：马尔科夫矩阵理论是前文对于差分方程U(k+1)=A·U(k)讨论的一个应用衍生。马尔科夫矩阵中所有元素值均>0，同时矩阵中每一列的和为1，即矩阵的列元素均表示状态转移的概率。于是，对于马尔科夫矩阵有2点关键：①存在一个特征值 λ 为1；②其他所有 |λ| 均<1。于是，当t趋近于无穷大时,U(k)趋近于c1*x1，x1对应特征值为1的特征向量。因此，马尔科夫矩阵常被用来求解Steady State问题。傅里叶级数理论才可参考标准正交基的投影问题，对于Rn空间中的任意n维向量，均可表示为标准正交基的线性组合，推演到函数领域，则任意函数均可使用标准正交的三角函数线性表示，即傅里叶级数！类比向量点积为相乘分量的加总和，这里定义三角函数的内积为两个函数乘积在 [0,2π] 间的定积分。最后，傅里叶级数的系数公式也的确也可以用标准正交基的方式来解释。

10、对称矩阵和正定性：特征值和特征向量是快速了解矩阵的方式，就实对称矩阵来说，它的特征值均为实数，对应的特征向量相互正交。因此，对一般矩阵A，若其n个特征向量线性无关，一定有 A=S·V·S^{-1} ，其中S为特征向量组成的矩阵，V则是由特征值构成的对角矩阵。特别的，若A是对称矩阵，相互正交的特征向量则构成正交矩阵Q，一定有 A= Q·V·Q^{-1}=Q·V·Q^T ，在数学上称之为谱定理，力学上是主轴定理。同时，教授引出复数矩阵来证明实对称矩阵特征值的实数性，对 A·x=λ·x 左右两边同时取共轭，等式仍然成立，由此，再结合对称矩阵的性质可得 λ 的共轭= λ 本身，问题得证。需要注意的是，A*A共轭=实部和虚部的平方和，向量X·X共轭= |X|^2 ，这在复数矩阵中非常重要。最后，对称矩阵中主元的符号与特征值符号相同，即正主元的个数=正特征值的个数。

11、复数矩阵与快速傅里叶变换：设向量z属于n维复空间Cn，有 |z|^2 =共轭 z^T·z ，同理复实数矩阵A=共轭 A^T ，对正交复矩阵Q而言，共轭 Q^T·Q=I 。n阶傅里叶矩阵 F^n = [1,w^i,w^{2i},...,w^{(n-1)i}] ，其中 w^i 表示w的i次幂，i从0开始。在 F^n 中定义 w^n=1 ，则w是1的n次方根，有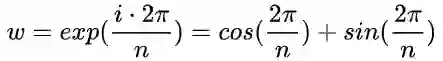，所以w就落在复数平面的单位圆上，同时列向量间相互正交，注意，正交复向量定义为共轭 q^T·q=0 。最终， F^{64} 可以通过 F^{32} 和奇偶置换矩阵以及[(I,D),(I,-D)]相乘来表示,D为关于 w^i 的对角矩阵。再对 F^{32} ， F^{16} …采取相同的操作，逐步迭代，得到快速傅里叶变换FFT使得n阶矩阵相乘的操作从 n^2 下降到n*log2(n)，改进巨大。

12、正定矩阵与最小值：正定矩阵是一类特殊的对称矩阵，它所有的特征值全部为正，其对应的任意阶子矩阵的行列式全都大于0。标准定义为，对任意向量x，若有 x^T·A·x>0 ，则A为正定矩阵。为验证正定的准确性，可以将前者使用二次方程显示表达，然后配方，可将二次方程表示为n个平方项的和，若x非零，A必正定。另外，从微积分求解最小值的角度来看，由于其海森矩阵正定，利用梯度等于0可求得最小值，若最小值>=0，原矩阵A必正定，并且二次方程一定是一个开口向上的碗形曲面，每一个横切面均为椭图形，其中椭图形各长短轴长度即为A的特征值，方向由特征向量决定。最后，正定矩阵来源于最小二乘法，现实中大多数A都是长方形矩阵，若A的列向量线性无关，则 A^T·A 正定，若去除线性无关假设，即为半正定。

13、相似矩阵与若当标准型：前文提到，若矩阵A有n个线性无关的特征向量，则可以使用特征向量矩阵S将A对角化，即 A=S·V·S^{-1} ，V是由特征值构成的对角矩阵。特别的，若A是对称矩阵 A=A^T ，则S为正交矩阵，列向量相互正交， A=S·V·S^T 。更一般的，若存在某一可逆矩阵M，使得 A=M·B·M^T ，则称A与B互为相似矩阵，相似矩阵拥有相同的特征值，但特征向量可能并不相同。另外，由特征值相同引出两大类矩阵，其一为特征值构成的对角矩阵，第二就是若当标准型矩阵，若当标准型是个上三角形矩阵，它是相似矩阵族中除对角元素以外形式最好的矩阵，若当标准化的作用就是，对于一类无法对角化的矩阵来说，可以通过某种方法完成近似对角化，分块矩阵对角线上每个矩阵块均为拥有线性无关特征向量对应的特征值所代表的一个矩阵，即，若当矩阵块的个数与线性无关特征向量的个数相同。

14、奇异值分解：矩阵的奇异值分解是指对任意矩阵A均可分解成2个正交矩阵与1个对角矩阵的乘积，即 A=U·E·V^T 。对称矩阵对角化就是一种特殊的奇异值分解，但普通矩阵对角化则不是。事实上，奇异值分解是将(行空间+零空间)中的一组标准正交基V通过矩阵A，变换至(列空间+左零空间)中的另一组标准正交基U。标准正交基的选取可以首先选定一组线性无关基，然后通过Gram-Smith正交化来实现。即，A·V=U·E，A是变换矩阵，E是由伸缩因子组成的对角矩阵，得到 A=U·E·V^T 。具体到SVD的做法，取 A^T·A 求解其特征值和特征向量，得到对应的E和V，特征值是伸缩因子的平方，或者，取 A·A^T ，同样求解其特征值和特征向量，得到E和U。事实上，若V和U中任意确定一个，其对应的U和V也就随之确定，因此上述方法只需要二选一即可，不能同时使用。

15、线性变换与对应矩阵：每个线性变换都对应一个矩阵，因为前面所学的所有内容都源于矩阵，而矩阵又来源于线性变换，所以线性代数中的线性指的就是线性变换。线性变换必须满足加法定律和数乘定律，例如投影，旋转和导数。通常，线性变换用于一组基V向另一组基U的变换，若将基看作线性空间内的坐标，则原向量a在基V上的坐标a1就被变换至基U上的a2，需要指出的是，向量a在基上的坐标a1,a2就是以基V和U构成的线性组合系数。既然说到坐标，自然就引出的矩阵，矩阵就是基于坐标系和坐标来表示线性变换。最后就是如何根据线性变换T求解其对应的矩阵A，通常的方法是，将线性变换T分别作用到基V中的向量vi上，再分别将作用后的结果表示为基U中所有向量ui上的线性组合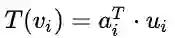，，ai即为矩阵A的第i列。注意，本课主要研究的是在同一组基下的线性变换。

16、基变换和图像压缩：基变换是更一般化的线性变换，通常用于图像压缩，图像压缩本质上先将图像按块划分成n*n的小矩阵，组成R(n*n)维向量，随后选取一组基U，将原始图像表示为标准基V上的坐标至新基U上的坐标，视为线性变换，用矩阵表示为U·x=I·y，y为标准基上的原始坐标，U是由新基为列组成的变换矩阵，则x就是y在U的列空间中的新坐标，即为 x=U^{-1}·y 。然后再去掉一些代表噪声或者不重要的基向量所对应坐标，实现特征选取。最后再反推至原始基上实现图像压缩。对图像压缩来说，最重要的就是基U的选取，需要满足快速求逆和压缩性良好，快速求逆表示基向量矩阵需要能快速求逆，而压缩性良好则表示选取的基要能明确且平稳的表示信号至噪声的过渡。所以，通常会选择傅里叶矩阵(JPEG)和小波矩阵(JPEG2000)作为基的选取。傅里叶矩阵求逆可以由快速傅里叶变换来完成，而小波矩阵本身即为标准正交矩阵，矩阵逆直接对应矩阵转置，同样满足。而压缩性良好方面，2个矩阵均值需要少量的基向量即可表示原图像。理论上，最优的一组基应为一组特征向量基，即 T(v_i)=\lambda_i·v_i ，则对应的变换矩阵A就是特征值构成的对角矩阵，但大数据量的特征值和特征向量计算困难，傅里叶或小波矩阵就是权衡下的最优选择。最后，回到线性代数上来，对于一个给定的线性变换T，将一个标准基下的坐标向量a表示为基V对应坐标所使用的矩阵A相似于基U对应坐标所使用的矩阵B。

17、左右逆和伪逆：当方阵A满秩，即r=m=n时，通常可以求解A逆使得 A·A^{-1}=A^{-1}·A=I 。但现实中遇到的矩阵经常是长方形矩阵，这时就需要考虑3种情况，列满秩r=n，行满秩r=m与一般秩r<n&&r<m。当矩阵A列满秩时， [(A^T·A)^{-1}·A^T]=A 左逆，即A左逆·A=I，值得注意的是，A·A左逆=将任意m维向量投影至A列空间的投影矩阵。同理，当A行满秩时， [A^T·(A·A^T)^{-1}]=A 右逆，A·A右逆=I，A右逆·A=将任意n维向量投影至A行空间的投影矩阵。更一般的，若r<m&&r<n，则只能求A伪逆，A伪逆可以使A行空间向量一一映射至A列空间向量，A伪逆可以通过SVD来解决，SVD可以将对A伪逆的求解转化到求对角阵E的伪逆上来。

18、观后感：MIT线性代数至此就全部学完了，从章节标题的安排上就不难看出，该课程与国内线性代数教材安排完全不同，教授在课堂上的讲解也是深入浅出，有种线性代数三观被刷新的感觉，机器学习预备内容的短板也填补圆满，可以愉快地开始新的机器学习生涯啦！

RECOMMEND

推荐阅读

博客 | 机器学习中的数学基础（实战SVM）

博客 | 机器学习中的数学基础（凸优化）

博客 | 机器学习中的数学基础（线性代数）

博客 | 机器学习中的数学基础（微积分和概率统计）

博客 | 机器学习中的数学基础（概论）

博客 | 一次LDA的项目实战(附GibbsLDA++代码解读）