正态分布为什么常见？

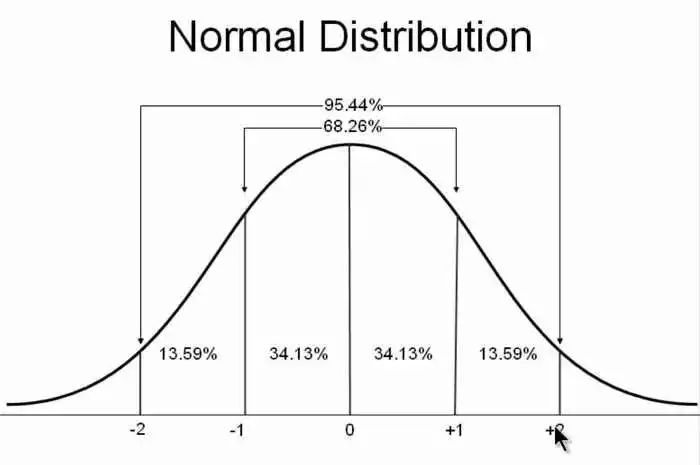
统计学里面，正态分布（normal distribution）最常见。男女身高、寿命、血压、考试成绩、测量误差等等，都属于正态分布。

>>>> 

作者： 阮一峰

以前，我认为中间状态是事物的常态，过高和过低都属于少数，这导致了正态分布的普遍性。最近，读到了 John D. Cook 的文章，才知道我的这种想法是错的。

正态分布为什么常见？真正原因是中心极限定理（central limit theorem）。

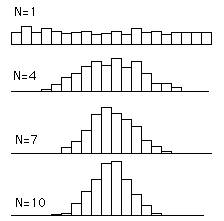
"多个独立统计量的和的平均值，符合正态分布。"

上图中，随着统计量个数的增加，它们和的平均值越来越符合正态分布。

根据中心极限定理，如果一个事物受到多种因素的影响，不管每个因素本身是什么分布，它们加总后，结果的平均值就是正态分布。

举例来说，人的身高既有先天因素（基因），也有后天因素（营养）。每一种因素对身高的影响都是一个统计量，不管这些统计量本身是什么分布，它们和的平均值符合正态分布。（注意：男性身高和女性身高都是正态分布，但男女混合人群的身高不是正态分布。）

许多事物都受到多种因素的影响，这导致了正态分布的常见。

读到这里，读者可能马上就会提出一个问题：正态分布是对称的（高个子与矮个子的比例相同），但是很多真实世界的分布是不对称的。

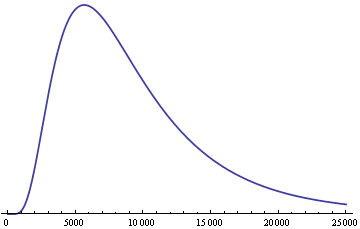
比如，财富的分布就是不对称的，富人的有钱程度（可能比平均值高出上万倍），远远超出穷人的贫穷程度（平均值的十分之一就是赤贫了），即财富分布曲线有右侧的长尾。相比来说，身高的差异就小得多，最高和最矮的人与平均身高的差距，都在30%多。

这是为什么呢，财富明明也受到多种因素的影响，怎么就不是正态分布呢？

原来，正态分布只适合各种因素累加的情况，如果这些因素不是彼此独立的，会互相加强影响，那么就不是正态分布了。一个人是否能够挣大钱，由多种因素决定：

          家庭

          教育

          运气

          工作

           ...

这些因素都不是独立的，会彼此加强。如果出生在上层家庭，那么你就有更大的机会接受良好的教育、找到高薪的工作、遇见好机会，反之亦然。也就是说，这不是 1 + 1 = 2 的效果，而是 1 + 1 > 2。

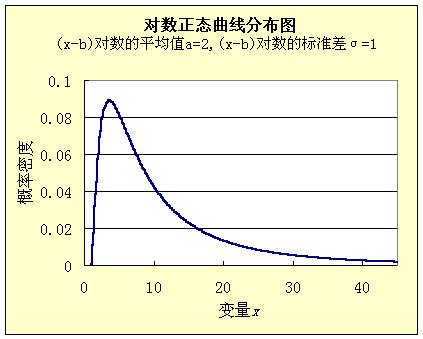
统计学家发现，如果各种因素对结果的影响不是相加，而是相乘，那么最终结果不是正态分布，而是对数正态分布（log normal distribution），即x的对数值log(x)满足正态分布。

这就是说，财富的对数值满足正态分布。如果平均财富是10,000元，那么1000元～10,000元之间的穷人（比平均值低一个数量级，宽度为9000）与10,000元~100,000元之间的富人（比平均值高一个数量级，宽度为90,000）人数一样多。因此，财富曲线左侧的范围比较窄，右侧出现长尾。

参考链接：Why isn't everything normally distributed?，by John D. Cook

（https://www.johndcook.com/blog/2015/03/09/why-isnt-everything-normally-distributed/）

Achievement is not normal,by John D. Cook

（https://www.johndcook.com/blog/2015/03/09/why-isnt-everything-normally-distributed/）

来源：阮一峰的日志

算法数学之美微信公众号欢迎赐稿
稿件涉及数学、物理、算法、计算机、编程等相关领域。
稿件一经采用，我们将奉上稿酬。
投稿邮箱：math_alg@163.com