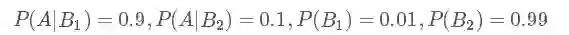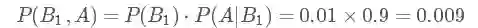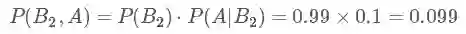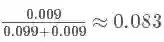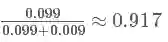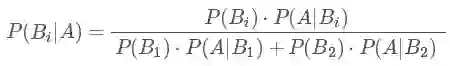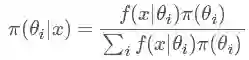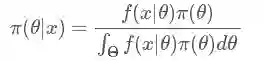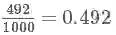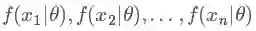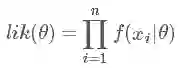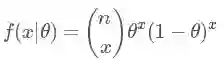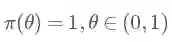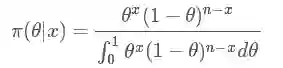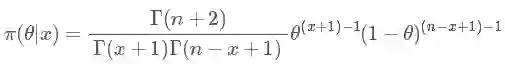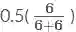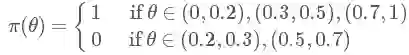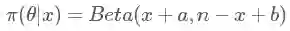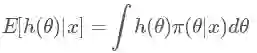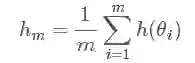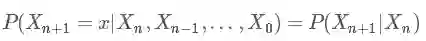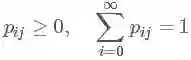浅谈贝叶斯和MCMC

作者 | 徐炎琨

来源 | 徐炎琨的知乎问答

‍‍Abstract：最近课业内的任务不是很多，又邻近暑假了，就在网上搜了一些有关于机器学习和深度学习的课程进行学习。网上的资料非常繁多，很难甄别，我也是货比三家进行学习。这是这个系列的第一个笔记，是关于贝叶斯和MCMC一些数学原理的讲解和代码的实现，希望能够深入浅出，叙述的容易让人理解。…

▌浅谈贝叶斯

不论是学习概率统计还是机器学习的过程中，贝叶斯总是是绕不过去的一道坎，大部分人在学习的时候都是在强行地背公式和套用方法，没有真正去理解其牛逼的思想内涵。我看了一下 Chalmers 一些涉及到贝叶斯统计的课程，content 里的第一条都是 Philosophy of Bayesian statistics。

▌历史背景

什么事都要从头说起，贝叶斯全名为托马斯·贝叶斯(Thomas Bayes，1701-1761),是一位与牛顿同时代的牧师，是一位业余数学家，平时就思考些有关上帝的事情，当然，统计学家都认为概率这个东西就是上帝在掷骰子。当时贝叶斯发现了古典统计学当中的一些缺点，从而提出了自己的“贝叶斯统计学”，但贝叶斯统计当中由于引入了一个主观因素（先验概率，下文会介绍），一点都不被当时的人认可。直到20世纪中期，也就是快200年后了，统计学家在古典统计学中遇到了瓶颈，伴随着计算机技术的发展，当统计学家使用贝叶斯统计理论时发现能解决很多之前不能解决的问题，从而贝叶斯统计学一下子火了起来，两个统计学派从此争论不休。

▌什么是概率？

什么是概率这个问题似乎人人都觉得自己知道，却有很难说明白。比如说我问你 掷一枚硬币为正面的概率为多少？，大部分人第一反应就是50%的几率为正。不好意思，首先这个答案就不正确，只有当材质均匀时硬币为正面的几率才是50%（所以不要觉得打麻将的时候那个骰子每面的几率是相等的，万一被做了手脚呢）。好，那现在假设硬币的材质是均匀的，那么为什么正面的几率就是50%呢？有人会说是因为我掷了1000次硬币，大概有492次是正面，508次是反面，所以近似认为是50%，说得很好（掷了1000次我也是服你）。

掷硬币的例子说明了古典统计学的思想，就是概率是基于大量实验的，也就是 大数定理。那么现在再问你，有些事件，例如：明天下雨的概率是30%；A地会发生地震的概率是 5%；一个人得心脏病的概率是 40%…… 这些概率怎么解释呢？难道是A地真的 100 次的机会里，地震了 5 次吗？肯定不是这样，所以古典统计学就无法解释了。再回到掷硬币的例子中，如果你没有机会掷 1000 次这么多次，而是只掷了 3 次，可这 3 次又都是正面，那该怎么办？难道这个正面的概率就是 100% 了吗？这也是古典统计学的弊端。

举个例子：生病的几率

一种癌症，得了这个癌症的人被检测出为阳性的几率为 90%，未得这种癌症的人被检测出阴性的几率为 90%，而人群中得这种癌症的几率为 1%，一个人被检测出阳性，问这个人得癌症的几率为多少？

猛地一看，被检查出阳性，而且得癌症的话阳性的概率是 90%，那想必这个人应该是难以幸免了。那我们接下来就算算看。

我们用  A表示事件 “测出为阳性”, 用  B 1  表示“得癌症”,  B 2  表示“未得癌症”。根据题目，我们知道如下信息:

那么我们现在想得到的是已知为阳性的情况下，得癌症的几率  P ( B 1 , A )  :

P ( B 1 , A )  表示的是联合概率，得癌症且检测出阳性的概率是人群中得癌症的概率乘上得癌症时测出是阳性的几率，是 0.009。同理可得得癌症且检测出阳性的概率：

这个概率是什么意思呢？其实是指如果人群中有 1000 个人，检测出阳性并且得癌症的人有 9 个，检测出阳性但未得癌症的人有 99 个。可以看出，检测出阳性并不可怕，不得癌症的是绝大多数的，这跟我们一开始的直觉判断是不同的！可直到现在，我们并没有得到所谓的“在检测出阳性的前提下得癌症的 概率 ”，怎么得到呢？很简单，就是看被测出为阳性的这 108(9+99) 人里，9 人和 99 人分别占的比例就是我们要的,也就是说我们只需要添加一个归一化因子(normalization)就可以了。所以阳性得癌症的概率 P ( B 1 | A )  为：

 阳性未得癌症的概率  P ( B 2 | A )  为：

这里  P ( B 1 | A )  ， P ( B 2 | A )  中间多了这一竖线 | | 成为了条件概率，而这个概率就是贝叶斯统计中的后验概率！而人群中患癌症与否的概率  P ( B 1 ) , P ( B 2 )  就是先验概率！我们知道了先验概率，根据观测值(observation)，也可称为 test evidence：是否为阳性，来判断得癌症的后验概率，这就是基本的贝叶斯思想，我们现在就能得出本题的后验概率的公式为：

由此就能得到如下的贝叶斯公式的一般形式。

▌贝叶斯公式

我们把上面例题中的  A 变成样本(sample)  x  , 把 B  变成参数(parameter)  θ , 我们便得到我们的贝叶斯公式：

‍‍可以看出上面这个例子中， B  事件的分布是离散的，所以在分母用的是求和符号  ∑  。那如果我们的参数  θ  的分布是连续的呢？没错，那就要用积分，于是我们终于得到了真正的贝叶斯公式 ：

其中 π 指的是参数的概率分布，π(θ) 指的是先验概率，π(θ|x) 指的是后验概率，f(x|θ)指的是我们观测到的样本的分布，也就是似然函数(likelihood)，记住竖线 |左边的才是我们需要的。其中积分求的区间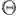指的是参数 θ 所有可能取到的值的域，所以可以看出后验概率 π(θ|x) 是在知道 x 的前提下在域内的一个关于θ 的概率密度分布，每一个θ 都有一个对应的可能性(也就是概率)。

▌理解贝叶斯公式

这个公式应该在概率论书中就有提到，反正当时我也只是死记硬背住，然后遇到题目就套用。甚至在 Chalmers 学了一门统计推断的课讲了贝叶斯，大部分时间我还是在套用公式，直到后来结合了一些专门讲解贝叶斯的课程和资料才有了一些真正的理解。要想理解这个公式，首先要知道这个竖线 | 的两侧一会是 x|θ ，一会是 θ|x 到底指的是什么，或者说似然函数和参数概率分布到底指的是什么。

▌似然函数

首先来看似然函数 f(x|θ)，似然函数听起来很陌生，其实就是我们在概率论当中看到的各种概率分布 f(x)，那为什么后面要加个参数|θ 呢？我们知道，掷硬币这个事件是服从伯努利分布的 Ber(p) , n次的伯努利实验就是我们熟知的二项分布 Bin(n,p), 这里的p就是一个参数，原来我们在做实验之前，这个参数就已经存在了(可以理解为上帝已经定好了)，我们抽样出很多的样本 x 是为了找出这个参数，我们上面所说的掷硬币的例子，由于我们掷了 1000 次有 492 次是正面，根据求期望的公式 n⋅p=μ (492就是我们的期望)可以得出参数 p 为 

所以我们才认为正面的概率是近似 50% 的。

现在我们知道了，其实我们观测到样本 x 的分布是在以某个参数 θ 为前提下得出来的，所以我们记为 f(x|θ)，只是我们并不知道这个参数是多少。所以参数估计成为了统计学里很大的一个课题，古典统计学中常用的方法有两种：矩方法(momnet)和最大似然估计(maximum likelihood estimate, mle) ，我们常用的像上面掷硬币例子中求均值的方法，本质就是矩估计方法，这是基于大数定理的。而统计学中更广泛的是使用最大似然估计的方法，原理其实很简单，在这简单说一下：假设我们有 n 个样本 x1,x2,x3,…,xn，它们每一个变量都对应一个似然函数:

我们现在把这些似然函数乘起来:

我们只要找到令 lik(θ)  这个函数最大的 θ 值，便是我们想要的参数值(具体计算参考[2]中p184)。

▌后验分布(Posterior distribution)

现在到了贝叶斯的时间了。以前我们想知道一个参数，要通过大量的观测值才能得出，而且是只能得出一个参数值。而现在运用了贝叶斯统计思想，这个后验概率分布 π(θ|x) 其实是一系列参数值 θ 的概率分布，再说简单点就是我们得到了许多个参数 θ 及其对应的可能性，我们只需要从中选取我们想要的值就可以了：有时我们想要概率最大的那个参数，那这就是 后验众数估计(posterior mode estimator)；有时我们想知道参数分布的中位数，那这就是后验中位数估计(posterior median estimator);有时我们想知道的是这个参数分布的均值，那就是后验期望估计。这三种估计没有谁好谁坏，只是提供了三种方法得出参数，看需要来选择。现在这样看来得到的参数是不是更具有说服力？

▌置信区间和可信区间

在这里我想提一下置信区间(confidence interval, CI) 和可信区间(credibility interval,CI),我觉得这是刚学贝叶斯时候非常容易弄混的概念。

再举个例子：一个班级男生的身高可能服从某种正态分布 N(μ,σ2),然后我们把全班男生的身高给记录下来，用高中就学过的求均值和方差的公式就可以算出来这两个参数，要知道我们真正想知道的是这个参数 μ,σ2，当然样本越多，得出的结果就接近真实值(其实并没有人知道什么是真实值，可能只有上帝知道)。等我们算出了均值和方差，我们这时候一般会构建一个95%或者90%的置信区间，这个置信区间是对于样本 x 来说的，我只算出了一个 μ 和 一个 σ 参数值的情况下，95% 的置信区间意味着在这个区间里的样本是可以相信是服从以 μ,σ 为参数的正态分布的，一定要记住置信区间的概念中是指一个参数值的情况下！

而我们也会对我们得到的后验概率分布构造一个 90% 或 95% 的区间，称之为可信区间。这个可信区间是对于参数 θ 来说的，我们的到了 很多的参数值，取其中概率更大一些的90%或95%，便成了可信区间。

▌先验分布(Prior distribution)

说完了后验分布，现在就来说说先验分布。先验分布就是你在取得实验观测值以前对一个参数概率分布的主观判断，这也就是为什么贝叶斯统计学一直不被认可的原因，统计学或者数学都是客观的，怎么能加入主观因素呢？但事实证明这样的效果会非常好！

再拿掷硬币的例子来看(怎么老是拿这个举例，是有多爱钱。。。)，在扔之前你会有判断正面的概率是50%，这就是所谓的先验概率，但如果是在打赌，为了让自己的描述准确点，我们可能会说正面的概率为 0.5 的可能性最大，0.45 的几率小点，0.4 的几率再小点，0.1 的几率几乎没有等等，这就形成了一个先验概率分布。

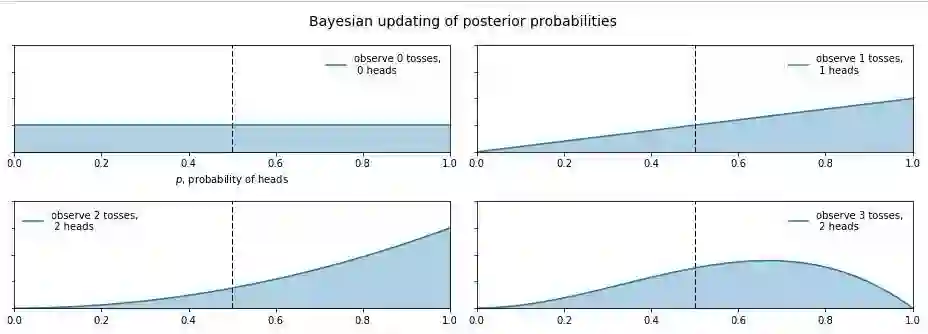
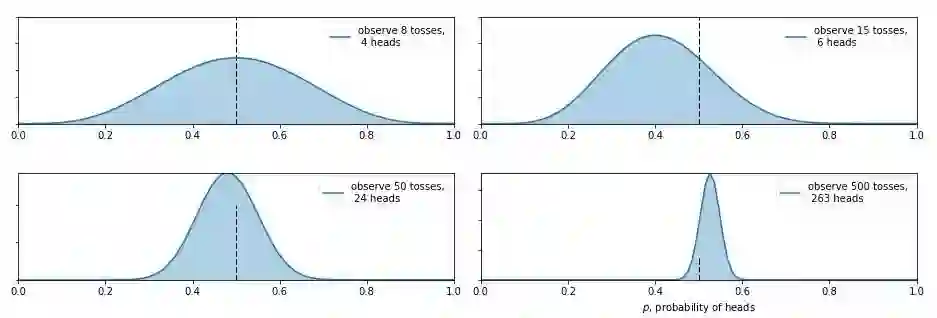
那么现在又有新的问题了，如果我告诉你这个硬币的材质是不均匀的，那正面的可能性是多少呢？这就让人犯糊涂了，我们想有主观判断也无从下手，于是我们就想说那就先认为 0~1 之间每一种的可能性都是相同的吧，也就是设置成 0~1 之间的均匀分布Uni(0,1) 作为先验分布吧，这就是贝叶斯统计学当中的无信息先验(noninformative prior)！那么下面我们就通过不断掷硬币来看看，这个概率到是多少，贝叶斯过程如下：

从图中我们可以看出，0 次试验的时候就是我们的先验假设——均匀分布，然后掷了第一次是正面，于是概率分布倾向于 1，第二次又是正，概率是 1的可能性更大了，但注意：这时候在 0.5 的概率还是有的，只不过概率很小，在 0.2 的概率变得更小。第三次是反面，于是概率分布被修正了一下，从为1的概率最大变成了 2/3 左右最大(3次试验，2 次正 1 次反当然概率是2/3的概率最大)。再下面就是进行更多次的试验，后验概率不断根据观测值在改变，当次数很大的时候，结果趋向于 0.5 (哈哈，结果这还是一枚普通的硬币，不过这个事件告诉我们，直觉是不可靠的，一定亲自实验才行~)。

有的人会说，这还不是在大量数据下得到了正面概率为 0.5 嘛，有什么好稀奇的？注意了！画重点了！(敲黑板) 记住，不要和一个统计学家或者数学家打赌！跑题了，跑题了。。。说回来，我们上面就说到了古典概率学的弊端就是如果掷了 2 次都是正面，那我们就会认为正面的概率是 1，而在贝叶斯统计学中，如果我们掷了 2 次都是正面，只能说明正面是1的可能性最大，但还是有可能为 0.5, 0.6, 0.7 等等的，这就是对古典统计学的一种完善和补充，于是我们也就是解释了，我们所谓的地震的概率为 5%；生病的概率为 10% 等等这些概率的意义了，这就是贝叶斯统计学的哲学思想。

▌共轭先验(Conjugate prior)

共轭先验应该是每一个贝叶斯统计初学者最头疼的问题，我觉得没有“之一”。这是一个非常大的理论体系，我试着用一些简单的语言进行描述，关键是去理解其思想。

继续拿掷硬币的例子，这是一个二项试验 Bin(n,p)，所以其似然函数为:

在我们不知道情况时就先假设其先验分布为均匀分布 Uni(0,1)，即：

那现在根据贝叶斯公式求后验概率分布：

我们得到结果为:

这么一大串是什么呢？其实就是大名鼎鼎的贝塔分布(Beta distribution)。 简写就是 Be(x+1,n−x+1)。 比如我掷了10 次(n=10)，5次正(x=5),5 次反，那么结果就是 Be(6,6), 这个分布的均值就是

很符合我们想要的结果。

现在可以说明，我们把主观揣测的先验概率定为均匀分布是合理的，因为我们在对一件事物没有了解的时候，先认为每种可能性都一样是非常说得通的。有人会认为，既然无信息先验是说得通的，而且贝叶斯公式会根据我们的观测值不断更新后验概率，那是不是我们随便给一个先验概率都可以呢？当然……不行！！这个先验概率是不能瞎猜的，是需要根据一些前人的经验和常识来判断的。比如我随便猜先验为一个分段函数：

靠，是不是很变态的一个函数…就是假设一个极端的情况，如果你把这个情况代入贝叶斯公式，结果是不会好的(当然我也不知道该怎么计算)。

这个例子中，我看到了可能的后验分布是 Beta 分布，看起来感觉有点像正态分布啊，那我们用正态分布作为先验分布可以吗？这个是可以的(所以要学会观察)。可如果我们把先验分布为正态分布代入到贝叶斯公式，那计算会非常非常麻烦，虽然结果可能是合理的。那怎么办？不用担心，因为我们有共轭先验分布！

继续拿上面这个例子，如果我们把先验分布 π(θ) 设为贝塔分布 Beta(a,b)，结果是什么呢？我就不写具体的计算过程啦，直接给结果：

有没有看到，依然是贝塔分布，结果只是把之前的 1 换成了 a 和 b(聪明的你可能已经发现，其实我们所说的均匀分布 Uni(0,1) 等价于 Beta(1,1),两者是一样的)。

由此我们便可以称二项分布的共轭先验分布为贝塔分布！注意！接着画重点！：共轭先验这个概念必须是基于似然函数来讨论的，否则没有意义！好，那现在有了共轭先验，然后呢？作用呢？这应该是很多初学者的疑问。

现在我们来看，如果你知道了一个观测样本的似然函数是二项分布的，那我们把先验分布直接设为 Beta(a,b) ，于是我们就不用计算复杂的含有积分的贝叶斯公式便可得到后验分布 Beta (x+a,n−x+b) 了！！！只需要记住试验次数n，和试验成功事件次数x就可以了！互为共轭的分布还有一些，但都很复杂，用到的情况也很少，推导过程也极其复杂，有兴趣的可以自行搜索。我说的这个情况是最常见的！

注意一下，很多资料里会提到一个概念叫伪计数(pseudo count),这里的伪计数值得就是a,b对后验概率分布的影响，我们会发现如果我们取 Beta(1,1) ，这个先验概率对结果的影响会很小，可如果我们设为 Beta(100,100)，那么我们做 10 次试验就算是全是正面的，后验分布都没什么变化。

▌朴素贝叶斯分类器(Naive Bayes classifier)和scikit-learn的简单使用

在机器学习中你应该会看到有一个章节是讲朴素贝叶斯分类器的(把naive翻译成朴素我也是服了啊，以后我们可以“夸”某某人好朴素啊)。具体的数学原理在周志华老师的西瓜书《机器学习》的第7章有详细解释，其实就是利用了基本的贝叶斯理论，跟上面说的差不多，只不过更加说明的怎样去实践到机器学习中。下面就直接简单说一下Python中有个机器学习库 scikit-learn 中朴素贝叶斯分类器的简单实用。例子参考的是 scikit-learn 官网的GaussianNB 页面。

直接看代码：

import numpy as np
X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
Y = np.array([1, 1, 1, 2, 2, 2])
from sklearn.naive_bayes import GaussianNB #导入GaussianNB
clf = GaussianNB() #设置clf为高斯朴素贝叶斯分类器
clf.fit(X, Y) #训练数据
print(clf.predict([[-1, 0]])) #预测数据[-1,0]属于哪一类

输出结果为: [1]。 这里面我们可以看到有 X,Y 两个变量，X是我们要训练的数据特征，而Y给的是对应数据的标签，分成 [1],[2] 两类。用 clf.fit 训练好了之后，用 clf.predict 预测新数据[-1,0]，结果是被分为第一类，说明结果是令人满意的。

MCMC(Markov chain Monte Carlo)

你以为说到这贝叶斯的事情就结束了？那你真的就是太 naive 了。贝叶斯公式里的 θ 只是一个参数，有没有想过有两个参数怎么办？还能怎么办，分布的积分改成双重积分呗。可以可以，那如果有 3个、5个、10 个参数呢？还有十重积分嘛？很显然积分这个工具只适合我们在一维和二维的情况下进行计算，三维以上的效果就已经不好了；其实不仅仅在于多维情况，就算是在一维情况很多积分也很难用数值方法计算出来，那该怎么办？于是便有了 MCMC 方法，全称是马尔科夫链蒙特卡洛方法。大家别指望在下文里看到详细的计算过程和推导，我还是按照我的理解，简单地从原理出发进行描述，让大家有一个感性的认识。

第二个MC：蒙特卡洛方法

虽然蒙特卡洛方法是 MCMC 中的第二个 MC，但先解释蒙特卡洛方法会更加容易理解。蒙特卡洛方法也称蒙特卡洛抽样方法，其基本思想是通过大量取样来近似得到想要的答案。有一个经典的试验就是计算圆周率，在一个边上为1的正方形中画一个内切圆，圆的面积就是 π，圆面积比上整体的正方形面积也是 ππ, 现在在正方形内产生大量随机数，最后我们只需要计算在圆内点的个数比上总体点的个数，便近似得到了圆周率 π 的值(这些统计学家是真聪明啊。。。)。

现在回到贝叶斯公式，我们现在有一个后验概率 π(θ|x) ，但我们其实最想知道的是 h(θ) 的后验期望：

怎么又跑出来一个 h(θ) ？不要着急，如果我们令 h(θ)=θ , 那上面这个积分求得就是我们想要的后验期望估计了！(当然 h(θ) 还可以是其他情况，会得到其他我们想要的结果，例如后验最大估计，后验方差等等，这里就不赘述了) 蒙特卡洛方法指出：如果我们可以从后验概率分布 π(θ|x) 中抽取大量的独立同分布(i.i.d)的观测值 θ1,θ2,…,θm ,于是我们可以用如下公式：

在大数定理的支持下，hm 就可看作是 E[h(θ)|x] 的近似值。但是这个方法在多维和后验分布形式未知的情况下，很难抽样，于是便有了第一个 MC，马尔科夫链的方法。

第一个MC：马尔科夫链

马尔科夫链也称之为马氏链，先来看一下数学定义：

意思就是，从 Xn,Xn−1,…,X0 到 Xn+1 的转移概率只与 Xn+1 的前一个状态 Xn 有关。

如果条件概率 P(Xn+1|Xn) 与 n 无关，成为一个固定值，那么就称这个马氏链有平稳转移概率，记为 pij 。并且我们称 P=(pij) 为马氏链的转移矩阵，且满足条件：

怎么一个概率变成一个矩阵了？？？其实这个转移概率 pij 指的只是状态 i 中的一个观测值 Xn 到状态 j 中的另一个观测值 Xn+1 的概率，其实我们在每个状态下许许多多的观测值。我随便举一例子：

现有一个转换矩阵：

可以看出状态 i 中的一个观测值转移到下个状态 j 的分别三个观测值的概率和为1。

下面就是最最重要的马氏链的平稳性(也可称之为收敛性)：

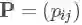
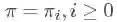
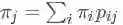
设马尔科夫链有转移概率矩阵, 一个概率分布如果满足 ，则称之为此马尔科夫链的平稳分布。（取自[1]中定义6.3.2）

可能这么看这个定义还是有点绕，这里的 i,j 并不是指从 i 一步就到了 j ,求和符号 ∑ 的意思就是能让概率分布 π(i) 经过 n 步之后成为平稳分布 π(j) 。我们得到的平稳分布 π(j)=[π(1),π(2),…,π(j)] 里面各个概率的和也为1。

现在我们就要把这个马尔科夫链和贝叶斯联系起来，按照我的理解，π(i) 就是我们的先验分布，如果我们能找到一个转移矩阵，那么我们就会在n步之后就会收敛到一个平稳分布，而这个分布就是我们要的后验分布。得到平稳分布后，根据平稳性，继续乘上这个转移概率矩阵，平稳分布依然不会改变，所以我们就从得到平稳分布开始每次对其中抽样 1 个出来，再经过 m 步之后，我们就得到了 m 个服从后验分布的 i.i.d 样本，便可按照第二个 MC 蒙特卡洛方法进行计算了！

当然，还有很多理论是关于如何找这个转移概率矩阵的，和算法如何实现的，但这些都太复杂了，就不在这里说了。MCMC 是一个有着完整体系的东西，市面上都很少有详细介绍其理论过程的资料，有的话那都不是几十页纸能讲完的。有一些很好的讲解可参考资料[1][4]，尤其是[4]是个很有名的文档，讲得非常通俗易懂、深入浅出，我在这两个部分写的少的原因就是如果写多了也就是把这些资料对应部分重新说一遍，所以有兴趣的就直接看这些资料吧。

MCMC 的 Python 实现——Pymc

原本想在这里详细介绍一个例子的，但终究还是别人的例子，还是去看原资料比较好，见[4]。注意文件的文件是 ipython 的格式，用 anaconda 里的 Jupyter notebook 打开就行。还有要注意的是每个章节的内容分为了pymc2 和 pymc3 两个库的实现。pymc3 需要依赖项 theano 才行，我一开始就一直运行不起来，原来 theano 只能在Python<3.6和scipy<0.17.1 才能运行。

▌结尾

这篇文章主要介绍了贝叶斯统计的数学思想，这篇文章从头到尾写了有近十个小时了，希望能对大家有所帮助，如果有任何错误和解释不当的地方，请给我评论，我也只是个初学者，也希望能得到大神的指点。

References

[1]韦来生，《贝叶斯统计》，高等教育出版社，2016

[2]John A.Rice, 《数理统计与数据分析》(原书第三版), 机械工业出版社, 2016

[3]Cameron Davidson-Pilon, Probabilistic Programming and Bayesian Methods for Hackers, 2016

[4]Rickjin(靳志辉)，《LDA数学八卦》，2013

Acknowledge

本篇内容结合了我在炼数成金(dataguru.cn)报的Python机器学习课程以及Udacity里ud-120:机器学习入门课程的讲解，让我对贝叶斯有了一个新的理解和认识，表示感谢。

原文地址：

https://www.zhihu.com/people/xuyankun/activities

（编辑注：文中题图来自sciencenews）

精彩预告

◆

AI公开课

◆

时间：6月14日 20:00-21:00

扫描海报二维码，免费报名

添加微信csdnai，备注：公开课，加入课程交流群

点击 | 阅读原文 | 免费学习