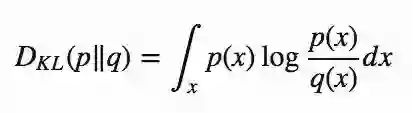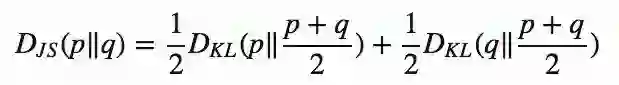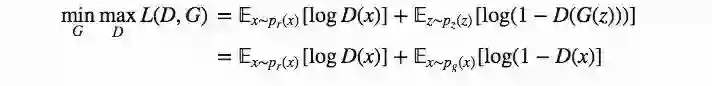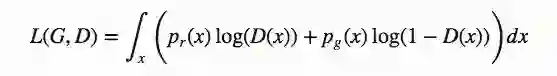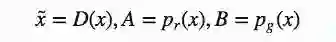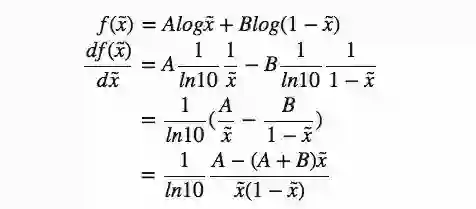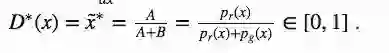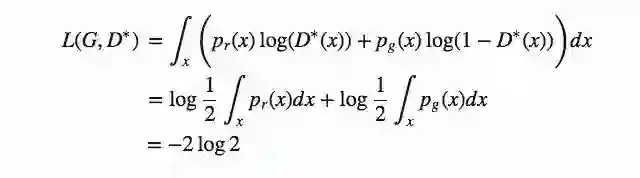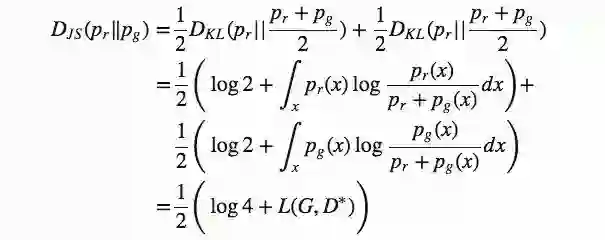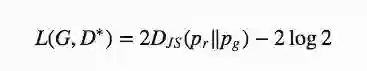从GAN到WGAN：生成对抗网络背后的数学原理（一）

作者： Lilian Weng

编译：Bot

本文解释了生成对抗网络（GAN）背后的数学原理及其难以训练的原因，并指出Wasserstein GAN是通过测量两个概率分部之间的平滑度来改进GAN训练的。

如今，生成对抗网络（GAN）已经取得了不少大型成果，它可以复制真实世界的丰富内容，如图像、语言和音乐等。它受博弈论启发：两个模型，一个生成器，一个判别器，两者在相互竞争的同时又相互扶持、共同进步。但是训练GAN并不是一件容易的事，因为自Ian Goodfellow提出这个概念以来，它就一直存在训练不稳定、容易崩溃的问题。

在这里，我想介绍一下GAN背后的数学原理及其难以训练的原因，并引入2017年FAIR提出的Wasserstein GAN，谈谈它是怎么在数学上实现突破性改进的。

• KL散度和JS散度

• 生成对抗网络（GAN）

• D的最佳值

• 什么是全局最优

• 损失函数代表什么

• GAN的问题

• 很难达成纳什均衡

• 低维支持

• 消失的渐变

• 模式崩溃

• 缺乏一个适当的评估指标

• 改进GAN的训练

• Wasserstein GAN（WGAN）

• 什么是Wasserstein距离

• 为什么Wasserstein比JS、KL发散更好

• 把Wasserstein距离作为GAN的损失函数

• 示例：用GAN生成新的宠物小精灵（pokemon）

• 参考文献

KL散度和JS散度

在开始介绍GAN之前，我们先来回顾这两个描述概率分布差异的概念：KL散度和JS散度。

KL（Kullback-Leibler）散度

KL散度又称相对熵、信息增益，它衡量的是概率分布P和概率分布Q之间的差异。

当p(x) == q(x)时，D_KL达到最小值，也就是0。

从上述公式可以看出，KL散度是不对称的。当p(x)接近0，而q(x)一定不是0时，这个公式会“忽视”q(x)的作用。这导致的结果就是如果概率分布P和Q是两个同等重要的概率分布，KL散度可能会在计算相似性时出现错误。

JS（ Jensen–Shannon）散度

JS散度是另一种衡量概率分布相似度的方式，它基于KL散度的变体，解决了不对称的问题，而且更加平滑。它的计算结果在0—1之间：如果p(x)和q(x)完全相同，那么D_JS等于0；如果完全不同，那就等于1。

图1 给定两个高斯分布，其中p的mean=0，std=1；q的mean=1，std=1。m=(p+q)/2。可以发现D_KL是不对称的，D_JS是对称的

注：当然JS散度也存在缺陷，就是当P和Q距离过远时，D_JS等于0，是个常数，这时梯度消失了。

一些人（Huszar，2015）认为，GAN取得巨大成功的原因之一是把损失函数从KL散度换成了JS散度。对于这个观点，我们会在下一节讨论。

生成对抗网络（GAN）

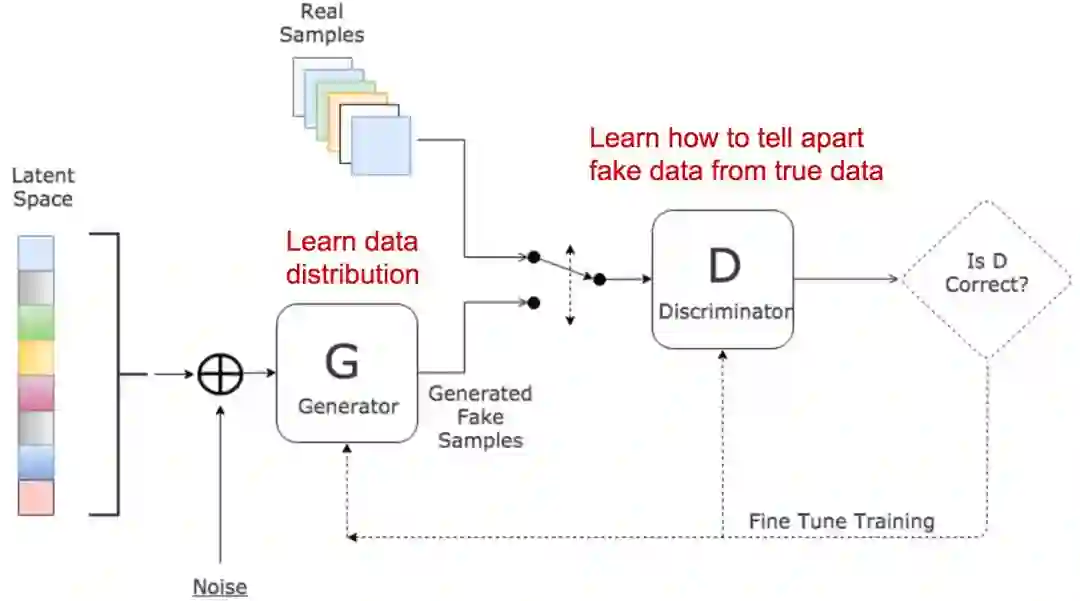
GAN由两个模型组成：

• 判别器D。这个模型负责预测样本来自真实数据集的概率，它在真实数据上训练，学习真实的数据分布，因此能指出生成样本的不足。从某种意义上来说，它像一个批评家；

• 生成器G。这个模型负责将输入的可变噪声信号z合成为新的样本（z包含潜在的真实数据分布），然后输入判别器做判断。它的目标是基于判别器的输出捕捉真实数据分布，使自己生成的样本尽可能逼真。换言之，就是让判别器D输出高概率。

图2 GAN的架构

这两个模型在训练过程中互相竞争：生成器G一直在努力“欺骗”判别器D，判别器则在不断提升自我，避免被骗。正是这种有趣的零和博弈激发了GAN的潜力。

我们设：

符号	含义	注
pz	噪声数据z（输入）的分布	通常是均一的
pg	生成器中数据x的分布	-
pr	真实样本x的分布	-

一方面，我们希望输入真实数据后，判别器D输出的概率尽可能地大，即𝔼_x∼pr(x)[logD(x)]最大；同时，输入生成样本G(z)，z∼pz(z)后，判别器的𝔼_z∼pz(z)[log(1−D(G(z)))]能最大，也就是D(G(z))接近0。

另一方面，我们也希望生成器生成的假样本能使判别器输出高概率，即D𝔼_z∼pz(z)[log(1−D(G(z)))]最小化。

当把这些想法综合到一起，我们就可以发现，其实生成器G和判别器D构成了极大极小博弈，从数学角度看，就是我们要优化这个损失函数：

在梯度下降过程中，(𝔼_x∼pr(x)[logD(x)]对G没有任何影响。

D的最佳值是多少？

现在我们有了一个明确的损失函数。我们先来研究一下D的最佳值：

因为我们要求L(G,D)极大情况下D(x)的最佳值，我们先设定义：

之后是求导（因为x可对所有可能的值采样，所以可以忽略积分）：

当df(x̃)/dx̃=0，我们就能得到D的最佳值：

一旦生成器被训练到最佳状态，p_g就会无限接近p_r，当p_g=p_r，D∗(x)的值就是1/2。

什么是全局最优？

当生成器和判别器都被训练到最佳状态时，p_g=p_r，D∗(x)=1/2，这时我们的损失函数就变成：

损失函数代表什么？

正如我们在第一节中介绍的，p_g和p_r之间的JS散度可以这么算：

也就是：

从本质上来说，当生成器最优时，GAN的损失函数会通过JS散度来量化生成数据分布p_g和实际样本分布p_r之间的相似性。能复现真实样本数据分布的最佳生成器G∗可以使L(G∗,D∗)=−2log2的值最小。

GAN的其他变体：在不同情况下GAN有许多变体，或者设计用于不同的任务。例如，对于半监督学习任务，一个想法是更新判别器以输出实际类别标签：1，...，K-11，...，K-1以及一个假类别标签KK。生成器模型的目标则是欺骗鉴别器，让它输出小于KK的分类标签。

（未完待续……）