【Embedding】GloVe：大规模语料中快速训练词向量

1. Introduction

今天学的论文是斯坦福大学 2014 年的工作《GloVe: Global Vectors for Word Representation》，在当时有两种主流的 Word Embedding 方式，一种是矩阵分解，类似 LSA；另一种是 13 年提出的 Word2Vec，基于滑动窗口的浅层神经网络。前者的优点是利用了全局的统计信息（共现矩阵），后者的优点是计算简单且效果好 = =，但缺点是没利用全局的统计信息。所以这篇论文的主要工作是想综合两者的优点。

在看论文前我们不妨来思考一下，如果你是研究员，现在有这样的想法（综合全局信息和局部信息），你该如何去实现？

2. GloVe Model

2.1 Weighted Least Squares

我们先来给些定义，另 X 为词与词的共现矩阵，  表示单词 j 出现在单词 i 上下文中的次数。于是我们有单词 j 出现在单词 i 上下文的共现概率：

我们观察下表的共现概率，只看第一行第二行我们能看出 ice 和 stream 与 solid gas water fashion 等词的相关性吗？答案是否定的，但如果我们使用比值   就可以很直观的看到其相关性。当 k = solid 时，其值为 8.9，则表明，ice 与 solid 更相关；当 k = gas 时，其值为   ，所以 steam 与 gas 更相关；当值为 1 左右时，表明 ice 和 steam 与目标单词 k 都相关或者都不相关。

Co-occurrence Probabilities

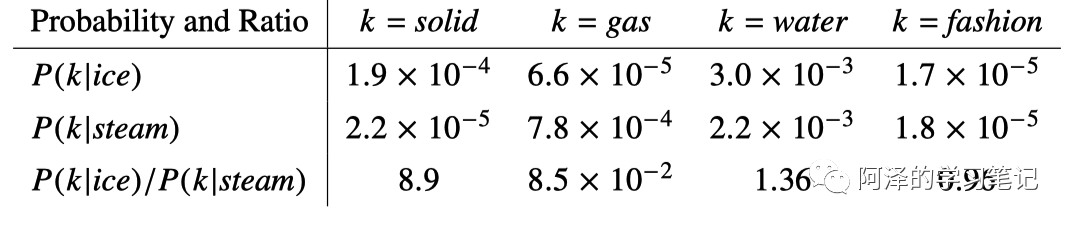
从上面的表述中我们看出，比值更能反映相关性，而不是共现单词概率。所以我们有：

其中，  表示单词 i 的词向量，  是独立的上下文向量将在后面进行介绍，F 可以视为一种映射或是一种运算。

我们再来看下上面的等式，一个很直观的感觉就是 F 可能取值很广。不过不要紧，我们现在给它加些约束。由于向量空间是线形的，所以可以使用向量差：

为了保证混合向量的维度不变，我们再做个点乘：

实际中，单词和共现单词是可以可交换的，现在的等式不满足交换律。

为了保证交换律，我们先让 F 保证为群   到群   的群同态：



群同态：设   和   是两个群， ，有  ，则称   为 M 到 S 的同态或群映射。

”

所以我们有：

从加减到乘除的运算最容易想到的是指数运算，所以  ：

但是有   存在依然没法符合交换律，又由于其与 k 无关，所以可以将其视为一个常数   ：

现在还不满足，不过已经很快了，我们在额外的添加一个偏执项  ：

好了，现在的等式是对原始等式的一个极端简化。但这个等式还有一个问题：当   时怎么办？所以在实际的算法中我们会加一个偏执：  ，这样即保证了稀疏性，又不至于导致发散。

以上想法看似天马行空，其实一部分想法是与 LSA 密切相关的（参考 SVD 的变种）。我们 LSA 所有的共现都是等价的， 即使共现次数非常小。然而很多非常小的共现可能是源于噪声，其携带的信息非常少，所以我们引入加权最小二乘法来约束一下噪声：

其中，权重应该遵循以下原则：

1. ，保证了代价函数 J 在 0 点的连续性；
2.  应该非递减的，这个很好理解，共现越多，权值越大；
3. 对于较大的 x ，  不能太大；

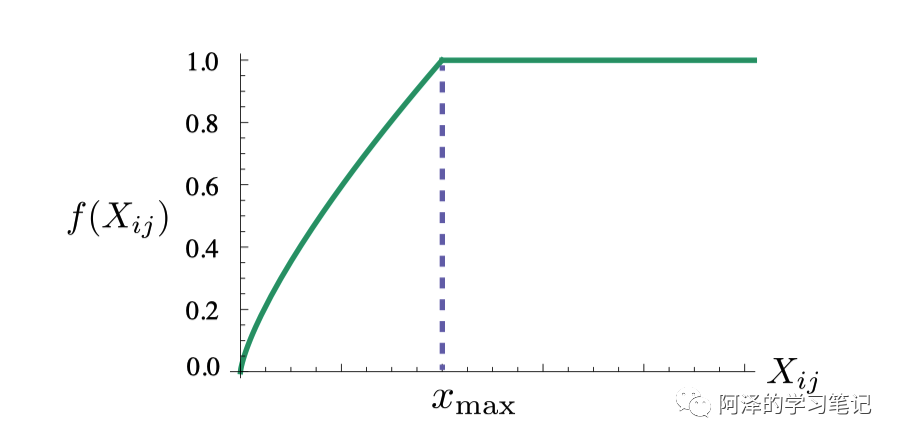
这样的函数有很多，我们自己设计一个：

这里的   为经验参数，可以取 1 或者 3/4，我们这里取 3/4（是不是想起了什么？提示一下：Word2Vec 中 Negative Sampling ）。下图为   的函数的可视化：

Weight Function f

2.2 Relationship to Word2Vec

目前所有的 Word Embedding 的无监督方法最终都是基于语料库的，只是某些方法不是特别明显，如 Word2Vec，本节将说明我们定义的模型与现有模型的一些关系。

我们先来给出 Skip-Gram 的预测概率：

全局交叉熵代价函数为：

计算代价昂贵，Skip-Gram 给出会采用近似解。

由于相同单词 i 和 j 可以在语料库中出现多次，所以将相同值的 i 和 j 放在一起：

由于   ，所以:

其中，  为分布   和   的交叉熵。J 可以视为交叉上误差的加权和。

交叉熵损失的一个重要缺点是需要对分布 Q 进行归一化，代价昂贵，所以我们使用最小二乘法来代替交叉熵：

其中， 都是非正态分布，舍弃原来的归一化因子。

但这个式子引入了一个新的问题：  通常取值很大。一个有效的方式是取 log：

当然 Mikolov 等人也采用了 Sub-Sampling 来减少高频单词的权重，所以我们有：

至此就完成了公式推导，可以看到其实这和我们给出的 GloVe 的代价函数基本是一致的。

3. Experiments

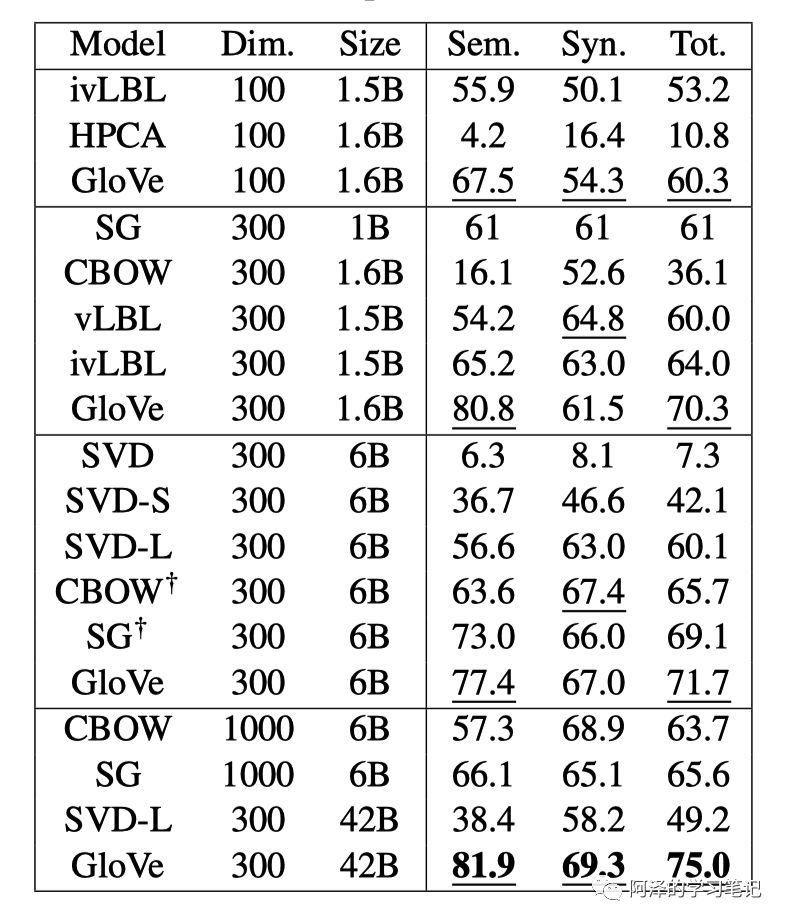
然后我们来看下与其他模型的对比实验部分：

Experiments_1

Experiment

Experiments

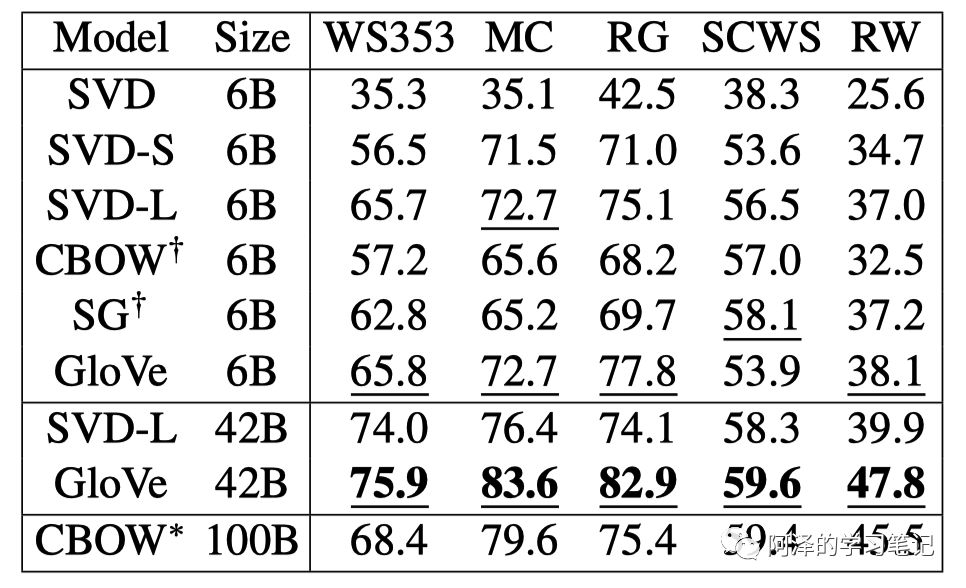
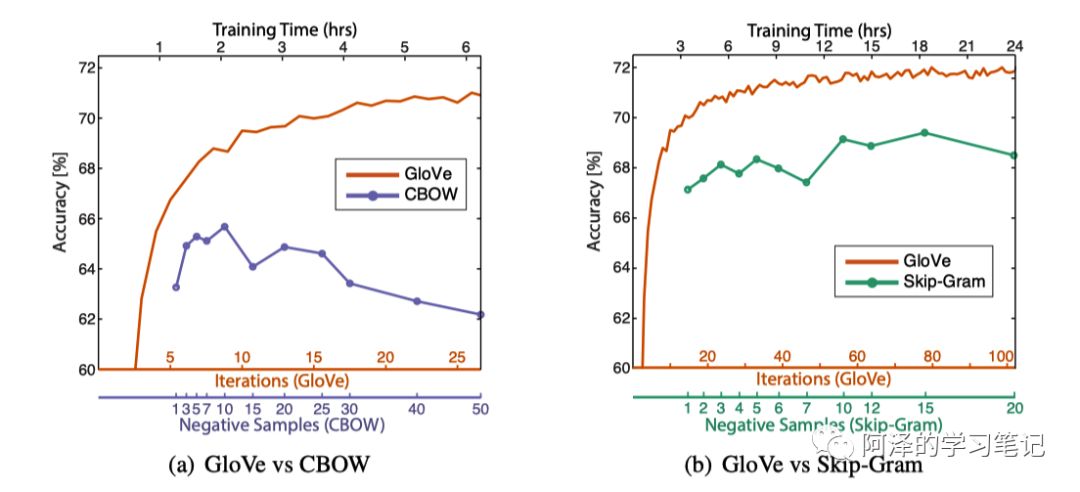
还有参数敏感性的实验：

Experiments

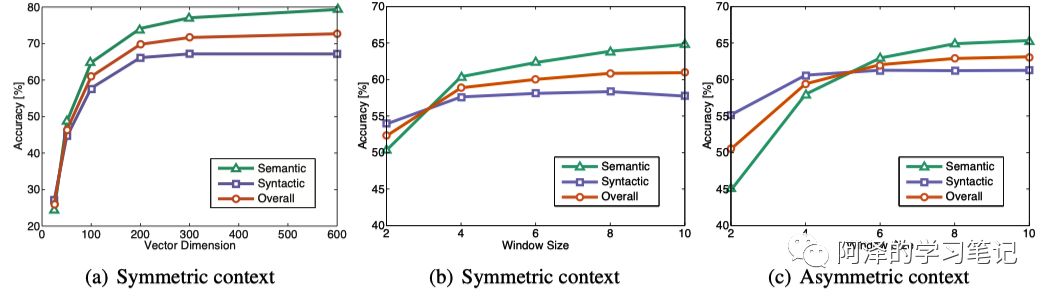
细心的同学可以看到这里有一个 Window Size 的参数，这个是用来统计共现矩阵的。

至此，我们的论文就结束了。但我看完这篇论文还有一个非常大的疑惑：GloVe 是怎么训练的呢？

4. Training

我觉得出现这个疑惑一个很大的原因在于，我一直以为 GloVe 是在 Skip-Gram 架构的基础上添加语料库的全局信息，所以也没有太明白为什么论文要证明 Word2Vec 的代价函数与 GloVe 的代价函数相似。

但其实 GloVe 与 LSA 更相关，我们来看下 GloVe 推导的公式：

是不是和带有偏置的 SVD 的数学表达式很像：

这样一看应该就明白了，GloVe 的训练方式其实和 SVD 类似。而推导 Skip-Gram  的代价函数其实是为了证明其代价函数与 GloVe 设计的代价函数是有关的。所以 Glove 更像是拥有 LSA 的优点，并加入 Skip-Gram 的优点，而不是反过来的。

下面简要给出 GloVe 的训练过程：

1. 首先，预统计 GloVe 的共现矩阵；
2. 接着，随机初始化两个矩阵：W 和   ，大小为  ，还有两个偏置向量：B 和   大小为  ；
3. 然后，计算 GloVe 的损失函数，并通过 Adagrad 来更新参数，参数包括两个矩阵和两个偏置向量；
4. 最后，重复第三步知道达到停止条件后结束训练。

我们最终得到的词向量为 W 和  ，类似于 Skip-Gram 里面的输入矩阵和输出矩阵。

那么问题来了：为什么不用一个矩阵和一个偏置项呢？这样计算量还可以减少一半，何乐不为？

欢迎大家在留言区讨论留言。

我们再简单分析一下 GloVe 的时间复杂度，从上面的实验结果来看 GloVe 的速度是非常快的，其原因主要有以下几点：

1. 时间复杂度低，最差为 O(C) ，即统计一遍语料库的共现矩阵，具体推导看论文；
2. 参数稀疏，可以用异步梯度下降算法进行优化；
3. 关注全局信息，收敛速度快。

5. Conclusion

至此，我们便结束了 GloVe 的介绍，用一句话总结便是：GloVe 使用具有全局信息的共现矩阵，并采用类似矩阵分解的方式求解词向量，通过修改代价函数将 Word2Vec 关注局部特征的优点加入进来，并取得了良好的效果。

我们尝试着将 GloVe 与 Word2Vec 进行对比：

1. Word2Vec 有神经网络，GloVe 没有；
2. Word2Vec 关注了局部信息，GloVe 关注局部信息和全局信息；
3. 都有滑动窗口但 Word2Vec 是用来训练的，GloVe 是用来统计共现矩阵的；
4. GloVe 的结构比 Word2Vec 还要简单，所以速度更快；
5. Word2Vec 是无监督学习，而 GloVe 可是视为有监督的，其 Label 为  。

再试着将 GLoVe 与 SVD 进行对比：

1. SVD 所有单词统计权重一致，GloVe 对此进行了优化；
2. GloVe 使用比值而没有直接使用共现矩阵。

当然 GloVe 看着那么好，其实并不一定，在很多任务中都没 Word2Vec 的效果好。

毕竟没有最好的模型，只有最适合的模型。

6. Reference

1. 《GloVe: Global Vectors for Word Representation》

推荐阅读

AINLP年度阅读收藏清单

斯坦福大学NLP组Python深度学习自然语言处理工具Stanza试用

DistilBERT Understanding

太赞了！Springer面向公众开放电子书籍，附65本数学、编程、机器学习、深度学习、数据挖掘、数据科学等书籍链接及打包下载

数学之美中盛赞的 Michael Collins 教授，他的NLP课程要不要收藏？

自动作诗机&藏头诗生成器：五言、七言、绝句、律诗全了

模型压缩实践系列之——bert-of-theseus，一个非常亲民的bert压缩方法

这门斯坦福大学自然语言处理经典入门课，我放到B站了

征稿启示 | 稿费+GPU算力+星球嘉宾一个都不少

关于AINLP

AINLP 是一个有趣有AI的自然语言处理社区，专注于 AI、NLP、机器学习、深度学习、推荐算法等相关技术的分享，主题包括文本摘要、智能问答、聊天机器人、机器翻译、自动生成、知识图谱、预训练模型、推荐系统、计算广告、招聘信息、求职经验分享等，欢迎关注！加技术交流群请添加AINLPer(id：ainlper)，备注工作/研究方向+加群目的。