CNN、RNN、DNN的内部网络结构有什么区别？

来源：AI量化百科

神经网络技术起源于上世纪五、六十年代，当时叫感知机（perceptron），拥有输入层、输出层和一个隐含层。输入的特征向量通过隐含层变换达到输出层，在输出层得到分类结果。早期感知机的推动者是Rosenblatt。（扯一个不相关的：由于计算技术的落后，当时感知器传输函数是用线拉动变阻器改变电阻的方法机械实现的，脑补一下科学家们扯着密密麻麻的导线的样子…）

但是，Rosenblatt的单层感知机有一个严重得不能再严重的问题，即它对稍复杂一些的函数都无能为力（比如最为典型的“异或”操作）。连异或都不能拟合，你还能指望这货有什么实际用途么o(╯□╰)o

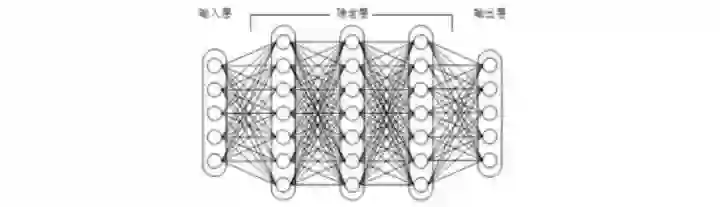
随着数学的发展，这个缺点直到上世纪八十年代才被Rumelhart、Williams、Hinton、LeCun等人（反正就是一票大牛）发明的多层感知机（multilayer perceptron）克服。多层感知机，顾名思义，就是有多个隐含层的感知机（废话……）。好好，我们看一下多层感知机的结构：

图1：上下层神经元全部相连的神经网络——多层感知机

多层感知机可以摆脱早期离散传输函数的束缚，使用sigmoid或tanh等连续函数模拟神经元对激励的响应，在训练算法上则使用Werbos发明的反向传播BP算法。对，这货就是我们现在所说的神经网络NN——神经网络听起来不知道比感知机高端到哪里去了！这再次告诉我们起一个好听的名字对于研（zhuang）究（bi）很重要！

多层感知机解决了之前无法模拟异或逻辑的缺陷，同时更多的层数也让网络更能够刻画现实世界中的复杂情形。相信年轻如Hinton当时一定是春风得意。

多层感知机给我们带来的启示是，神经网络的层数直接决定了它对现实的刻画能力——利用每层更少的神经元拟合更加复杂的函数[1]。

（Bengio如是说：functions that can be compactly represented by a depth k architecture might require an exponential number of computational elements to be represented by a depth k − 1 architecture.）

即便大牛们早就预料到神经网络需要变得更深，但是有一个梦魇总是萦绕左右。随着神经网络层数的加深，优化函数越来越容易陷入局部最优解，并且这个“陷阱”越来越偏离真正的全局最优。利用有限数据训练的深层网络，性能还不如较浅层网络。同时，另一个不可忽略的问题是随着网络层数增加，“梯度消失”现象更加严重。具体来说，我们常常使用sigmoid作为神经元的输入输出函数。对于幅度为1的信号，在BP反向传播梯度时，每传递一层，梯度衰减为原来的0.25。层数一多，梯度指数衰减后低层基本上接受不到有效的训练信号。

2006年，Hinton利用预训练方法缓解了局部最优解问题，将隐含层推动到了7层[2]，神经网络真正意义上有了“深度”，由此揭开了深度学习的热潮。这里的“深度”并没有固定的定义——在语音识别中4层网络就能够被认为是“较深的”，而在图像识别中20层以上的网络屡见不鲜。为了克服梯度消失，ReLU、maxout等传输函数代替了sigmoid，形成了如今DNN的基本形式。单从结构上来说，全连接的DNN和图1的多层感知机是没有任何区别的。

值得一提的是，今年出现的高速公路网络（highway network）和深度残差学习（deep residual learning）进一步避免了梯度消失，网络层数达到了前所未有的一百多层（深度残差学习：152层）[3,4]！具体结构题主可自行搜索了解。如果你之前在怀疑是不是有很多方法打上了“深度学习”的噱头，这个结果真是深得让人心服口服。

图2：缩减版的深度残差学习网络，仅有34层，终极版有152层，自行感受一下

如图1所示，我们看到全连接DNN的结构里下层神经元和所有上层神经元都能够形成连接，带来的潜在问题是参数数量的膨胀。假设输入的是一幅像素为1K*1K的图像，隐含层有1M个节点，光这一层就有10^12个权重需要训练，这不仅容易过拟合，而且极容易陷入局部最优。另外，图像中有固有的局部模式（比如轮廓、边界，人的眼睛、鼻子、嘴等）可以利用，显然应该将图像处理中的概念和神经网络技术相结合。此时我们可以祭出题主所说的卷积神经网络CNN。对于CNN来说，并不是所有上下层神经元都能直接相连，而是通过“卷积核”作为中介。同一个卷积核在所有图像内是共享的，图像通过卷积操作后仍然保留原先的位置关系。

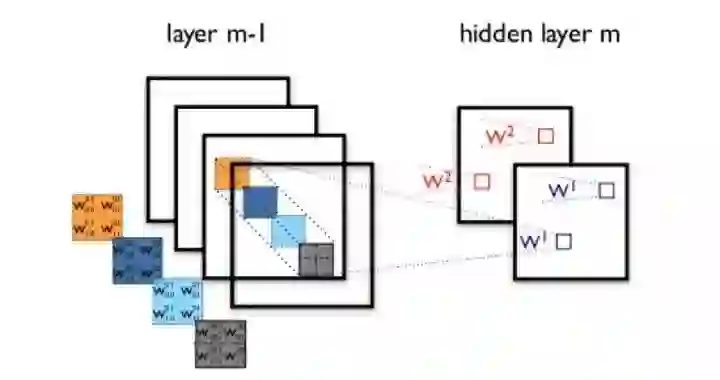
两层之间的卷积传输的示意图如下：

图3：卷积神经网络隐含层（摘自Theano教程）

通过一个例子简单说明卷积神经网络的结构。假设图3中m-1=1是输入层，我们需要识别一幅彩色图像，这幅图像具有四个通道ARGB（透明度和红绿蓝，对应了四幅相同大小的图像），假设卷积核大小为100100，共使用100个卷积核w1到w100（从直觉来看，每个卷积核应该学习到不同的结构特征）。用w1在ARGB图像上进行卷积操作，可以得到隐含层的第一幅图像；这幅隐含层图像左上角第一个像素是四幅输入图像左上角100100区域内像素的加权求和，以此类推。同理，算上其他卷积核，隐含层对应100幅“图像”。每幅图像对是对原始图像中不同特征的响应。按照这样的结构继续传递下去。CNN中还有max-pooling等操作进一步提高鲁棒性。

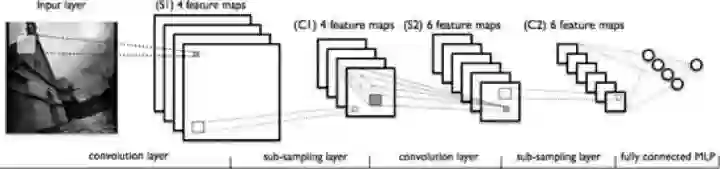
图4：一个典型的卷积神经网络结构，注意到最后一层实际上是一个全连接层（摘自Theano教程）

在这个例子里，我们注意到输入层到隐含层的参数瞬间降低到了100100100=10^6个！这使得我们能够用已有的训练数据得到良好的模型。题主所说的适用于图像识别，正是由于CNN模型限制参数了个数并挖掘了局部结构的这个特点。顺着同样的思路，利用语音语谱结构中的局部信息，CNN照样能应用在语音识别中。

全连接的DNN还存在着另一个问题——无法对时间序列上的变化进行建模。然而，样本出现的时间顺序对于自然语言处理、语音识别、手写体识别等应用非常重要。对了适应这种需求，就出现了题主所说的另一种神经网络结构——循环神经网络RNN。

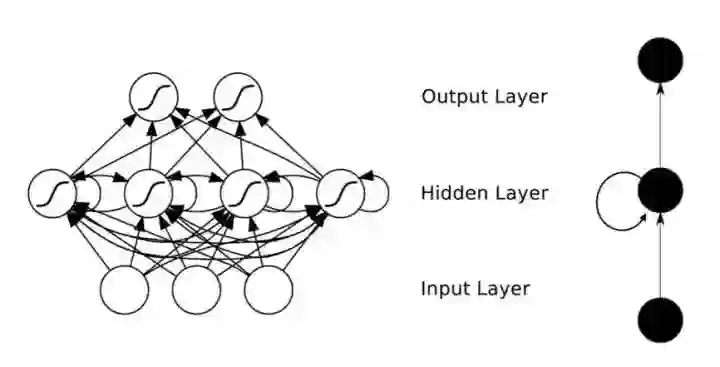
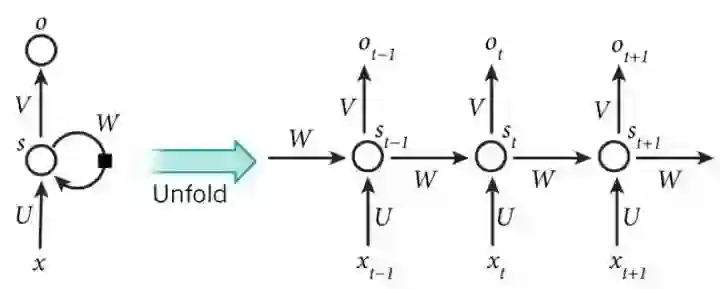
在普通的全连接网络或CNN中，每层神经元的信号只能向上一层传播，样本的处理在各个时刻独立，因此又被成为前向神经网络(Feed-forward Neural Networks)。而在**RNN中，神经元的输出可以在下一个时间戳直接作用到自身，即第i层神经元在m时刻的输入，除了（i-1）层神经元在该时刻的输出外，还包括其自身在（m-1）时刻的输出！表示成图就是这样的：

图5：RNN网络结构

我们可以看到在隐含层节点之间增加了互连。为了分析方便，我们常将RNN在时间上进行展开，得到如图6所示的结构：

图6：RNN在时间上进行展开

Cool，（t+1）时刻网络的最终结果O(t+1)是该时刻输入和所有历史共同作用的结果！这就达到了对时间序列建模的目的。

不知题主是否发现，RNN可以看成一个在时间上传递的神经网络，它的深度是时间的长度！正如我们上面所说，“梯度消失”现象又要出现了，只不过这次发生在时间轴上。对于t时刻来说，它产生的梯度在时间轴上向历史传播几层之后就消失了，根本就无法影响太遥远的过去。因此，之前说“所有历史”共同作用只是理想的情况，在实际中，这种影响也就只能维持若干个时间戳。

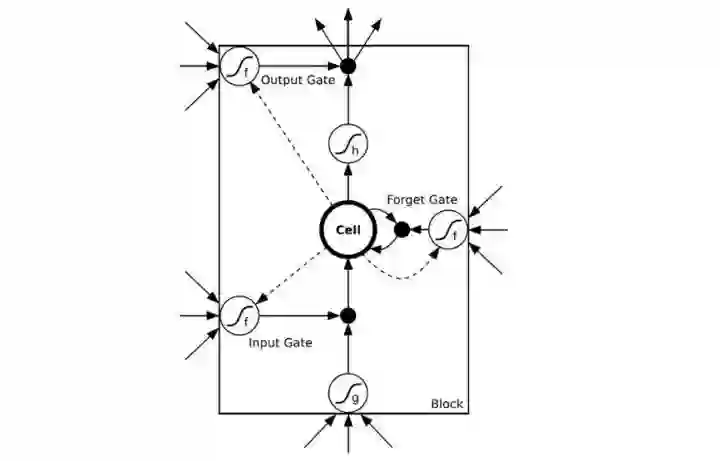
为了解决时间上的梯度消失，机器学习领域发展出了长短时记忆单元LSTM，通过门的开关实现时间上记忆功能，并防止梯度消失，一个LSTM单元长这个样子：

图7：LSTM的模样

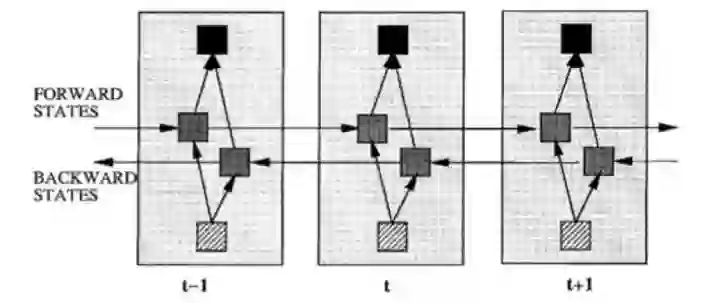
除了题主疑惑的三种网络，和我之前提到的深度残差学习、LSTM外，深度学习还有许多其他的结构。举个例子，RNN既然能继承历史信息，是不是也能吸收点未来的信息呢？因为在序列信号分析中，如果我能预知未来，对识别一定也是有所帮助的。因此就有了双向RNN、双向LSTM，同时利用历史和未来的信息。

图8：双向RNN

事实上，不论是那种网络，他们在实际应用中常常都混合着使用，比如CNN和RNN在上层输出之前往往会接上全连接层，很难说某个网络到底属于哪个类别。不难想象随着深度学习热度的延续，更灵活的组合方式、更多的网络结构将被发展出来。尽管看起来千变万化，但研究者们的出发点肯定都是为了解决特定的问题。如果想进行这方面的研究，不妨仔细分析一下这些结构各自的特点以及它们达成目标的手段。

入门的话可以参考：Ng写的Ufldl：UFLDL教程 - Ufldl

也可以看Theano内自带的教程，例子非常具体：Deep Learning Tutorials

未来智能实验室是人工智能学家与科学院相关机构联合成立的人工智能，互联网和脑科学交叉研究机构。

未来智能实验室的主要工作包括：建立AI智能系统智商评测体系，开展世界人工智能智商评测；开展互联网（城市）云脑研究计划，构建互联网（城市）云脑技术和企业图谱，为提升企业，行业与城市的智能水平服务。

  如果您对实验室的研究感兴趣，欢迎加入未来智能实验室线上平台。扫描以下二维码或点击本文左下角“阅读原文”