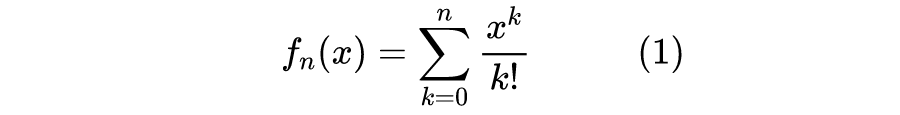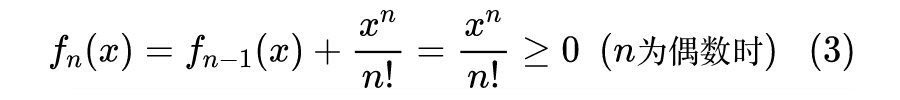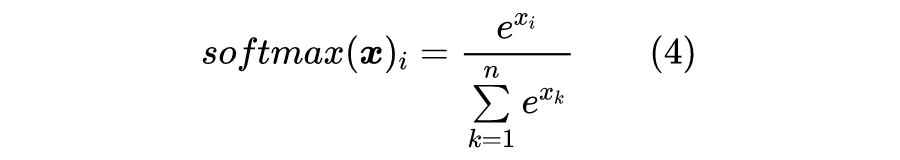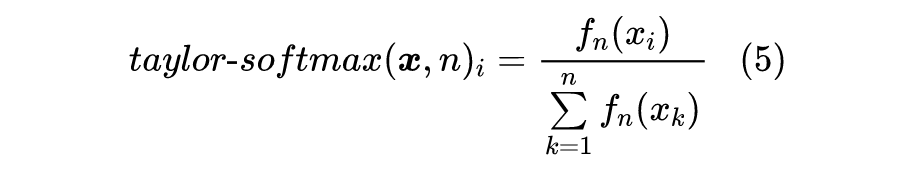探究Softmax的替代品:exp(x)的偶次泰勒展开式总是正的
证明过程
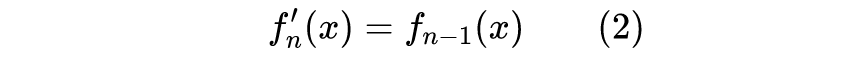
应用场景
事实上,笔者是在 Arxiv 的新文章 Exploring Alternatives to Softmax Function [1] 看到这个结论的。原论文给出了一个基于数学归纳法的比较复杂的证明,上述证明则是笔者自己构思的,相对来说更加简单明了一些。
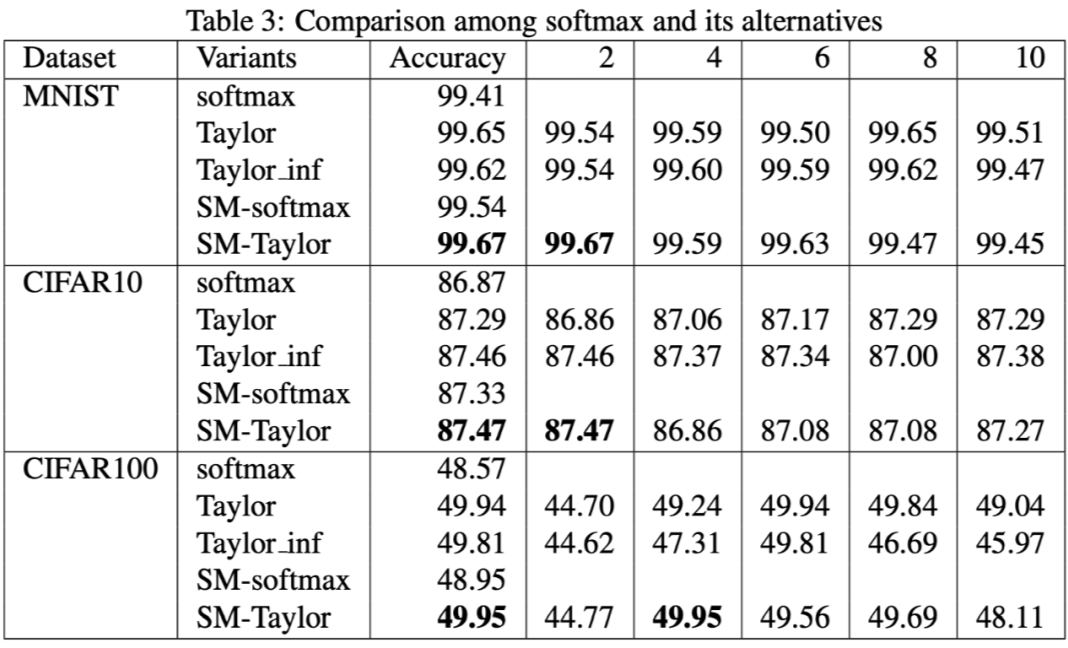
▲ softmax与其泰勒展开近似的效果比较
稍加评述
然而,在笔者看来,这个实验结果很难有什么说服力,毕竟所用的 baseline 效果太低了(都 2020 年了,你好歹跑个 ResNet 吧?)。此外,原论文也没有提供关于这个替代品的一些直观理解,纯粹是做了简单的实验然后说它 work 了,实在是过于粗糙。
文章小结
参考文献
更多阅读


#投 稿 通 道#
让你的论文被更多人看到
如何才能让更多的优质内容以更短路径到达读者群体,缩短读者寻找优质内容的成本呢?答案就是:你不认识的人。
总有一些你不认识的人,知道你想知道的东西。PaperWeekly 或许可以成为一座桥梁,促使不同背景、不同方向的学者和学术灵感相互碰撞,迸发出更多的可能性。
PaperWeekly 鼓励高校实验室或个人,在我们的平台上分享各类优质内容,可以是最新论文解读,也可以是学习心得或技术干货。我们的目的只有一个,让知识真正流动起来。
📝 来稿标准:
• 稿件确系个人原创作品,来稿需注明作者个人信息(姓名+学校/工作单位+学历/职位+研究方向)
• 如果文章并非首发,请在投稿时提醒并附上所有已发布链接
• PaperWeekly 默认每篇文章都是首发,均会添加“原创”标志
📬 投稿邮箱:
• 投稿邮箱:hr@paperweekly.site
• 所有文章配图,请单独在附件中发送
• 请留下即时联系方式(微信或手机),以便我们在编辑发布时和作者沟通
🔍
现在,在「知乎」也能找到我们了
进入知乎首页搜索「PaperWeekly」
点击「关注」订阅我们的专栏吧
关于PaperWeekly
PaperWeekly 是一个推荐、解读、讨论、报道人工智能前沿论文成果的学术平台。如果你研究或从事 AI 领域,欢迎在公众号后台点击「交流群」,小助手将把你带入 PaperWeekly 的交流群里。