HyperNTF: A Hypergraph Regularized Nonnegative Tensor Factorization for Dimensionality Reduction

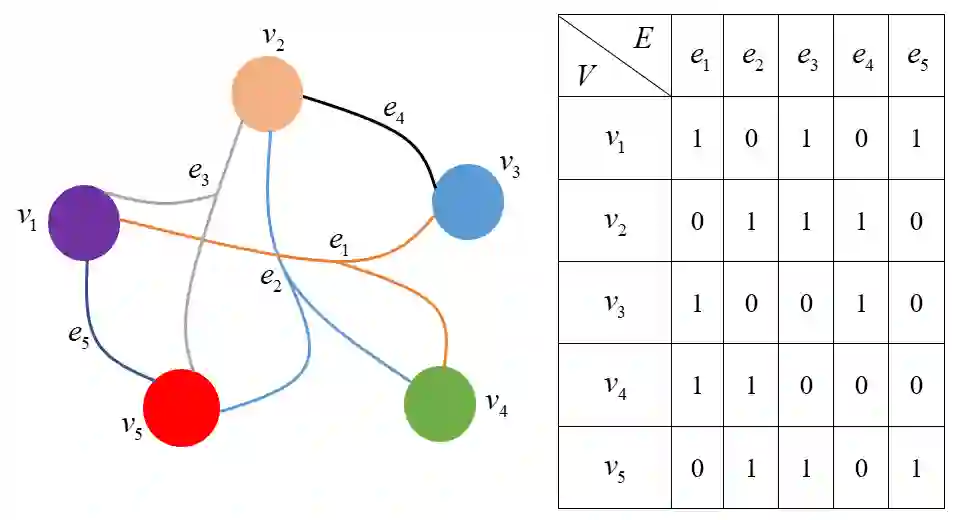
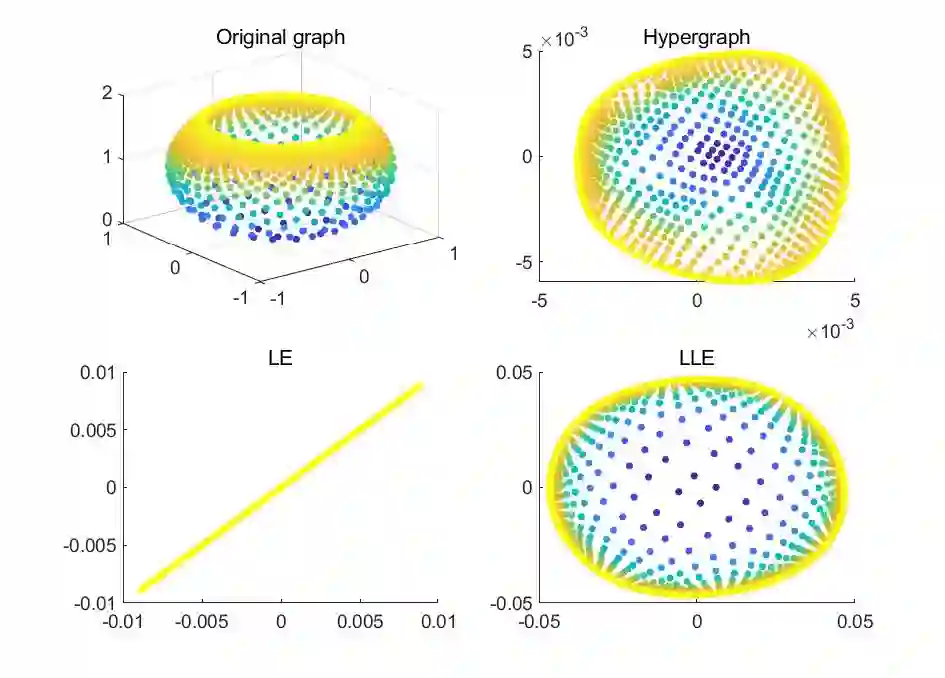
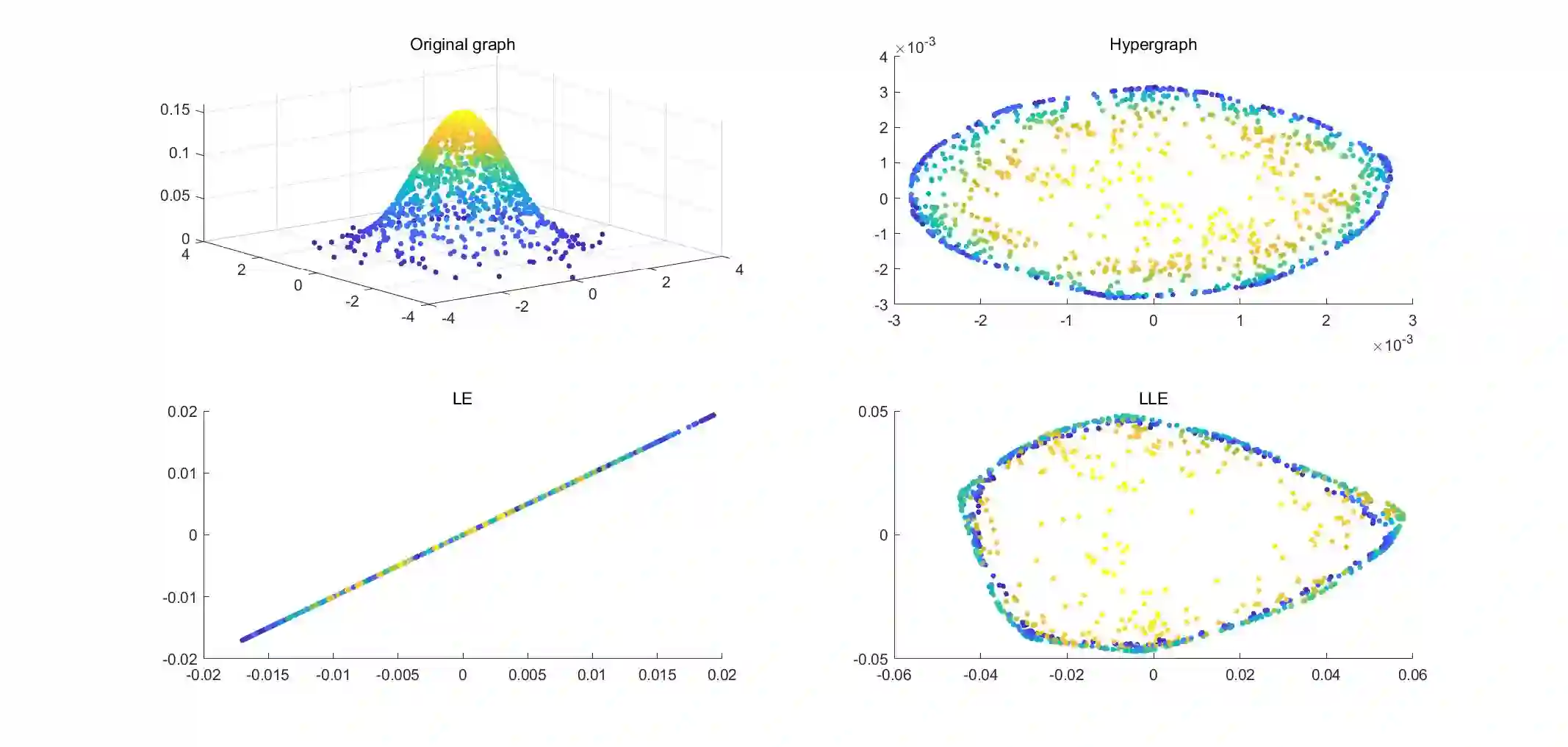
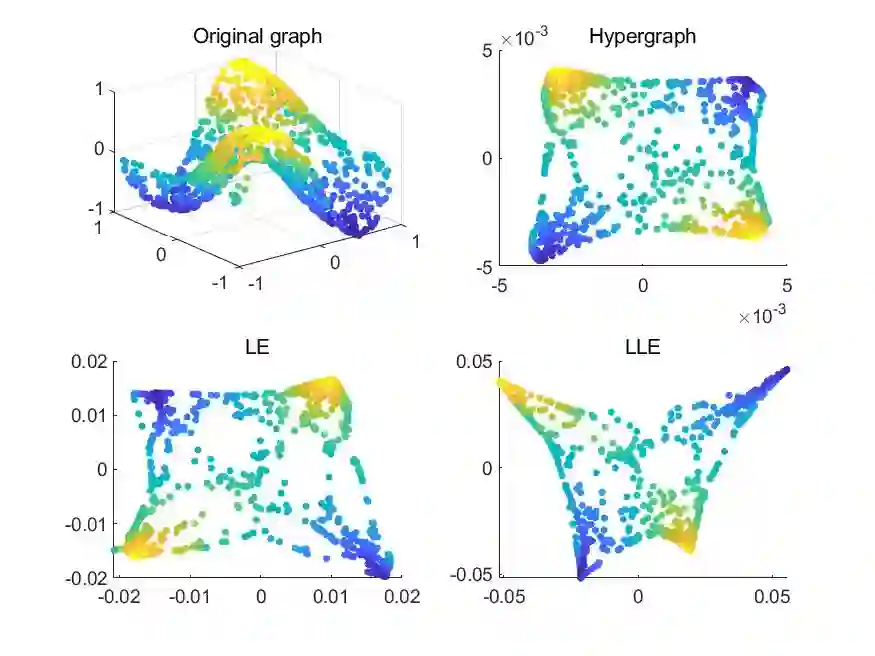
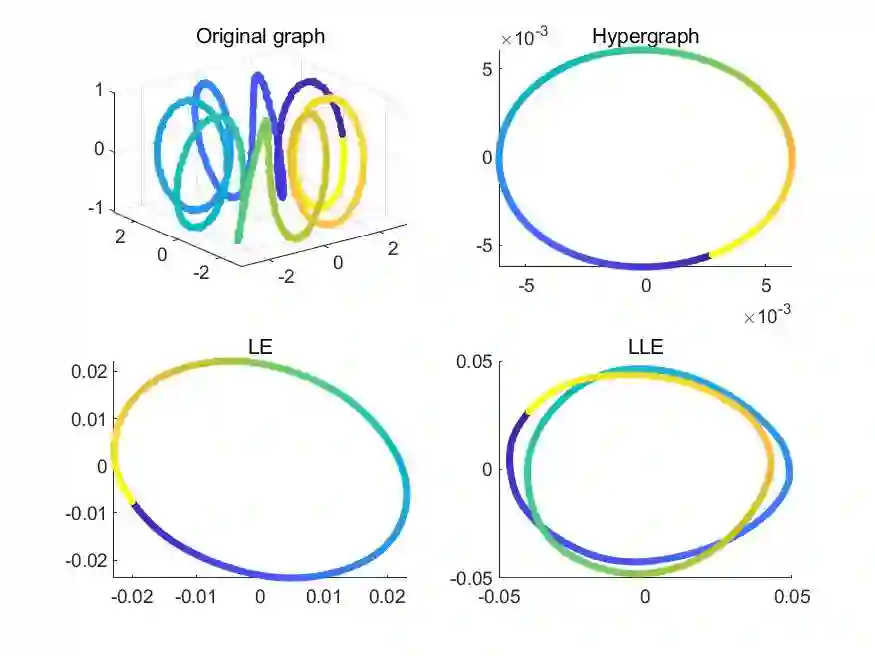
Most methods for dimensionality reduction are based on either tensor representation or local geometry learning. However, the tensor-based methods severely rely on the assumption of global and multilinear structures in high-dimensional data; and the manifold learning methods suffer from the out-of-sample problem. In this paper, bridging the tensor decomposition and manifold learning, we propose a novel method, called Hypergraph Regularized Nonnegative Tensor Factorization (HyperNTF). HyperNTF can preserve nonnegativity in tensor factorization, and uncover the higher-order relationship among the nearest neighborhoods. Clustering analysis with HyperNTF has low computation and storage costs. The experiments on four synthetic data show a desirable property of hypergraph in uncovering the high-order correlation to unfold the curved manifolds. Moreover, the numerical experiments on six real datasets suggest that HyperNTF robustly outperforms state-of-the-art algorithms in clustering analysis.