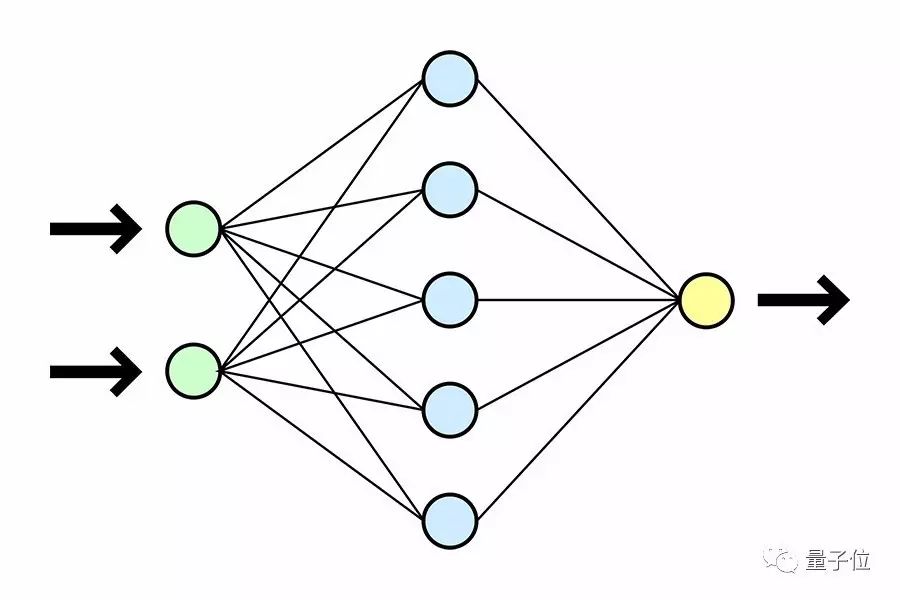
我搭的神经网络不work该怎么办！看看这11条新手最容易犯的错误

新媒体管家

声明：本文转载自公众号 量子位，由王瀚宸，王小新 翻译自博客 TheOrangeDuck

每个人在调试神经网络的时候，大概都遇到过这样一个时刻：

什么鬼！我的神经网络就是不work！到底该怎么办！

机器学习博客TheOrangeDuck的作者，育碧蒙特利尔实验室的机器学习研究员Daniel Holden，根据自己工作中失败的教训，整理了一份神经网络出错原因清单，一共11条。各位被神经网络虐待的时候，可以按图索骥。

1. 忘了数据规范化

What?

在使用神经网络的过程中，非常重要的一点是要考虑好怎样规范化（normalize）你的数据。

这一步不能马虎，不正确、仔细完成规范化的话，你的网络将会不能正常工作。

因为规范化数据这个重要的步骤在深度学习圈中早已被大家熟知，所以论文中很少提到，因此常会成为初学者的阻碍。

How?

大体上说，规范化是指从数据中减去平均值，然后再除以标准差的操作。

通常这个操作对每个输入和输出特征是分别完成的，但你可能会想同时对一整组的特征进行规范化，再挑出其中一些特殊处理。

Why?

我们需要规范化数据的主要原因是，在神经网络中几乎所有的数据传输途径中，都是假设输入和输出的数据结构满足标准差接近于1，平均值几乎为0。这个假设在深度学习中的每个地方都会出现，从权重因子的初始化，到活化函数，再到训练网络的优化算法。

And?

一个未训练的神经网络通常输出的结果范围从-1到1。如果你希望它的输出值在其它的范围，比如说RGB图片表示颜色的值域就是0到255，你将会遇到麻烦。

当期望的输出值是255，神经网络开始训练时情况会极不稳定，因为实际产生的值为-1或者1，对大多数用来训练神经网络的优化算法来说，这和255相比都有巨大的误差。这将会产生巨大的梯度，你的训练误差很可能会爆表。

就算碰巧在你训练的起始阶段，误差没有爆表，这个过程仍然是没有意义的，因为神经网络在向错误的方向学习和发展。

如果你先将你的数据规范化（在这个例子中你可以将RGB值除以128然后减去1），那么这些情况就都不会发生。

总体来说，神经网络中各种特征的值域决定了他们的重要性。

如果输出中的一项特征的值域很大，那么意味着与其他特征相比，它将会产生更大的误差。同样地，输入中值域大的特征也会支配着网络，在下游中引起更大的变化。

因此，仅仅依靠许多神经网络库中的自动规范化，盲目地减去平均值后再除以方差，并不总是合适的做法。可能有这样一个输入特征，取值范围通常在0到0.001之间，它的值域这么小是因为这个特征不重要，还是因为它与其他特征相比有着更小的单位呢？这决定了你要不要将它规范化。

类似地，还要谨慎对待那些值域较小的特征，因为它们的标准差可能很小，接近或者严格等于0。如果你对它们进行规范化，可能会产生NaN(Not a Number)的错误。

这种情况需要谨慎地对待，要仔细琢磨你的这些特征真正代表着什么，以及考虑规范化的过程是为了将所有输入的特征等价。

这是少数几个我认为在深度学习中需要人类完成的任务。

2. 没有检查结果

What?

当你训练网络经过了几个epoch之后，误差（error）开始下降了——成功！

但这是否意味着你完成了训练呢？博士能毕业了吗？很不幸，答案是否定的。

你的代码中，基本上还肯定还存在一些错误。这个bug可能存在于数据预处理，训练网络甚至是最后给出推断结果的过程中。

只是误差开始下降，并不意味着你的网络学到了“真功夫”。

How?

毋庸置疑，在数据传输过程中的每个阶段检查数据正确性都很重要，通常这意味着要通过一些方法来对结果进行可视化。

如果你的数据是图像，那么情况就很简单，相应的动画数据很好生成。但如果你的数据比较奇葩，也要找出一种合适的方法，能够在预处理、网络训练和数据传递的每个阶段来检查数据的正确性，将其与原始的真实数据比较。

Why?

跟传统的编程过程不同，机器学习系统失败时都不出声。

在传统编程中，我们习惯了当遭遇状况时计算机报错，随后我们可以结合报错内容来debug。不幸的是，这个过程并不适用于机器学习应用。

所以，我们需要极其小心地在每个阶段检查我们的过程是否有问题，从而能够察觉到bug的产生，以及在需要回头仔细检查代码的时候及时发现。

And?

有许多种方法来检查你的网络是否有效。其中之一是要明确训练误差的意义。将在训练集上运行的神经网络的输出结果进行可视化——输出结果跟实际情况相比怎样？

你可能看到在训练过程中误差从100下降到1，但最终结果仍然是不可用的，因为在实际场景中误差为1仍然是不可接受的结果。如果网络在训练集上有效，那么再在验证集上测试——它是否同样适用于之前没有见过的数据呢？

我的建议是从一开始就可视化所有过程，不要等网络不奏效时再开始做，在你开始尝试不同的神经网络结构之前，你要确保整个流程没有一丝差错。这是你能够正确评估不同网络模型的唯一方式。

3. 忘了数据预处理

What？

绝大部分数据都很tricky。我们认为非常相似的事物，从数据上看可能拥有完全不同的数值表达形式。

就拿视频中的人物动作来说，如果我们数据是在一个特定地点或是特点方向上，记录人物的关节相对于录像中心的3D位置，那么换一个方向或地点，可能同一套动作会拥有完全不同的数字表达形式。

因此，我们需要用新的方式来表达我们的数据，比如说放到一些本地参考系中（诸如跟人物的质心相关的一些），让相似的动作有相似的数值表达。

How？

思考你的特征具体代表着什么——你是否可以在它们上面做一些简单的变换，来确保用来代表相似事物的数据点通常具有相似的数值表达？是否存在一个本地坐标系，能以一种不同的形式更自然地表达你的数据？比如说一个更好的色彩空间？

Why？

神经网络只对输入的数据做一些最基本的假设，但是这些假设中有一条，是认为这些数据分布的空间是连续的，即对于空间中的大部分，两个数据点间的点类似这两个数据点的“混合”，相邻的数据点在某种意义上代表着相似的事情。

当数据空间中存在较大的不连续时，亦或者一大组分开的数据均代表着同一件事情时，将会使得学习任务的难度大大增加。

And？

理解数据预处理（preprocess）的另一种方式，是把它作为减少由排列组合导致的数据激增的一种尝试。

举例来说，如果一个基于人物动作训练过的神经网络需要学习在该人物在各个地点、各个方向上的同一组动作，那么将会耗费大量的资源，学习的过程将会是冗余的。

4. 忘了正则化

What?

正则化（regularization）方式是训练神经网络时另一个不可或缺的方面，通常以Dropout层、小噪声或某种形式的随机过程等方式应用到网络中。

即使在你看来当前数据规模远大于参数规模，或是在某些情况下，不会出现过拟合效应，或者就算出现也不影响效果，你仍然应该加入Dropout层或一些其他形式的小噪声。

How?

向神经网络添加正则化的一种最基本方法，是在网络中的每个线性层（如卷积层或稠密层）前加入Dropout层。

在开始设置Dropout值时，可定义中等值到较低值，如0.25或0.1。你可根据网络的各项指标，来判断过拟合程度并进行调整，若仍觉得不可能出现过拟合效应，可以将Dropout值设置到非常小，如0.01。

Why?

正则化方式不仅仅是用来控制过拟合效应，它在训练过程中引入了一些随机过程，在某种意义上“平滑”了代价格局。这种方式可加快训练进程，有助于处理数据中的异常值，并防止网络中出现极端权重结构。

And?

跟Dropout层一样，数据增强或者其他类型的噪声也可作为正则化方式。

虽然Dropout层通常被认为是一种将许多随机子网络的预测结果结合起来的技巧，但它也可看作是一种通过在训练时产生多种输入数据的相似变体来动态扩展训练集大小的方法。

而且要知道，防止过拟合并提高网络准确性的最佳方法是向神经网络输入大量且不重复的训练数据。

5. 设置了过大的批次大小

What?

设置了过大的批次（batch）大小，可能会对训练时网络的准确性产生负面影响，因为它降低了梯度下降的随机性。

How?

要在可接受的训练时间内，确定最小的批次大小。一个能合理利用GPU并行性能的批次大小可能不会达到最佳的准确率，因为在有些时候，较大的批次大小可能需要训练更多迭代周期才能达到相同的正确率。

在开始时，要大胆地尝试很小的批次大小，如16、8，甚至是1。

Why?

较小的批次大小能带来有更多起伏、更随机的权重更新。这有两个积极的作用，一是能帮助训练“跳出”之前可能卡住它的局部最小值，二是能让训练在“平坦”的最小值结束，着通常会带来更好的泛化性能。

And?

数据中其他的一些要素有时也能起到批次大小的作用。

例如，以两倍大小的先前分辨率来处理图像，得到的效果与用四倍批次大小相似。

做个直观的解释，考虑在CNN网络中，每个滤波器的权重更新值将根据输入图像的所有像素点和批次中的每张图像来进行平均，将图像分辨率提高两倍，会产生一种四倍像素量同样的平均效果，与将批次大小提高四倍的做法相似。

总体来说，最重要的是要考虑到，在每次迭代中有多少决定性的梯度更新值被平均，并确保平衡好这种不利影响与充分利用GPU并行性能的需求之间的关系。

6. 使用了不适当的学习率

What?

学习率对网络的训练效果有着巨大的影响。如果你刚入门，使用了常用深度学习框架中给出的各种默认参数，那几乎可以肯定，你的设置不对。

How?

关闭梯度裁剪，找出学习率的最大值，也就是在训练过程中不会让误差爆表的上限值。把学习率设置为比这小一点的值，很可能就非常接近最佳学习率了。

Why?

大多数深度学习框架会默认启用梯度裁剪方式。这种方式通过限制在每个步骤中可以调整权重的数量，来防止训练过程中优化策略出现崩溃。

当你的数据中包含许多异常值，会造成大幅度的梯度和权重更新，这种限制特别有用。但是在默认情况下，这种方式也会使用户很难手动找到最佳学习率。

我发现，大多数深度学习新手会设置过高的学习率，并且通过梯度裁剪来缓解此问题，使得全局训练过程变慢，并且改变学习率后的网络效果不可预测。

And?

如果你好好清洗了数据，删除了大多数异常值，并设置了合理的学习率，实际上并不需要梯度裁剪方式。如果关闭了梯度裁剪之后里，你发现网络偶尔会发生训练错误，那就再打开它。

但是要记住，发生训练错误通常表明你的数据还存在一些问题，梯度裁剪只是一个暂时的解决方法。

7. 在最后一层使用了错误的激活函数

What?

在最后一层中，不合理的激活函数有时会导致你的网络无法输出所需值的全部范围。最常见的错误是，在最后一层使用ReLU函数，导致网络只能产生正值输出。

How?

如果要实现回归任务，那么在最后一层通常不需要使用任何激活函数，除非你详细地知道你想输出哪一类值。

Why?

再次确认下你输入数据的实际意义，以及归一化后的具体范围。

很可能出现的情况是，网络的输出区间是从负无穷大到正无穷大，在这种情况下，你不该在最后一层使用激活函数。

如果网络输出只在某个区间内有意义，则需使用一些特殊的激活函数。比如，某网络输出为[0, 1]区间的概率值，根据这种情况可使用S形激活函数。

And?

在选择最后一层的激活函数时，有许多玄学。

在神经网络产生输出后，你也许会将其裁剪到[-1, 1]的区间。那将这个裁剪过程当作最后一层的激活函数，这似乎是有意义的，因为这将确保网络中的误差函数不会对不在[-1, 1]区间外的值进行惩罚。但是没有误差意味着区间外的这些值没有对应梯度，这在某些情况下无法进行网络训练。

或者，你也可以在最后一层使用tanh函数，因为这个激活函数的输出范围是[-1, 1]。但是这也可能出现问题，因为这个函数在1或-1附近时斜率变得很大，可能会使权重大幅增加，最终只产生-1或1的输出。

一般来说，最好的选择通常是采用求稳策略，在最后一层不使用任何激活函数，而不是试图使用一些机灵的技巧，可能会适得其反。

8. 网络含有不良梯度

What?

使用ReLU激活函数的深度神经网络通常可能遭受由不良梯度引起的所谓“死神经元”。这可能会对网络的性能产生负面影响，或者在某些情况下导致完全无法训练。

How?

如果发现在epoch到epoch之间，你的训练误差不会变化，就可能是由于ReLU激活函数导致了所有的神经元已经死亡。

换一个激活函数试试，比如leaky ReLU或ELU，看看是不是还会发生同样的情况。

Why?

ReLU激活函数的梯度对于正值为1，对于负值为0。这是因为对于小于0的输入来说，输入的很小变化不会影响输出。

这可能看起来不是一个问题，因为正值的梯度很大。但是很多层叠在一起，而负权重可以将具有强梯度的大正值变为0梯度的负值。

你可能经常发现，无论输入什么，部分甚至全部隐藏单元对成本函数都是0梯度，这就是所谓的网络“已死”，所有权重都无法更新。

And?

很多运算都具有0梯度，比如裁剪，舍入，或取最大/最小值，如果用它们来计算成本函数相对于权重的导数，都会产生不良梯度。

如果它们出现在你的符号图的任何地方，要非常小心，因为它们常常会导致意想不到的困难。

9. 没有正确地初始化网络权重

What?

如果你没有正确地初始化神经网络权重，那么神经网络很可能根本就无法训练。

神经网络中有许多其他组件，会假设你的权重初始化是正确的，或者标准的，它们会将权重设置为0，或者使用你自定义的随机初始化权重，于是将不会起作用。

How?

“he”、“lecun”或“xavier”权重初始化都是受欢迎的选择，在几乎任何情况下都应该很好地工作。只要选一个（我最喜欢的是“lecun”）就行了。

但是一旦神经网络开始训练了，你就可以自由的实验，寻找最适合你任务的权重了。

Why?

你可能听说过，可以使用“小随机数”初始化神经网络权重，但并不那么简单。

所有上述初始化方法都是靠复杂、细致的数学发现的，这也说明了为什么它们是最佳的。

更重要的是，很多其他神经网络组件都是围绕这些初始化构建的，并根据经验使用它们进行测试 ，自己进行初始化可能会导致难以复现其他研究者的成果。

And?

其他层可能也需要仔细地初始化。网络偏移被初始化为零，而其他更复杂的层（如参数激活函数）可能会带有自己的初始化，这与正确的同样重要。

10. 神经网络太深了

What?

网络越深越好？不一定。

当你对网络进行基准测试，试着在一些任务上提高1%的准确度时，更深的网络通常会表现得更好。

但是如果你设计的浅层（3到5层）网络没有学习任何特征，那么可以保证，你设计的超深（如100层）网络也会没有效果，甚至更加糟糕。

How?

刚开始时，先试试浅层神经网络的效果，通常是3到8层。只有当你的网络有一定效果，要开始着手提高准确率时，再去研究更深层网络的结构。

Why?

看起来似乎是当有人决定堆一个几百层的神经网络时，神经网络模型忽然得到了突破性的结果，但事实并非如此。

在过去十年中，神经网络中所有改良技术所取得的微小进步，对浅层和深层网络都同样适用。如果你的网络不起作用，这很可能不是深度问题，是其他方面出错了。

And?

从小型网络开始训练，也意味着能更快地训练网络、更快地完成模型推理及更快地完成不同结构和参数配置的迭代过程。首先，与仅堆叠更多网络层相比，上面提到的所有方面将对模型准确率产生更大的影响。

11. 隐藏unit的数量不对

What?

某些情况下，隐藏单元太多或者太少，都会导致网络难以训练。

隐藏单元太少，可能会没有能力表达所需的任务；太多单元又会导致网络缓慢、难以训练，残留噪声难以消除。

How?

开始时的隐藏单元数量，最好在256到1024个之间。

然后，看一下研究类似应用的研究人员使用了多少个隐藏单元，找找灵感。如果你的同行所用的数量和上面给出的数字相差很远，可能会有一些特殊的原因，这可能对你来说很重要。

Why?

当决定隐藏单元的数量时，关键在于考虑要表达你想通过网络传递的信息，所需的最小真实值是多少。

然后，考虑到dropout、网络使用冗余的表示、以及为你的估计留一点余地，可以将这个数字放大一点。

如果你正在做分类，可以使用类别数目的5到10倍，作为隐藏单元的数量；如果做回归，可以使用输入或输出变量数目的2到3倍。

当然，所有这些都高度依赖于环境，没有简单的自动解决方案，决定隐藏单元数量时，最重要的依然是直觉。

And?

实际上，与其他因素相比，隐藏单元的数量通常对神经网络性能影响很小，而在许多情况下，高估所需隐藏单位的数量除了拖慢训练速度之外，也不会有什么负面影响。

一旦网络开始正常工作，如果你还是担心，可以尝试各种不同数量的隐藏单元，并测量网络精度，直到找到最合适的设置。

本期责任编辑： 郭江

本期编辑：  蔡碧波

---

“哈工大SCIR”公众号

主编：车万翔

副主编： 张伟男，丁效

责任编辑： 张伟男，丁效，郭江，赵森栋

编辑： 李家琦，赵得志，赵怀鹏，吴洋，刘元兴，蔡碧波

长按下图并点击 “识别图中二维码”，即可关注哈尔滨工业大学社会计算与信息检索研究中心微信公共号：”哈工大SCIR” 。