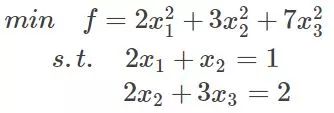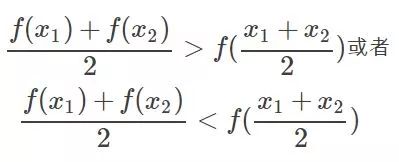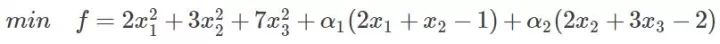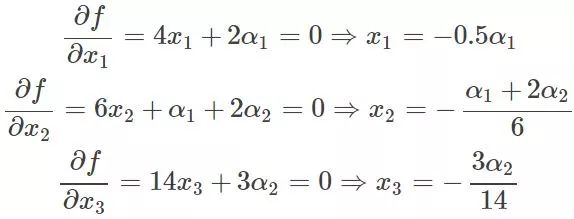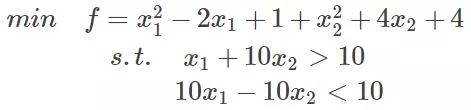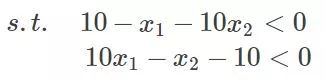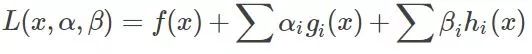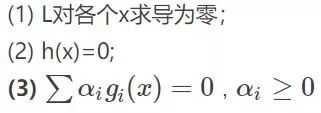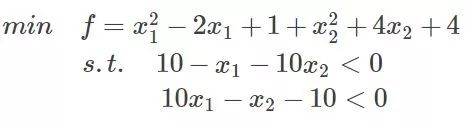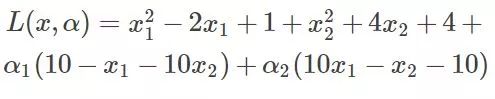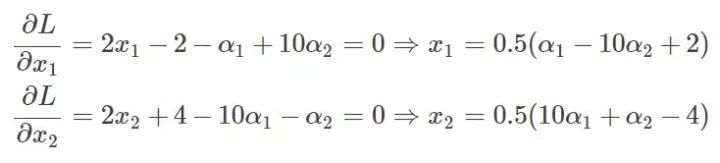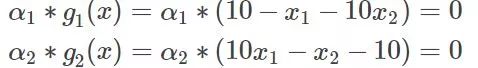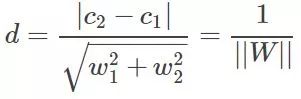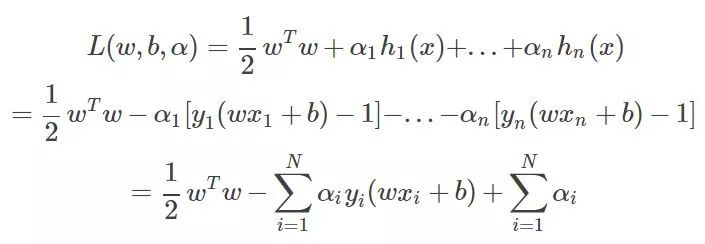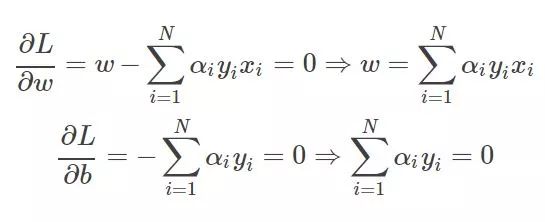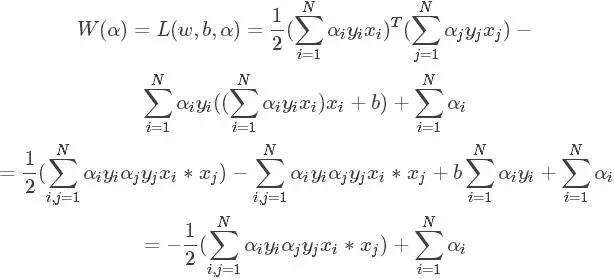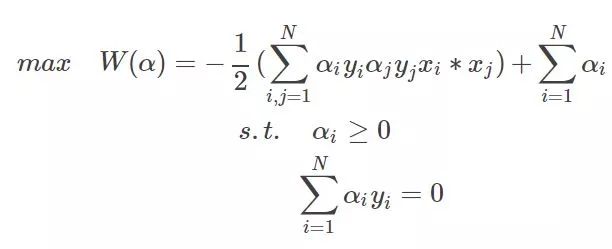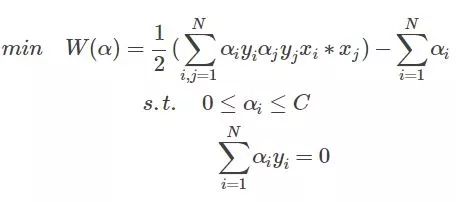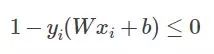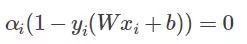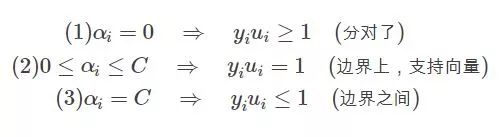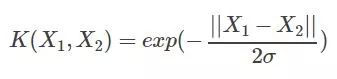SVM大解密(附代码和公式)
源 | 我i智能
支持向量机(SVM),一个神秘而众知的名字,在其出来就受到了莫大的追捧,号称最优秀的分类算法之一,以其简单的理论构造了复杂的算法,又以其简单的用法实现了复杂的问题,不得不说确实完美。
本系列旨在以基础化的过程,实例化的形式一探SVM的究竟。曾经也只用过集成化的SVM软件包,效果确实好。因为众人皆说原理复杂就对其原理却没怎么研究,最近经过一段时间的研究感觉其原理还是可以理解,这里希望以一个从懵懂到略微熟知的角度记录一下学习的过程。其实网络上讲SVM算法的多不胜数,博客中也有许多大师级博主的文章,写的也很简单明了,可是在看过之和总是感觉像差点什么,当然对于那些基础好的可能一看就懂了,然而对于像我们这些薄基础的一遍下来也能马马虎虎懂,过一两天后又忘了公式怎么来的了。比如说在研究SVM之前,你是否听说过拉格朗日乘子法?你是否知道什么是对偶问题?你是否了解它们是怎么解决问题的?Ok这些不知道的话,更别说什么是KKT条件了,哈哈,有没有说到你的心声,不用怕,学学就会了。话说像拉格朗日乘子法,在大学里面学数学的话,不应该没学过,然你学会了吗?你知道是干什么的吗?如果那个时候就会了,那你潜质相当高了。作为一个过来的人,将以简单实例化形式记录自己的学习过程,力图帮助新手级学习者少走弯路。
一、关于拉格朗日乘子法和KKT条件
1)关于拉格朗日乘子法
首先来了解拉格朗日乘子法,那么为什么需要拉格朗日乘子法?记住,有拉格朗日乘子法的地方,必然是一个组合优化问题。那么带约束的优化问题很好说,就比如说下面这个:
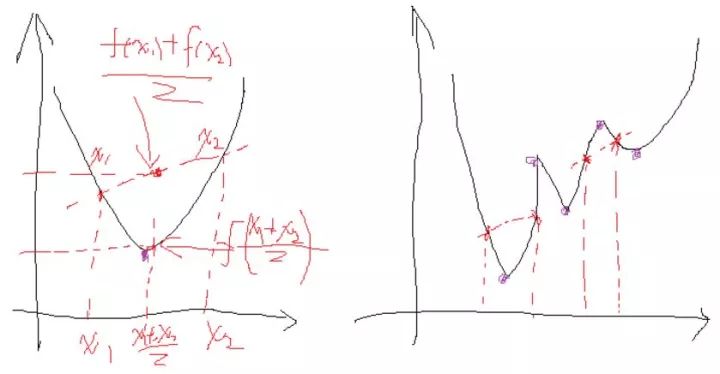
这是一个带等式约束的优化问题,有目标值,有约束条件。那么想想假设没有约束条件这个问题是怎么求解的呢?是不是直接f对各个x求导等于0,,解x就可以了,可以看到没有约束的话,求导为0,那么各个x均为0吧,这样f=0了,最小。但是x都为0不满足约束条件呀,那么问题就来了。这里在说一点的是,为什么上面说求导为0就可以呢?理论上多数问题是可以的,但是有的问题不可以。如果求导为0一定可以的话,那么f一定是个凸优化问题,什么是凸的呢?像下面这个左图:
凸的就是开口朝一个方向(向上或向下)。更准确的数学关系就是:
注意的是这个条件是对函数的任意x取值。如果满足第一个就是开口向上的凸,第二个是开口向下的凸。可以看到对于凸问题,你去求导的话,是不是只有一个极点,那么他就是最优点,很合理。类似的看看上图右边这个图,很明显这个条件对任意的x取值不满足,有时满足第一个关系,有时满足第二个关系,对应上面的两处取法就是,所以这种问题就不行,再看看你去对它求导,会得到好几个极点。然而从图上可以看到,只有其中一个极点是最优解,其他的是局部最优解,那么当真实问题的时候你选择那个?说了半天要说啥呢,就是拉格朗日法是一定适合于凸问题的,不一定适合于其他问题,还好我们最终的问题是凸问题。
回头再来看看有约束的问题,既然有了约束不能直接求导,那么如果把约束去掉不就可以了吗?怎么去掉呢?这才需要拉格朗日方法。既然是等式约束,那么我们把这个约束乘一个系数加到目标函数中去,这样就相当于既考虑了原目标函数,也考虑了约束条件,比如上面那个函数,加进去就变为:
这里可以看到与相乘的部分都为0,所以的取值为全体实数。现在这个优化目标函数就没有约束条件了吧,既然如此,求法就简单了,分别对x求导等于0,如下:
把它在带到约束条件中去,可以看到,2个变量两个等式,可以求解,最终可以得到,这样再带回去求x就可以了。那么一个带等式约束的优化问题就通过拉格朗日乘子法完美的解决了。那么更高一层的,带有不等式的约束问题怎么办?那么就需要用更一般化的拉格朗日乘子法即KKT条件来解决这种问题了。
2)关于KKT条件
继续讨论关于带等式以及不等式的约束条件的凸函数优化。任何原始问题约束条件无非最多3种,等式约束,大于号约束,小于号约束,而这三种最终通过将约束方程化简化为两类:约束方程等于0和约束方程小于0。再举个简单的方程为例,假设原始约束条件为下列所示:
那么把约束条件变个样子:
为什么都变成等号与小于号,方便后面的,反正式子的关系没有发生任何变化就行了。
现在将约束拿到目标函数中去就变成:
那么KKT条件的定理是什么呢?就是如果一个优化问题在转变完后变成
其中g是不等式约束,h是等式约束(像上面那个只有不等式约束,也可能有等式约束)。那么KKT条件就是函数的最优值必定满足下面条件:
这三个式子前两个好理解,重点是第三个式子不好理解,因为我们知道在约束条件变完后,所有的g(x)<=0,且,然后求和还要为0,无非就是告诉你,要么某个不等式,要么其对应的。那么为什么KKT的条件是这样的呢?
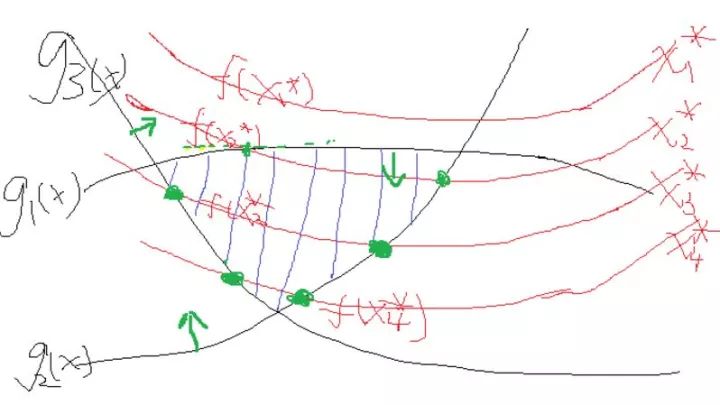
假设有一个目标函数,以及它的约束条件,形象的画出来就如下:
假设就这么几个吧,最终约束是把自变量约束在一定范围,而函数是在这个范围内寻找最优解。函数开始也不知道该取哪一个值是吧,那就随便取一个,假设某一次取得自变量集合为x1,发现一看,不满足约束,然后再换呀换,换到了x2,发现可以了,但是这个时候函数值不是最优的,并且x2使得g1(x)与g2(x)等于0了,而g3(x)还是小于0。
这个时候,我们发现在x2的基础上再寻找一组更优解要靠谁呢?当然是要靠约束条件g1(x)与g2(x),因为他们等于0了,很极限呀,一不小心,走错了就不满足它们两了,这个时候我们会选择g1(x)与g2(x)的梯度方向往下走,这样才能最大程度的拜托g1(x)与g2(x)=0的命运,使得他们满足小于0的约束条件对不对。至于这个时候需不需要管g3(x)呢?正常来说管不管都可以,如果管了,也取g3在x2处的梯度的话,因为g3已经满足了小于0的条件,这个时候在取在x2处的梯度,你能保证它是往好的变了还是往差的变了?答案是都有可能。运气好,往好的变了,可以更快得到结果,运气不好,往差的变了,反而适得其反。
那么如果不管呢?因为g1(x)与g2(x)已经在边缘了,所以取它的梯度是一定会让目标函数变好的。综合来看,这个时候我们就不选g3。那么再往下走,假设到了自变量优化到了x3,这个时候发现g2(x)与g3(x)等于0,也就是走到边了,而g1(x)小于0,可变化的空间绰绰有余,那么这个时候举要取g2(x)与g3(x)的梯度方向作为变化的方向,而不用管g1(x)。那么一直这样走呀走,最终找到最优解。可以看到的是,上述如果g1(x)、g2(x)=0的话,我们是需要优化它的,又因为他们本身的条件是小于0的,所以最终的公式推导上表明,是要乘以一个正系数作为他们梯度增长的倍数,而那些不需要管的g(x)为了统一表示,这个时候可以将这个系数设置为0,那么这一项在这一次的优化中就没有了。那么把这两种综合起来就可以表示为
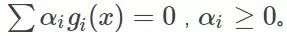
也即是某次的g(x)在为最优解起作用,那么它的系数值(可以)不为0。如果某次g(x)没有为下一次的最优解x的获得起到作用,那么它的系数就必须为0,这就是这个公式的含义。
比如上面例子的目标值与约束:
将约束提到函数中有:
此时分别对x1、x2求导数:
而我们还有一个条件就是,那么也就是:
这样我们就去讨论下,要么g=0,要么,这里两个g两个,这样我们就需要讨论四种情况,可能你会说,这是约束条件少的情况,那么如果有10个约束条件,这样就有10个g和10个,你去给我讨论?多少种组合,不知道,但是换个思路,我们非得去10个一起去讨论?机智的学者想到一种方法,考虑到这个条件,那么我两个两个讨论不就可以了,比如现在我就讨论7,8,让其他的不变,为什么选或者至少选两个讨论呢,因为这个式子求和为0,改变一个显然是不行的,那就改变两个,你增我就减,这样和可以为0。再问为什么不讨论3个呢?也可以,这不是麻烦嘛,一个俗语怎么说来着,三个和尚没水喝,假设你改变了一个,另外两个你说谁去减或者加使得和为0,还是两个都变化一点呢?不好说吧,自然界都是成双成对的才和谐,没有成三成四的(有的话也少)。
这里顺便提一下后面会介绍到的内容,就是实现SVM算法的SMO方法,在哪里,会有很多,那么人们怎么解决的呢,就是随便选择两个去变化,看看结果好的话,就接受,不好的话就舍弃在选择两个,如此反复,后面介绍。
可以看到像这种简单的讨论完以后就可以得到解了。
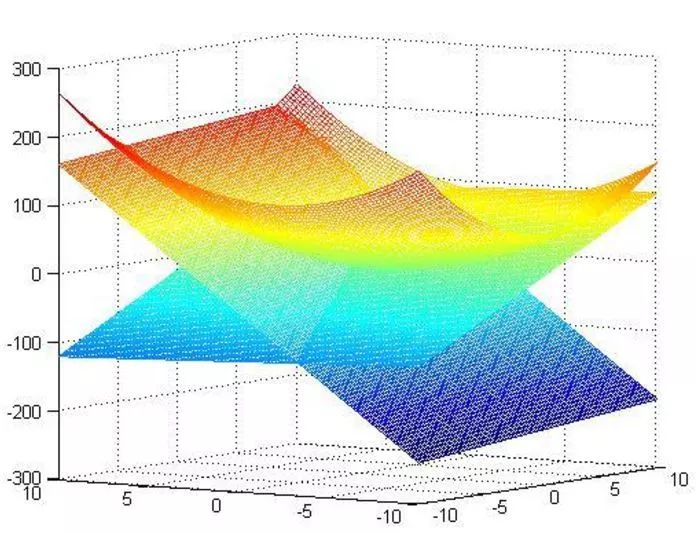
x1=110/101=1.08;x2=90/101=0.89,那么它得到结果对不对呢?这里因为函数简单,可以在matlab下画出来,同时约束条件也可以画出来,那么原问题以及它的约束面画出来就如下所示:
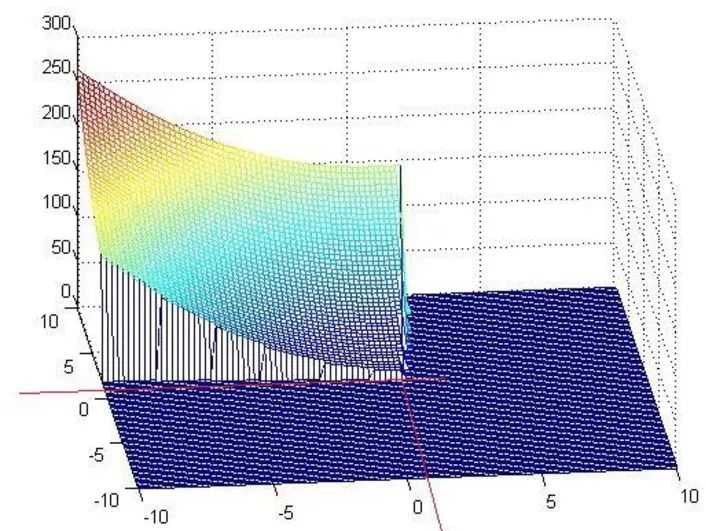
这是截取下来的符合约束要求的目标面
可以看到最优解确实就是上面我们求的那个解。既然简单的问题可以这样解,那么复杂一点的只需要简单化,照样可以解,至此KKT条件解这类约束性问题就是这样,它对后续的SVM求解最优解至关重要。
二、SVM的理论基础
上节我们探讨了关于拉格朗日乘子和KKT条件,这为后面SVM求解奠定基础,本节希望通俗的细说一下原理部分。
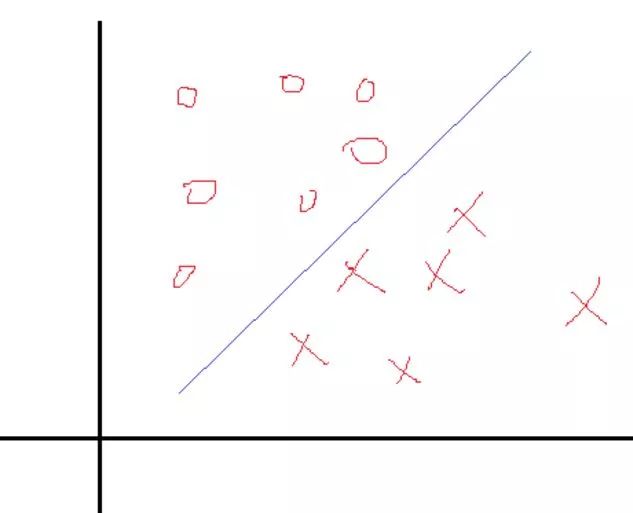
一个简单的二分类问题如下图:
我们希望找到一个决策面使得两类分开,这个决策面一般表示就是W'X+b=0,现在的问题是找到对应的W和b使得分割最好,知道logistic分类 机器学习之logistic回归与分类的可能知道,这里的问题和那里的一样,也是找权值。在那里,我们是根据每一个样本的输出值与目标值得误差不断的调整权值W和b来求得最终的解的。当然这种求解最优的方式只是其中的一种方式。那么SVM的求优方式是怎样的呢?
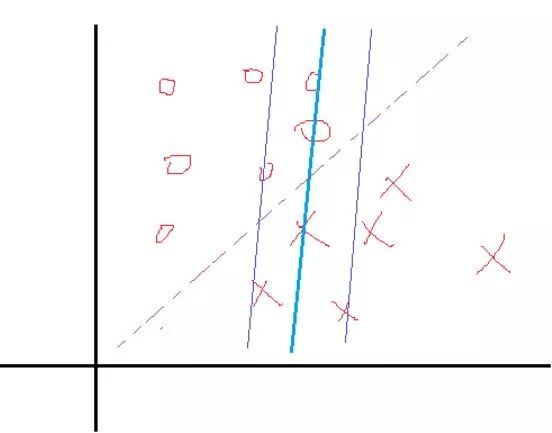
这里我们把问题反过来看,假设我们知道了结果,就是上面这样的分类线对应的权值W和b。那么我们会看到,在这两个类里面,是不是总能找到离这个线最近的点,向下面这样:
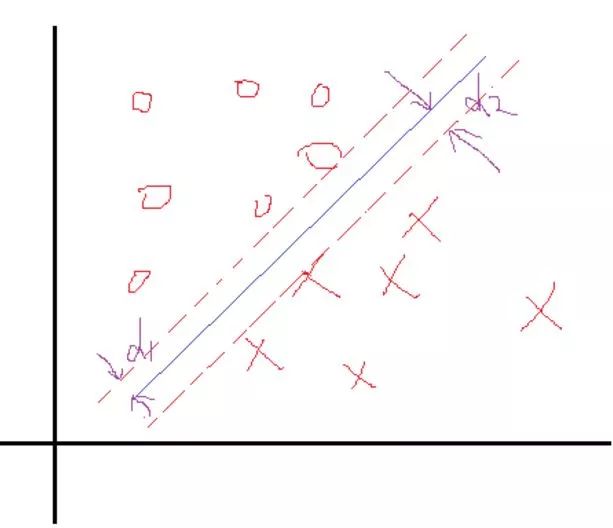
然后定义一下离这个线最近的点到这个分界面(线)的距离分别为d1,d2。那么SVM找最优权值的策略就是,先找到最边上的点,再找到这两个距离之和D,然后求解D的**最大值**,想想如果按照这个策略是不是可以实现最优分类,是的。好了,还是假设找到了这样一个分界面W'X+b=0,那么做离它最近的两类点且平行于分类面,如上面的虚线所示。
好了再假设我们有这两个虚线,那么真实的分界面我们认为正好是这两个分界面的中间线,这样d1就等于d2了。因为真实的分界面为W'X+b=0,那么就把两个虚线分别设置为W'X+b=1和W'X+b=-1,可以看到虚线相对于真实面只是上下移动了1个单位距离,可能会说你怎么知道正好是一个距离?确实不知道,就假设上下是k个距离吧,那么假设上虚线现在为W'X+b=k,两边同时除k可以吧,这样上虚线还是可以变成W'X+b=1,同理下虚线也可以这样,然后他们的中线就是W1'X+b1=0吧,可以看到从k到1,权值无非从w变化到w1,b变到b1,我在让w=w1,b=b1,不是又回到了起点吗,也就是说,这个中间无非是一个倍数关系。
所以我们只需要先确定使得上下等于1的距离,再去找这一组权值,这一组权值会自动变化到一定倍数使得距离为1的。
好了再看看D=d1+d2怎么求吧,假设分界面W'X+b=0,再假设X是两维的,那么分界面再细写出来就是:W1'X1+W2'X2+b=0。上分界线:W1'X1+W2'X2+b=1,这是什么,两条一次函数(y=kx+b)的曲线是不是,那么初中就学过两直线的距离吧,
这里W=(w1,w2),是个向量,||W||为向量的距离,那么||W||^2=W'W。下界面同理。这样
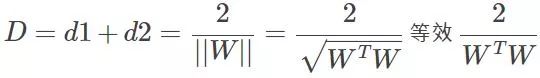
要使D最大,就要使分母最小,这样优化问题就变为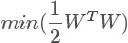
注意的是这可不是一个约束条件,而是对所有的每个样本xi都有一个这样的约束条件。转换到这种形式以后是不是很像上节说到的KKT条件下的优化问题了,就是这个。但是有一个问题,我们说上节的KKT是在凸函数下使用的,那么这里的目标函数是不是呢?答案是的,想想W'*W,函数乘出来应该很单一,不能有很多极点,当然也也可以数学证明是的。
好了那样的话就可以引入拉格朗日乘子法了,优化的目标变为:
然后要求这个目标函数最优解,求导吧,
这两个公式非常重要,简直是核心公式。
求导得到这个应该很简单吧,那我问你为什么W'W 对w求导是w呢?如果你知道,那么你很厉害了,反正开始我是一直没转过来。其实说起来也很简单,如果光去看看为什么求导以后,转置就没了,不太好想明白,设想一下假设现在是二维样本点,也就是最终的W=(w1,w2),那么W'W=w1*w1+w2*w2那么对w1求导就是2w1,对w2就是2w2,这样写在一起就是对w求导得到(2w1,2w2)=2w了,然后乘前面一个1/2(这也就是为什么要加一个1/2),就变成w了。
好了得到上面的两个公式,再带回L中把去w和b消掉,你又可能发现,w确实可以消,因为有等式关系,那b怎么办?上述对b求导的结果竟然不含有b,上天在开玩笑吗?其实没有,虽然没有b,但是有那个求和为0呀,带进去你会惊人的发现,b还真的可以消掉,就是因为了那个等式。简单带下:
那么求解最最开始的函数的最小值等价到这一步以后就是求解W的最大值了,因为使用了拉格朗日乘子法后,原问题就变为其对偶问题了,最小变成了最大,至于为什么,等到详细研究过对偶问题再来解释吧。不了解的,只需要知道求W的极值即可。整理一下,经过这么一圈的转化,最终的问题为:
为什么有ai >0$,这是上节说到的KKT条件的必须。至此问题来源部分到这。
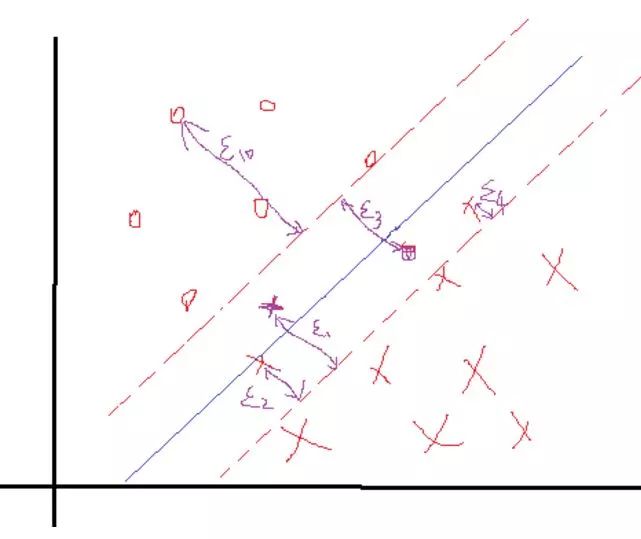
细心的你肯可能会发现,上述所有的构造等等都是在数据完全线性可分,且分界面完全将两类分开,那么如果出现了下面这种情况:
正负两类的最远点没有明显的分解面,搞不好正类的最远点反而会跑到负类里面去了,负类最远点跑到正类里面去了,要是这样的话,你的分界面都找不到,因为你不可能找到将它们完全分开的分界面,那么这些点在实际情况是有的,就是一些离群点或者噪声点,因为这一些点导致整个系统用不了。当然如果不做任何处理确实用不了,但是我们处理一下就可以用了。SVM考虑到这种情况,所以在上下分界面上加入松弛变量e,认为如果正类中有点到上界面的距离小于e,那么认为他是正常的点,哪怕它在上界面稍微偏下一点的位置,同理下界面。还是以上面的情况,我们目测下的是理想的分解面应该是下面这种情况:
如果按照这种分会发现4个离群点,他们到自己对应分界面的距离表示如上,理论上讲,我们给每一个点都给一个自己的松弛变量ei,如果一个分界面求出来了,那么比较这个点到自己对应的界面(上、下界面)的距离是不是小于这个值,要是小于这个值,就认为这个界面分的可以,比如上面的e3这个点,虽然看到明显偏离了正轨,但是计算发现它的距离d小于等于我们给的e3,那么我们说这个分界面可以接受。你可能会说那像上面的e10,距离那么远了,他肯定是大于预设给这个点的ei了对吧,确实是这样的,但是我们还发现什么?这个点是分对了的点呀,所以你管他大不大于预设值,反正不用调整分界面。需要调整分界面的情况是只有当类似e3这样的点的距离大于了e3的时候。
你发现目标函数里面多了一点东西,而加上这个是合理的,我们在优化的同时,也使得总的松弛变量之和最小。常数C决定了松弛变量之和的影响程度,如果越大,影响越严重,那么在优化的时候会更多的注重所有点到分界面的距离,优先保证这个和小。好了将问题写在一起吧:
三、SMO算法原理与实战求解
上节我们讨论到解SVM问题最终演化为求下列带约束条件的问题:
问题的解就是找到一组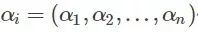
现在我们来看看最初的约束条件是什么样子的:
这是最初的一堆约束条件吧,现在有多少个约束条件就会有多少个
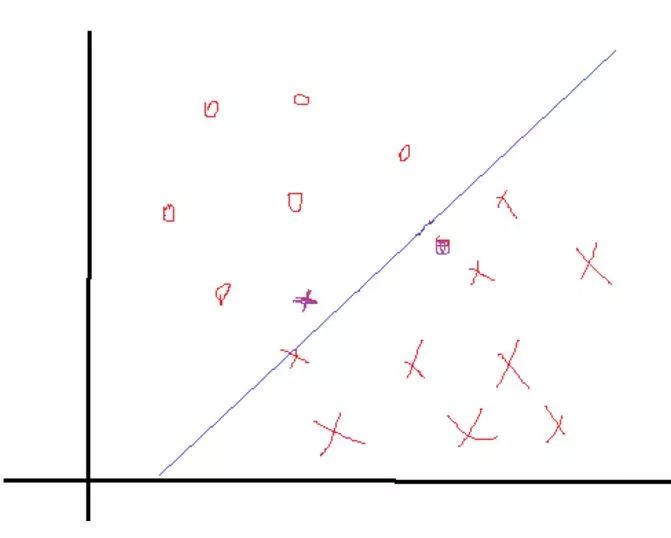
我们知道
某一次迭代后,分类面为粗蓝线所示,上下距离为1的分界面如细蓝线所示,而理想的分界面如紫虚线所示。那么我们想想,要想把粗蓝线变化到紫虚线,在这一次是哪些个点在起作用?很显然是界于细蓝线边上以及它们之间的所有样本点在起作用吧,而对于那些在细蓝线之外的点,比如正类的四个圈和反类的三个叉,它们在这一次的分类中就已经分对了,那还考虑它们干什么?所以这一次就不用考虑这些分对了的点。那么我们用数学公式可以看到,对于在这一次就分对了的点,它们满足什么关系,显然
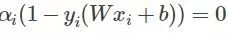
那么满足KKT条件的,我们说如果一个点满足KKT条件,那么它就不需要调整,一旦不满足,就需要调整。由上可知,不满足KKT条件的也有三种情况:
至此我们可以说,简单的,线性的,带有松弛条件(可以容错的)的整个SMO算法就完了,剩下的就是循环,选择两个
当然了,这里面还有些问题就是如何去优化这些步骤,最明显的就是怎么去选择这两个
先不管那么多,就先让他盲目盲目的找吧,设置一个代数,盲目到一定代数停止就ok了,下面就来一个盲目找
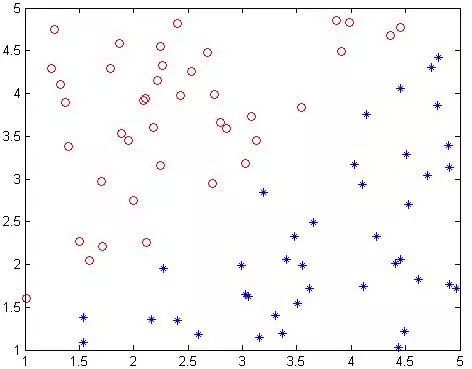
我的样本是这样的:
程序如下:
%%
% * svm 简单算法设计
%
%% 加载数据
% * 最终data格式:m*n,m样本数,n维度
% * label:m*1 标签必须为-1与1这两类
clc
clear
close all
data = load('data_test2.mat');
data = data.data;
train_data = data(1:end-1,:)';
label = data(end,:)';
[num_data,d] = size(train_data);
data = train_data;
%% 定义向量机参数
alphas = zeros(num_data,1);
% 系数
b = 0;
% 松弛变量影响因子
C = 0.6;
iter = 0;
max_iter = 40;
%%
while iter < max_iter
alpha_change = 0;
for i = 1:num_data
%输出目标值
pre_Li = (alphas.*label)'*(data*data(i,:)') + b;
%样本i误差
Ei = pre_Li - label(i);
% 满足KKT条件
if (label(i)*Ei<-0.001 && alphas(i)<C)||(label(i)*Ei>0.001 && alphas(i)>0)
% 选择一个和 i 不相同的待改变的alpha(2)--alpha(j)
j = randi(num_data,1);
if j == i
temp = 1;
while temp
j = randi(num_data,1);
if j ~= i
temp = 0;
end
end
end
% 样本j的输出值
pre_Lj = (alphas.*label)'*(data*data(j,:)') + b;
%样本j误差
Ej = pre_Lj - label(j);
%更新上下限
if label(i) ~= label(j) %类标签相同
L = max(0,alphas(j) - alphas(i));
H = min(C,C + alphas(j) - alphas(i));
else
L = max(0,alphas(j) + alphas(i) -C);
H = min(C,alphas(j) + alphas(i));
end
if L==H %上下限一样结束本次循环
continue;end
%计算eta
eta = 2*data(i,:)*data(j,:)'- data(i,:)*data(i,:)' - ...
data(j,:)*data(j,:)';
%保存旧值
alphasI_old = alphas(i);
alphasJ_old = alphas(j);
%更新alpha(2),也就是alpha(j)
alphas(j) = alphas(j) - label(j)*(Ei-Ej)/eta;
%限制范围
if alphas(j) > H
alphas(j) = H;
elseif alphas(j) < L
alphas(j) = L;
end
%如果alpha(j)没怎么改变,结束本次循环
if abs(alphas(j) - alphasJ_old)<1e-4
continue;end
%更新alpha(1),也就是alpha(i)
alphas(i) = alphas(i) + label(i)*label(j)*(alphasJ_old-alphas(j));
%更新系数b
b1 = b - Ei - label(i)*(alphas(i)-alphasI_old)*data(i,:)*data(i,:)'-...
label(j)*(alphas(j)-alphasJ_old)*data(i,:)*data(j,:)';
b2 = b - Ej - label(i)*(alphas(i)-alphasI_old)*data(i,:)*data(j,:)'-...
label(j)*(alphas(j)-alphasJ_old)*data(j,:)*data(j,:)';
%b的几种选择机制
if alphas(i)>0 && alphas(i)<C
b = b1;
elseif alphas(j)>0 && alphas(j)<C
b = b2;
else
b = (b1+b2)/2;
end
%确定更新了,记录一次
alpha_change = alpha_change + 1;
end
end
% 没有实行alpha交换,迭代加1
if alpha_change == 0
iter = iter + 1;
%实行了交换,迭代清0
else
iter = 0;
end
disp(['iter ================== ',num2str(iter)]);
end
%% 计算权值W
W = (alphas.*label)'*data;
%记录支持向量位置
index_sup = find(alphas ~= 0);
%计算预测结果
predict = (alphas.*label)'*(data*data') + b;
predict = sign(predict);
%% 显示结果
figure;
index1 = find(predict==-1);
data1 = (data(index1,:))';
plot(data1(1,:),data1(2,:),'+r');
hold on
index2 = find(predict==1);
data2 = (data(index2,:))';
plot(data2(1,:),data2(2,:),'*');
hold on
dataw = (data(index_sup,:))';
plot(dataw(1,:),dataw(2,:),'og','LineWidth',2);
% 画出分界面,以及b上下正负1的分界面
hold on
k = -W(1)/W(2);
x = 1:0.1:5;
y = k*x + b;
plot(x,y,x,y-1,'r--',x,y+1,'r--');
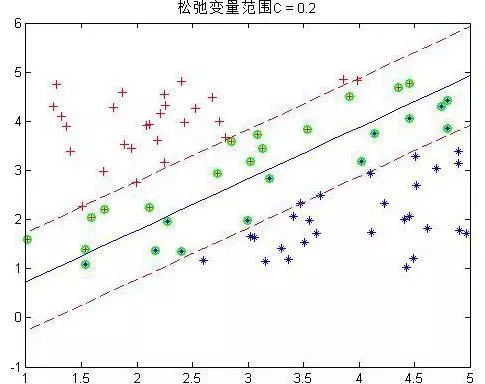
title(['松弛变量范围C = ',num2str(C)]);
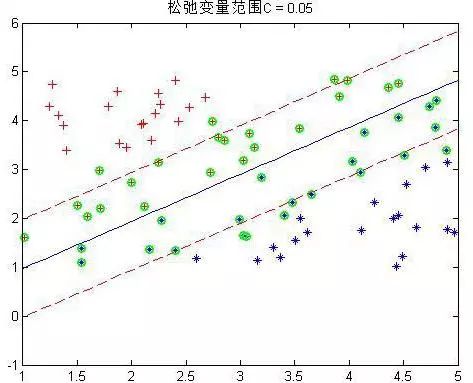
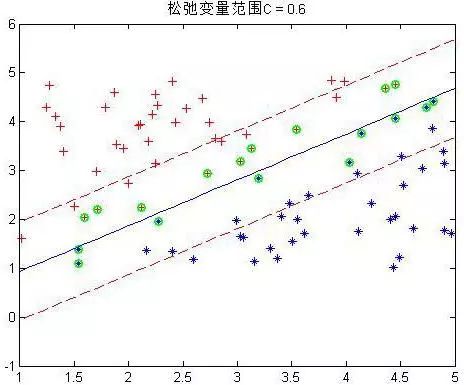
程序中设置了松弛变量前的系数C是事先规定的,表明松弛变量项的影响程度大小。下面是几个不同C下的结果:
这是80个样本点,matlab下还是挺快2秒左右就好了。上图中,把真实分界面,上下范围为1的界面,以及那些α不为0的点(绿色标出)都画了出来,可以看到,C越大,距离越起作用,那么落在分界线之间的点就越少。同时可以看到,三种情况下,真实的分界面(蓝色)都可以将两种样本完全分开(我的样本并没有重叠,也就是完全是可分的)。
好了,这就是随机选取α的实验,第一个α是按顺序遍历所有的α,第二个α是在剩下的α中在随机选一个。当第二个α选了iter次还没有发现不满足KKT条件的,就退出循环。同时程序中的KKT条件略有不同,不过是一样的。下面介绍如何进行启发式的选取α呢?我们分析分析,比如上一次的一些点的α在0-C之间,也就是这些点不满足条件需要调整,那么一次循环后,他调整了一点,在下一次中这些点是不是还是更有可能不满足条件,因为每一次的调整比较不可能完全。而那些在上一次本身满足条件的点,那么在下一次后其实还是更有可能满足条件的。所以在启发式的寻找α过程中,我们并不是遍历所有的点的α,而是遍历那些在0-C之间的α,而0-C反应到点上就是那些属于边界之间的点是不是。当某次遍历在0-C之间找不到α了,那么我们再去整体遍历一次,这样就又会出现属于边界之间α了,然后再去遍历这些α,如此循环。那么在遍历属于边界之间α的时候,因为是需要选两个α的,第一个可以随便选,那第二个呢?这里在用一个启发式的思想,第1个α选择后,其对应的点与实际标签是不是有一个误差,属于边界之间α的所以点每个点都会有一个自己的误差,这个时候选择剩下的点与第一个α点产生误差之差最大的那个点。
程序如下:
%%
% * svm 简单算法设计 --启发式选择
%
%% 加载数据
% * 最终data格式:m*n,m样本数,n维度
% * label:m*1 标签必须为-1与1这两类
clc
clear
close all
data = load('data_test2.mat');
data = data.data;
train_data = data(1:end-1,:)';
label = data(end,:)';
[num_data,d] = size(train_data);
data = train_data;
%% 定义向量机参数
alphas = zeros(num_data,1);
b = 0;
error = zeros(num_data,2);
tol = 0.001;
C = 0.6;
iter = 0;
max_iter = 40;
%%
alpha_change = 0;
entireSet = 1;%作为一个标记看是选择全遍历还是部分遍历
while (iter < max_iter) && ((alpha_change > 0) || entireSet)
alpha_change = 0;
%% -----------全遍历样本-------------------------
if entireSet
for i = 1:num_data
Ei = calEk(data,alphas,label,b,i);%计算误差
if (label(i)*Ei<-0.001 && alphas(i)<C)||...
(label(i)*Ei>0.001 && alphas(i)>0)
%选择下一个alphas
[j,Ej] = select(i,data,num_data,alphas,label,b,C,Ei,entireSet);
alpha_I_old = alphas(i);
alpha_J_old = alphas(j);
if label(i) ~= label(j)
L = max(0,alphas(j) - alphas(i));
H = min(C,C + alphas(j) - alphas(i));
else
L = max(0,alphas(j) + alphas(i) -C);
H = min(C,alphas(j) + alphas(i));
end
if L==H
continue;end
eta = 2*data(i,:)*data(j,:)'- data(i,:)*...
data(i,:)' - data(j,:)*data(j,:)';
if eta >= 0
continue;end
alphas(j) = alphas(j) - label(j)*(Ei-Ej)/eta;
%限制范围
if alphas(j) > H
alphas(j) = H;
elseif alphas(j) < L
alphas(j) = L;
end
if abs(alphas(j) - alpha_J_old) < 1e-4
continue;end
alphas(i) = alphas(i) + label(i)*...
label(j)*(alpha_J_old-alphas(j));
b1 = b - Ei - label(i)*(alphas(i)-alpha_I_old)*...
data(i,:)*data(i,:)'- label(j)*...
(alphas(j)-alpha_J_old)*data(i,:)*data(j,:)';
b2 = b - Ej - label(i)*(alphas(i)-alpha_I_old)*...
data(i,:)*data(j,:)'- label(j)*...
(alphas(j)-alpha_J_old)*data(j,:)*data(j,:)';
if (alphas(i) > 0) && (alphas(i) < C)
b = b1;
elseif (alphas(j) > 0) && (alphas(j) < C)
b = b2;
else
b = (b1+b2)/2;
end
alpha_change = alpha_change + 1;
end
end
iter = iter + 1;
%% --------------部分遍历(alphas=0~C)的样本--------------------------
else
index = find(alphas>0 & alphas < C);
for ii = 1:length(index)
i = index(ii);
Ei = calEk(data,alphas,label,b,i);%计算误差
if (label(i)*Ei<-0.001 && alphas(i)<C)||...
(label(i)*Ei>0.001 && alphas(i)>0)
%选择下一个样本
[j,Ej] = select(i,data,num_data,alphas,label,b,C,Ei,entireSet);
alpha_I_old = alphas(i);
alpha_J_old = alphas(j);
if label(i) ~= label(j)
L = max(0,alphas(j) - alphas(i));
H = min(C,C + alphas(j) - alphas(i));
else
L = max(0,alphas(j) + alphas(i) -C);
H = min(C,alphas(j) + alphas(i));
end
if L==H
continue;end
eta = 2*data(i,:)*data(j,:)'- data(i,:)*...
data(i,:)' - data(j,:)*data(j,:)';
if eta >= 0
continue;end
alphas(j) = alphas(j) - label(j)*(Ei-Ej)/eta;
%限制范围
if alphas(j) > H
alphas(j) = H;
elseif alphas(j) < L
alphas(j) = L;
end
if abs(alphas(j) - alpha_J_old) < 1e-4
continue;end
alphas(i) = alphas(i) + label(i)*...
label(j)*(alpha_J_old-alphas(j));
b1 = b - Ei - label(i)*(alphas(i)-alpha_I_old)*...
data(i,:)*data(i,:)'- label(j)*...
(alphas(j)-alpha_J_old)*data(i,:)*data(j,:)';
b2 = b - Ej - label(i)*(alphas(i)-alpha_I_old)*...
data(i,:)*data(j,:)'- label(j)*...
(alphas(j)-alpha_J_old)*data(j,:)*data(j,:)';
if (alphas(i) > 0) && (alphas(i) < C)
b = b1;
elseif (alphas(j) > 0) && (alphas(j) < C)
b = b2;
else
b = (b1+b2)/2;
end
alpha_change = alpha_change + 1;
end
end
iter = iter + 1;
end
%% --------------------------------
if entireSet %第一次全遍历了,下一次就变成部分遍历
entireSet = 0;
elseif alpha_change == 0
%如果部分遍历所有都没有找到需要交换的alpha,再改为全遍历
entireSet = 1;
end
disp(['iter ================== ',num2str(iter)]);
end
%% 计算权值W
W = (alphas.*label)'*data;
%记录支持向量位置
index_sup = find(alphas ~= 0);
%计算预测结果
predict = (alphas.*label)'*(data*data') + b;
predict = sign(predict);
%% 显示结果
figure;
index1 = find(predict==-1);
data1 = (data(index1,:))';
plot(data1(1,:),data1(2,:),'+r');
hold on
index2 = find(predict==1);
data2 = (data(index2,:))';
plot(data2(1,:),data2(2,:),'*');
hold on
dataw = (data(index_sup,:))';
plot(dataw(1,:),dataw(2,:),'og','LineWidth',2);
% 画出分界面,以及b上下正负1的分界面
hold on
k = -W(1)/W(2);
x = 1:0.1:5;
y = k*x + b;
plot(x,y,x,y-1,'r--',x,y+1,'r--');
title(['松弛变量范围C = ',num2str(C)]);
其中的子函数,一个是计算误差函数,一个是选择函数如下:
function Ek = calEk(data,alphas,label,b,k)
pre_Li = (alphas.*label)'*(data*data(k,:)') + b;
Ek = pre_Li - label(k);
function [J,Ej] = select(i,data,num_data,alphas,label,b,C,Ei,choose)
maxDeltaE = 0;maxJ = -1;
if choose == 1 %全遍历---随机选择alphas
j = randi(num_data ,1);
if j == i
temp = 1;
while temp
j = randi(num_data,1);
if j ~= i
temp = 0;
end
end
end
J = j;
Ej = calEk(data,alphas,label,b,J);
else %部分遍历--启发式的选择alphas
index = find(alphas>0 & alphas < C);
for k = 1:length(index)
if i == index(k)
continue;
end
temp_e = calEk(data,alphas,label,b,k);
deltaE = abs(Ei - temp_e); %选择与Ei误差最大的alphas
if deltaE > maxDeltaE
maxJ = k;
maxDeltaE = deltaE;
Ej = temp_e;
end
end
J = maxJ;
end
至此算是完了,试验了一下,两者的效果其实差不多(反而随机选取的效果更好一点,感觉是因为随机保证了更多的可能,毕竟随机选择包括了你的特殊选择,但是特殊选择到后期是特殊不起来的,反而随机会把那些差一点的选择出来),但是速度上当样本小的时候,基本上差不多,但是当样本大的时候,启发式的特殊选择明显占优势了。我试验了400个样本点的情况,随机选择10多秒把,而启发式2,3秒就好了。可见效果差不多的情况下,启发式选择是首要选择。
至此两种方式下的方法都实验完了。那么我们看到,前面(三节)所讲的一切以及实验,分类的样本都是线性样本,那么如果来了非线性样本该如何呢?而SVM的强大之处更在于对非线性样本的准确划分。那么前面的理论对于非线性样本是否适用?我们又该如何处理非线性样本呢?请看下节SVM非线性样本的分类。
四、SVM非线性分类原理实验
前面几节我们讨论了SVM原理、求解线性分类下SVM的SMO方法。本节将分析SVM处理非线性分类的相关问题。
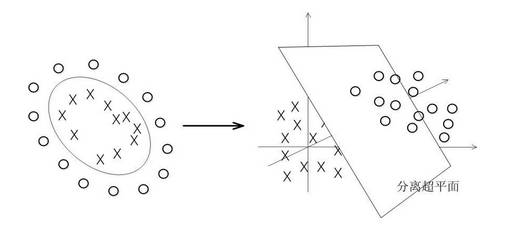
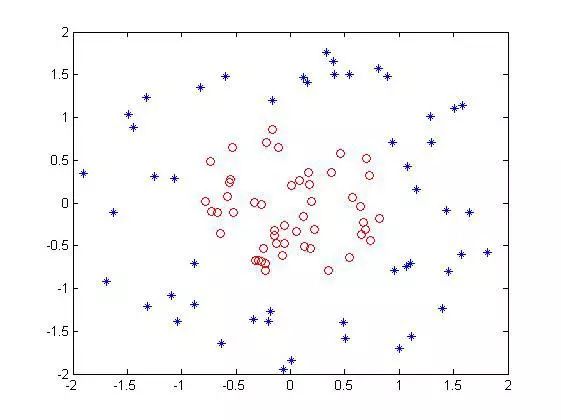
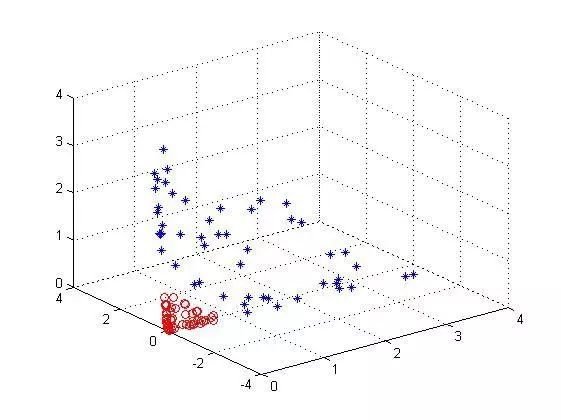
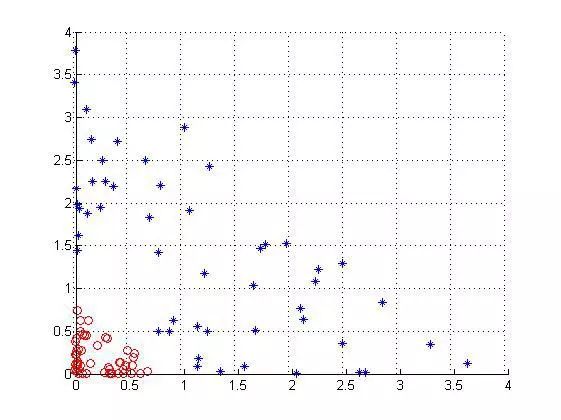
一般的非线性分类如下左所示(后面我们将实战下面这种情况):
可以看到在原始空间中你想用一个直线分类面划分开来是不可能了,除非圆。而当你把数据点映射一下成右图所示的情况后,现在数据点明显看上去是线性可分的,那么在这个空间上的数据点我们再用前面的SVM算法去处理,就可以得到每个数据点的分类情况了,而这个分类情况也是我们在低维空间的情况。也就是说,单纯的SVM是不能处理非线性问题的,说白了只能处理线性问题,但是来了非线性样本怎么办呢?我们是在样本上做的文章,我把非线性样本变成线性样本,再去把变化后的线性样本拿去分类,经过这么一圈,就达到了把非线性样本分开的目的,所以只看开头和结尾的话发现,SVM竟然可以分非线性问题,其实呢还是分的线性问题。
现在的问题是如何找到这个映射关系对吧,就比如上面那个情况,我们可以人为计算出这种映射,比如一个样本点是用坐标表示的(x1,x2),它有个类标签,假设为1,那么把这个点映射到三维中变成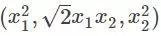
然后按照上面那个公式去把每个点映射成3维坐标点后,画出来是这样的:
可以看到是线性可分的吧,如果还看不清把视角换个角度(右视图):
现在能看清楚了吧。那这是二维的点到三维,映射的关系就是上面的那个关系,那如果是三维到四维,四维到N维呢?这个关系你还想去找吗?理论上是找的到的,但是实际上人工去找你怎么去找?你怎么知道数据的映射关系是这样的是那样的?不可能知道。然而我们真的需要找到这种关系吗?答案是不需要的,返回去看看前三节的关于SVM的理论部分可以看到,无论是计算a呀,还是b呀等等,只要涉及到原始数据点的,都是以内积的形式出来的,也就是说是一个点的向量与另一个点的向量相乘的,向量内积出来是一个值。
就拿a来更新来说,如下:
最后也是得到一个值比如C2。既然SVM里面所有涉及到原始数据的地方都是以向量的形式出现的,那么我们还需要管它的映射关系吗?因为它也不需要你去计算说具体到比如说三维以后,三维里面的三个坐标值究竟是多少,他需要的是内积以后的一个结果值。那么好办了,我就假设有一个黑匣子,输入原始数据维度下的两个坐标向量,然后经过黑匣子这么一圈,出来一个值,这个值我们就认为是高维度下的值。而黑匣子的潜在意义就相当于一个高维映射器一样。更重要的是我们并不需要知道黑匣子究竟是怎么映射的,只需要知道它的低纬度下的形式就可以了。常用的黑匣子就是径向基函数,而这个黑匣子在数学上就叫做核函数,例如径向基函数的外在形式如下所示:
o是需要预先设定的参数。至于这个黑匣子把初始数据映射到多少维了,谁知道呢,既然是黑匣子,那就是看不到的,上帝给了人类这么一个黑匣子就已经很够意思了。可以看到的是原始数据结果黑匣子算了以后,出来就是一个值了,而这个值就认为是高维度下的数据通过内积计算而来的值。当然上帝还留了一个窗户,就是
好了既然黑匣子是藏着的,那也就只能说这么多了。有趣的是上帝给的这个黑匣子不止一个,有好几个,只是上面的那个普遍效果更好而已。基于此,那么对于上节的SMO算法,如果拿来求解非线性数据的话,我们只需要将其中对应的内积部分改成核函数的形式即可。一个数据核函数程序如下:
function result = Kernel(data1,data2,sigma)
% data里面每一行数据是一个样本(的行向量)
[m1,~] = size(data1);
[m2,~] = size(data2);
result = zeros(m1,m2);
for i = 1:m1
for j = 1:m2
result(i,j) = exp(-norm(data1(i,:)-data2(j,:))/(2*sigma^2));
end
end
有了此核函数,我们用上节的随机遍历
α
然后把主程序对应的部分用上述核函数代替:
%%
% * svm 简单算法设计
%
%% 加载数据
% * 最终data格式:m*n,m样本数,n维度
% * label:m*1 标签必须为-1与1这两类
clc
clear
% close all
data = load('data_test1.mat');
data = data.data;
train_data = data(1:end-1,:)';
label = data(end,:)';
[num_data,d] = size(train_data);
data = train_data;
%% 定义向量机参数
alphas = zeros(num_data,1);
% 系数
b = 0;
% 松弛变量影响因子
C = 0.6;
iter = 0;
max_iter = 80;
% 核函数的参数
sigma = 4;
%%
while iter < max_iter
alpha_change = 0;
for i = 1:num_data
%输出目标值
pre_Li = (alphas.*label)'*Kernel(data,data(i,:),sigma) + b;
%样本i误差
Ei = pre_Li - label(i);
% 满足KKT条件
if (label(i)*Ei<-0.001 && alphas(i)<C)||(label(i)*Ei>0.001 && alphas(i)>0)
% 选择一个和 i 不相同的待改变的alpha(2)--alpha(j)
j = randi(num_data,1);
if j == i
temp = 1;
while temp
j = randi(num_data,1);
if j ~= i
temp = 0;
end
end
end
% 样本j的输出值
pre_Lj = (alphas.*label)'*Kernel(data,data(j,:),sigma) + b;
%样本j误差
Ej = pre_Lj - label(j);
%更新上下限
if label(i) ~= label(j) %类标签相同
L = max(0,alphas(j) - alphas(i));
H = min(C,C + alphas(j) - alphas(i));
else
L = max(0,alphas(j) + alphas(i) -C);
H = min(C,alphas(j) + alphas(i));
end
if L==H %上下限一样结束本次循环
continue;end
%计算eta
eta = 2*Kernel(data(i,:),data(j,:),sigma)- ...
Kernel(data(i,:),data(i,:),sigma)...
- Kernel(data(j,:),data(j,:),sigma);
%保存旧值
alphasI_old = alphas(i);
alphasJ_old = alphas(j);
%更新alpha(2),也就是alpha(j)
alphas(j) = alphas(j) - label(j)*(Ei-Ej)/eta;
%限制范围
if alphas(j) > H
alphas(j) = H;
elseif alphas(j) < L
alphas(j) = L;
end
%如果alpha(j)没怎么改变,结束本次循环
if abs(alphas(j) - alphasJ_old)<1e-4
continue;end
%更新alpha(1),也就是alpha(i)
alphas(i) = alphas(i) + label(i)*label(j)*(alphasJ_old-alphas(j));
%更新系数b
b1 = b - Ei - label(i)*(alphas(i)-alphasI_old)*...
Kernel(data(i,:),data(i,:),sigma) - label(j)*...
(alphas(j)-alphasJ_old)*Kernel(data(i,:),data(j,:),sigma);
b2 = b - Ej - label(i)*(alphas(i)-alphasI_old)*...
Kernel(data(i,:),data(j,:),sigma)- label(j)*...
(alphas(j)-alphasJ_old)*Kernel(data(j,:),data(j,:),sigma);
%b的几种选择机制
if alphas(i)>0 && alphas(i)<C
b = b1;
elseif alphas(j)>0 && alphas(j)<C
b = b2;
else
b = (b1+b2)/2;
end
%确定更新了,记录一次
alpha_change = alpha_change + 1;
end
end
% 没有实行alpha交换,迭代加1
if alpha_change == 0
iter = iter + 1;
%实行了交换,迭代清0
else
iter = 0;
end
disp(['iter ================== ',num2str(iter)]);
end
%% 计算权值W
% W = (alphas.*label)'*data;
%记录支持向量位置
index_sup = find(alphas ~= 0);
%计算预测结果
predict = (alphas.*label)'*Kernel(data,data,sigma) + b;
predict = sign(predict);
%% 显示结果
figure;
index1 = find(predict==-1);
data1 = (data(index1,:))';
plot(data1(1,:),data1(2,:),'+r');
hold on
index2 = find(predict==1);
data2 = (data(index2,:))';
plot(data2(1,:),data2(2,:),'*');
hold on
dataw = (data(index_sup,:))';
plot(dataw(1,:),dataw(2,:),'og','LineWidth',2);
title(['核函数参数sigma = ',num2str(sigma)]);
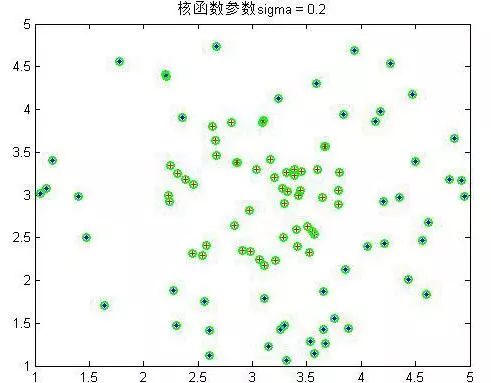
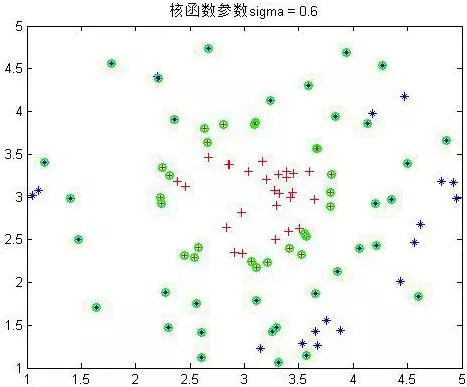
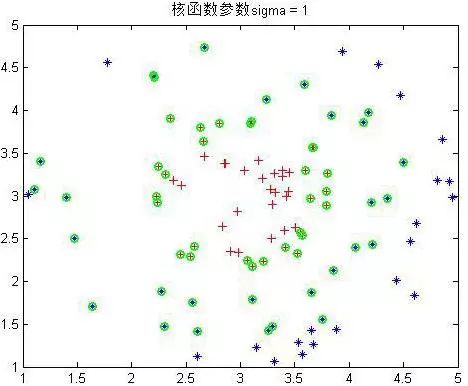
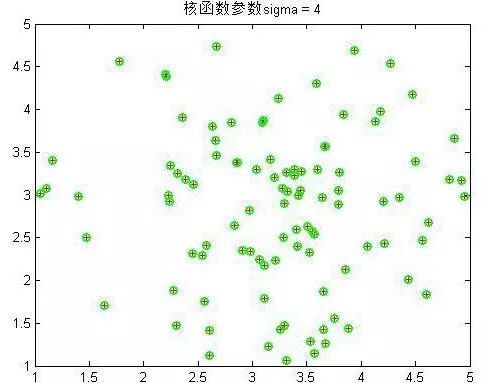
下面是几个不同参数下的结果:
可以看到
σ到4以后就分不出来了。绿色的为支持向量,可以看到在
σ在0.6到1之间是最少的,结果应该也是最好的。至此SMO实验非线性样本完毕。
当今学者已经有非常多的人研究SVM算法,同时开发了许多开源的程序,这些程序都是经过不断优化的,性能比起我们这里自己编的来说要好得多,所以在实际应用中通常都是用他们无私贡献的软件包。一个典型的软件包就是台湾一个教授团队的LIBSVM软件包,那么你是否想一窥其用法,看看它的性能如何呢?请看下节matlab下LIBSVM的简单使用。
五、MATLAB下libsvm的简单使用:分类与回归
本节简单介绍一下libsvm的使用方法。关于libsvm似乎曾经使用过,那个时候主要用libsvm进行简单的人脸识别实验。
1)介绍与分类实验
那么现在最新版本的libsvm为3.2.0,下载地址如下: http://www.csie.ntu.edu.tw/~cjlin/libsvm/
下载下来的libsvm其实包含好多个平台的工具箱软件,c++,matlab,java,python都有。他们的函数使用方法是一样的。
那么在下载完以后,点击里面的matlab下平台,直接在点击里面的make.m函数就可以了。正常情况下如果你的matlab含有编译平台的话直接就可以运行了,如果没有,还需要选择一个平台 mex -setup 。小提醒一下,这个编译过程不要在c盘下使用,也就是libsvm先不要放在c盘,涉及到权限,机器不让编译。编译完后在matlab的设置路径中添加进去编译的文件夹及其内容,那么就可以使用了。正常编译的过程是这样的: 在上面的人脸识别实验中曾经介绍过里面的主要函数,这里为了放在一块,把那里的拿过来吧:
目前版LIBSVM(3.2.0)在matlab下编译完后只有四个函数,libsvmread,Libsvmwrite,svmtrain(matlab自带的工具箱中有一个同名的函数),svmpredict。
libsvmread主要用于读取数据
这里的数据是非matlab下的.mat数据,比如说是.txt,.data等等,这个时候需要使用libsvmread函数进行转化为matlab可识别数据,比如自带的数据是heart_scale数据,那么导入到matlab有两种方式,一种使用libsvmread函数,在matlab下直接libsvmread(heart_scale);第二种方式为点击matlab的‘导入数据’按钮,然后导向heart_scale所在位置,直接选择就可以了。个人感觉第二种方式超级棒,无论对于什么数据,比如你在哪个数据库下下载的数据,如何把它变成matlab下数据呢?因为有的数据libsvmread读取不管用,但是‘导入数据’后就可以变成matlab下数据。
libsvmwrite写函数,就是把已知数据存起来
使用方式为:libsvmwrite(‘filename’,label_vector, instance_matrix);
label_vector是标签,instance_matrix为数据矩阵(注意这个数据必须是稀疏矩阵,就是里面的数据不包含没用的数据(比如很多0),有这样的数据应该去掉再存)。
svmtrain训练函数,训练数据产生模型的
一般直接使用为:model=svmtrain(label,data,cmd); label为标签,data为训练数据(数据有讲究,每一行为一个样本的所有数据,列数代表的是样本的个数),每一个样本都要对应一个标签(分类问题的话一般为二分类问题,也就是每一个样本对应一个标签)。cmd为相应的命令集合,都有哪些命令呢?很多,-v,-t,-g,-c,等等,不同的参数代表的含义不同,比如对于分类问题,这里-t就表示选择的核函数类型,-t=0时线性核。-t=1多项式核,-t=2,径向基函数(高斯),-t=3,sigmod核函数,新版出了个-t=4,预计算核(还不会用);-g为核函数的参数系数,-c为惩罚因子系数,-v为交叉验证的数,默认为5,这个参数在svmtrain写出来使用与不写出来不使用的时候,model出来的东西不一样,不写的时候,model为一个结构体,是一个模型,可以带到svmpredict中直接使用,写出来的时候,出来的是一个训练模型的准确率,为一个数值。一般情况下就这几个参数重要些,还有好多其他参数,可以自己参考网上比较全的,因为下面的这种方法的人脸识别就用到这么几个参数,其他的就不写了。
svmpredict训练函数,使用训练的模型去预测来的数据类型。
使用方式为:
[predicted_label,accuracy,decision_values/prob_estimates]= svmpredict(testing_label_vector,testing_instance_matrix,model,’libsvm_options’)
或者:
[predicted_label]=svmpredict(testing_label_vector,testing_instance_matrix, model, ‘libsvm_options’)
第一种方式中,输出为三个参数,预测的类型,准确率,评估值(非分类问题用着),输入为测试类型(这个可与可无,如果没有,那么预测的准确率accuracy就没有意义了,如果有,那么就可以通过这个值与预测出来的那个类型值相比较得出准确率accuracy,但是要说明一点的是,无论这个值有没有,在使用的时候都得加上,即使没有,也要随便加上一个类型值,反正你也不管它对不对,这是函数使用所规定的的),再就是输入数据值,最后是参数值(这里的参数值只有两种选择,-p和-b参数),曾经遇到一个这样的问题,比如说我在训练函数中规定了-g参数为0.1,那么在预测的时候是不是也要规定这个参数呢?当你规定了以后,程序反而错误,提醒没有svmpredict的-g参数,原因是在svmtrain后会出现一个model,而在svmpredict中你已经用了这个model,而这个model中就已经包含了你所有的训练参数了,所以svmpredict中没有这个参数,那么对于的libsvm_options就是-p和-b参数了。对于函数的输出,两种方式调用的方法不一样,第一种调用把所有需要的数据都调用出来了,二第二种调用,只调用了predicted_label预测的类型,这里我们可以看到,在单纯的分类预测模型中,其实第二种方式更好一些吧,既简单有实用。
致此,四个函数在分类问题中的介绍大概如此,当然还有很多可以优化的细节就不详细说了,比如可以再使用那些参数的时候,你如果不规定参数的话,所有的-参数都是使用默认的,默认的就可能不是最好的吧,这样就涉及到如何去优化这个参数了。
使用就介绍到这里吧,下面实战一下,样本集选择前面使用的200个非线性样本集,函数如下:
%%
% * libsvm 工具箱简单使用
%
%% 加载数据
% * 最终data格式:m*n,m样本数,n维度
% * label:m*1 标签为-1与1这两类
clc
clear
close all
data = load('data_test1.mat');
data = data.data';
%选择训练样本个数
num_train = 80;
%构造随机选择序列
choose = randperm(length(data));
train_data = data(choose(1:num_train),:);
gscatter(train_data(:,1),train_data(:,2),train_data(:,3));
label_train = train_data(:,end);
test_data = data(choose(num_train+1:end),:);
label_test = test_data(:,end);
predict = zeros(length(test_data),1);
%% ----训练模型并预测分类
model = svmtrain(label_train,train_data(:,1:end-1),'-t 2');
% -t = 2 选择径向基函数核
true_num = 0;
for i = 1:length(test_data)
% 作为预测,svmpredict第一个参数随便给个就可以
predict(i) = svmpredict(1,test_data(i,1:end-1),model);
end
%% 显示结果
figure;
index1 = find(predict==1);
data1 = (test_data(index1,:))';
plot(data1(1,:),data1(2,:),'or');
hold on
index2 = find(predict==-1);
data2 = (test_data(index2,:))';
plot(data2(1,:),data2(2,:),'*');
hold on
indexw = find(predict~=(label_test));
dataw = (test_data(indexw,:))';
plot(dataw(1,:),dataw(2,:),'+g','LineWidth',3);
accuracy = length(find(predict==label_test))/length(test_data);
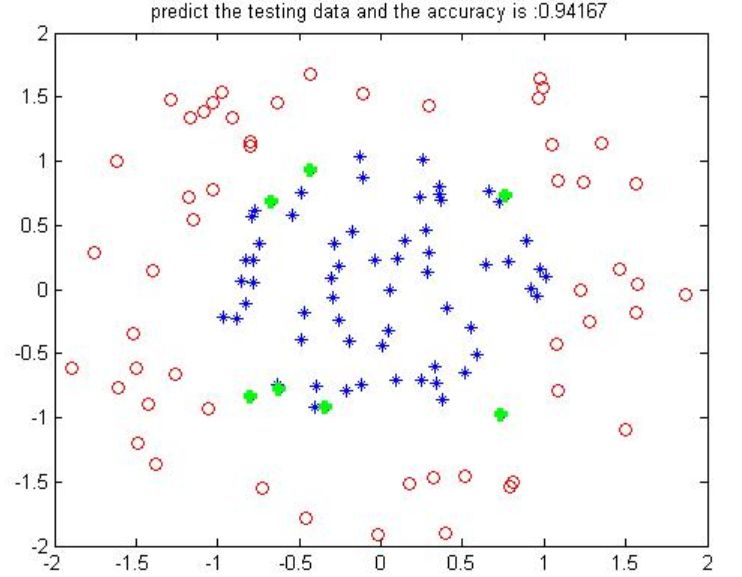
title(['predict the testing data and the accuracy is :',num2str(accuracy)]);
可以看到,关于svm的部分就那么一点,其他的都是辅助吧,那么一个结果如下:
数据人为设置了一些重叠,这个结果算是非常好了。当然对于libsvm函数,里面还有许多细节,像参数选择等等,不同的参数结果是不一样的,这就待你去探究了。
2)回归实验
回归问题不像分类问题,回归问题相当于根据训练样本训练出一个拟合函数一样,可以根据这个拟合函数可以来预测给定一个样本的输出值。可以看到分类问题输出的是样本所属于的类,而回归问题输出的是样本的预测值。
常用的地方典型的比如股票预测,人口预测等等此类预测问题。
libsvm同样可以进行回归预测,所需要改变的只是里面的参数设置。查看libsvm的官网介绍参数详情如下:
options:
-s svm_type : set type of SVM (default 0)
0 -- C-SVC
1 -- nu-SVC
2 -- one-class SVM
3 -- epsilon-SVR
4 -- nu-SVR
-t kernel_type : set type of kernel function (default 2)
0 -- linear: u'*v
1 -- polynomial: (gamma*u'*v + coef0)^degree
2 -- radial basis function: exp(-gamma*|u-v|^2)
3 -- sigmoid: tanh(gamma*u'*v + coef0)
-d degree : set degree in kernel function (default 3)
-g gamma : set gamma in kernel function (default 1/num_features)
-r coef0 : set coef0 in kernel function (default 0)
-c cost : set the parameter C of C-SVC, epsilon-SVR, and nu-SVR (default 1)
-n nu : set the parameter nu of nu-SVC, one-class SVM, and nu-SVR (default 0.5)
-p epsilon : set the epsilon in loss function of epsilon-SVR (default 0.1)
-m cachesize : set cache memory size in MB (default 100)
-e epsilon : set tolerance of termination criterion (default 0.001)
-h shrinking: whether to use the shrinking heuristics, 0 or 1 (default 1)
-b probability_estimates: whether to train a SVC or SVR model for probability estimates, 0 or 1 (default 0)
-wi weight: set the parameter C of class i to weight*C, for C-SVC (default 1)
可以看到-s svm_type 控制的就是训练类型,而当-s等于3或4的时候,就是回归模型SVR。
-s 3 就是常用的带惩罚项的 SVR模型,我们用这个实验。我使用的是libsvm3.2.0工具箱,版本不同可能会带来调用方式的不同。测试实验的代码如下,可能会有一些细节需要自己去探索:
close all;
clear;
clc;
%%
% 生成待回归的数据
x = (-1:0.1:1)';
y = -100*x.^3 + x.^2 - x + 1;
% 加点噪声
y = y+ 20*rand(length(y),1);
%% 采用交叉验证选择参数
mse = 10^7;
for log2c = -10:0.5:3,
for log2g = -10:0.5:3,
% -v 交叉验证参数:在训练的时候需要,测试的时候不需要,否则出错
cmd = ['-v 3 -c ', num2str(2^log2c), ' -g ', num2str(2^log2g) , ' -s 3 -p 0.4 -t 3'];
cv = svmtrain(y,x,cmd);
if (cv < mse),
mse = cv; bestc = 2^log2c; bestg = 2^log2g;
end
end
end
%% 训练--
cmd = ['-c ', num2str(2^bestc), ' -g ', num2str(2^bestg) , ' -s 3 -p 0.4 -n 0.1'];
model = svmtrain(y,x,cmd);
% model
% 利用建立的模型看其在训练集合上的回归效果
% 注意libsvm3.2.0的svmpredict函数必须有三个参数输出
[py,~,~] = svmpredict(y,x,model);
figure;
plot(x,y,'o');
hold on;
plot(x,py,'g+');
%%
% 进行预测新的x值
%-- 产生[-1 1]的随机数
testx = -2+(2-(-2))*rand(10,1);
testy = zeros(10,1);% 理论y值无所谓
[ptesty,~,~] = svmpredict(testy,testx,model);
hold on;
plot(testx,ptesty,'r*');
legend('原始数据','回归数据','新数据');
grid on;
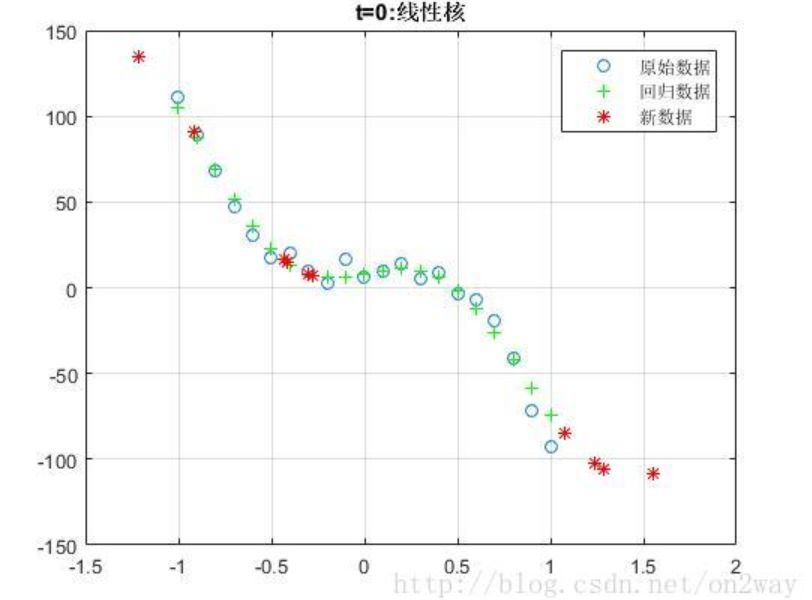
% title('t=0:线性核')
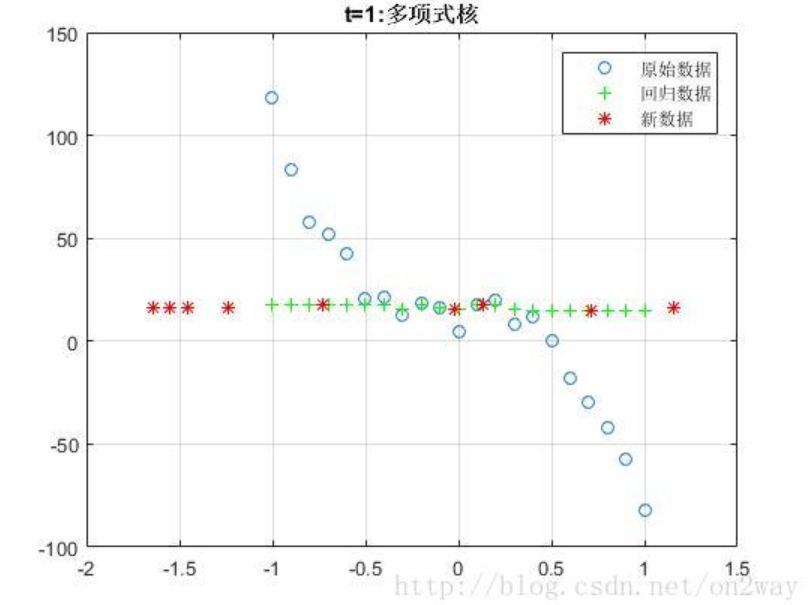
% title('t=1:多项式核')
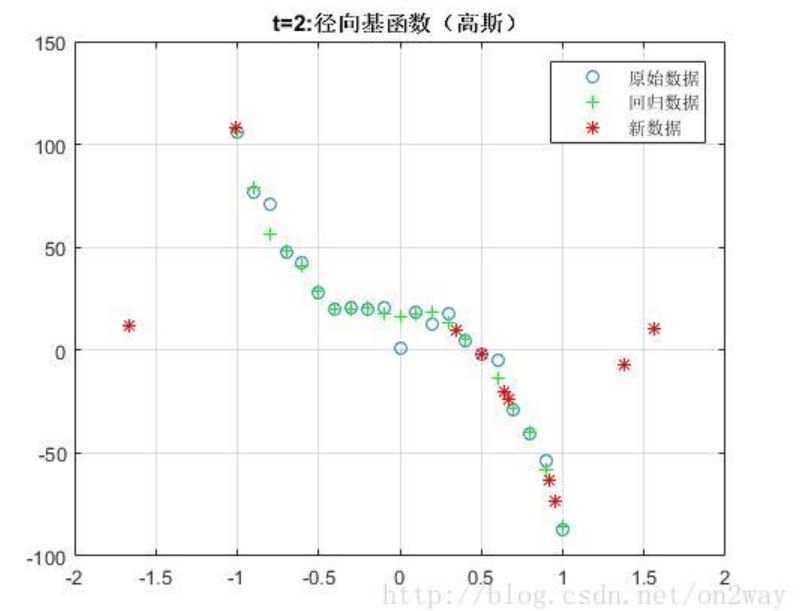
% title('t=2:径向基函数(高斯)')
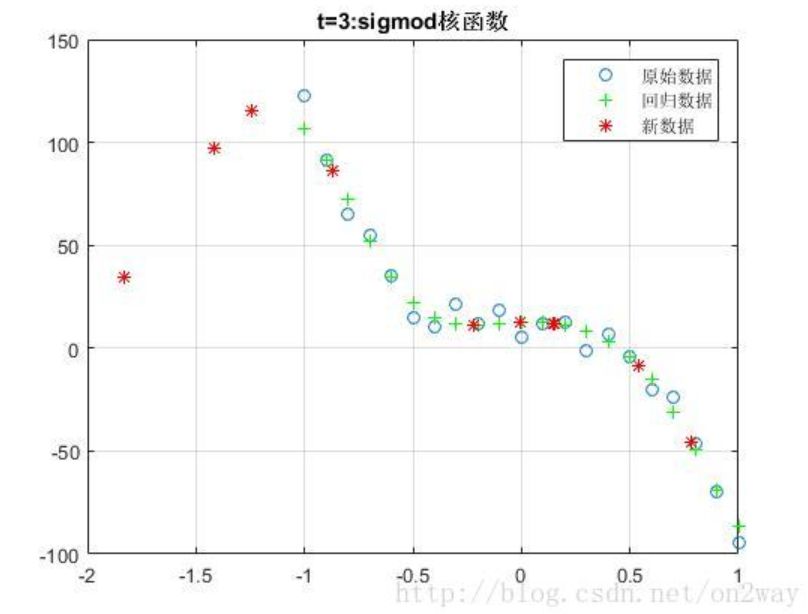
title('t=3:sigmod核函数')
这里我随机生成一个3次函数的随机数据,测试了几种不同svm里面的核函数:
因为我们的数据是由三次函数模拟生成的,所以可以看到,在这种情况下使用线性核t=0时候效果更好,然而实际情况下一般我们也不知道数据的分布函数,所以在选择核函数的时候还是需要多实验,找到最适合自己数据的核函数。
这里采用了交叉验证的方式自适应选择模型中重要的两个参数,需要注意的是参数的范围,不要太大,步长可能也需要控制,否则在数据量很大的时候需要运行很久。
至此SVM系列文章就到这里吧,感谢能看到这里的朋友~_~。
作者博客地址:https://blog.csdn.net/on2way