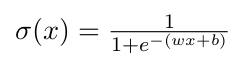神经网络如何完成表征？

本文为 AI 研习社编译的技术博客，原标题 ：

Representation Power of Neural Networks

作者 | ASHISH RANA

翻译 | 小冷、jinlilei   校对 | 酱番梨

整理 | 菠萝妹

原文链接：

https://towardsdatascience.com/representation-power-of-neural-networks-8e99a383586

注：本文的相关链接请点击文末【阅读原文】进行访问

我们了解神经网络以及它们从数据科学到计算机视觉的多个领域中的无数成就。众所周知，它们在解决有关泛化性方面的复杂任务中表现良好。从数学上讲，他们非常擅长近似任何的复杂函数。让我们形象化地理解这种近似概念，而不是前向和后向传播方法中的最小化预测误差。假设你了解前向和后向传播的一点基础，其旨在借助梯度和网络中的错误传播来近似函数。让我们通过另一种视觉解释来理解神经网络的近似能力。其中涉及基础数学和图形分析。 

在数学上，我们将研究给定神经网络的表征能力，以便提供近似的函数。

表征能力与神经网络的能力相关，神经网络会为特定实例分配适当标签并为该类创建明确定义的准确决策边界。在本文中，我们将探索一种视觉方法，用于更多地了解神经网络的近似特性，这与神经网络的表征能力直接相关。

  旅程

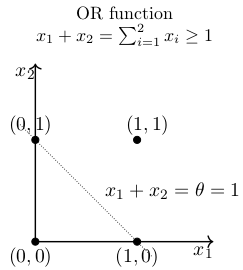
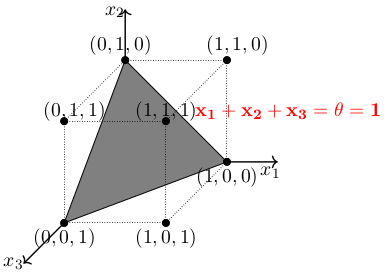
它始于MP 神经元模型，它是一个非常简化的神经元模型。通过非常简单地概念，神经元激活与否取决于某一阈值，即只有当其输入总和大于给定函数的阈值时，神经元才被激活，否则神经元不会发生输出信号。为了检查它的表征能力，让我们看它的几何解释。首先进行2-D分析，使用2个输入来近似OR函数，然后使用3个输入进行3-D分析。

对于二维坐标系中的分离，需要一条分类直线。神经元会向直线右侧的点发射信号。因此，就创建出了分离边界。 

对于三维坐标系中的分离，需要一个分类面。神经元会向这个面上方的所有的点发射信号。

因此，M-P神经元模型可用于表示任何线性可分的布尔函数。此外，我们可以看到一个严格的分界规则，而不是一个渐进的决策边界，任何略高于分离边界的为1，下面的正好为0。神经元触发了和阶梯函数一样的行为。感知器的每个输入都带有权重，但仍然存在严格的划分，从而实现了更大的灵活性。但是，上述机制不能处理非线性可分函数。一个非常简单的例子比如异或（XOR，两个输入如果相同，输出为0；两个输入如果是不同，输出为1），就无法用一条直线来分割开来，想象一下在这个函数的2维平面上绘制一条分离线。让感知器处理异或这样线性不可分问题，它就无能为力了。大多数数据与异或非常相似，本质上是线性不可分的。

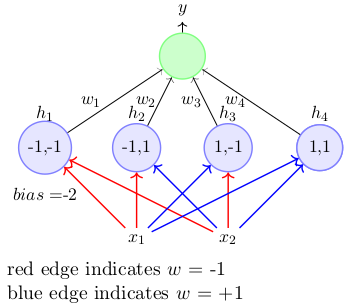
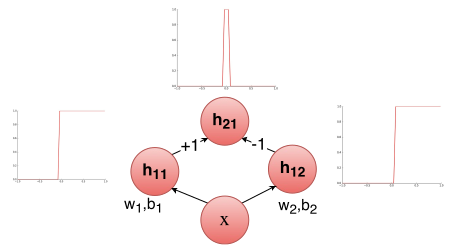
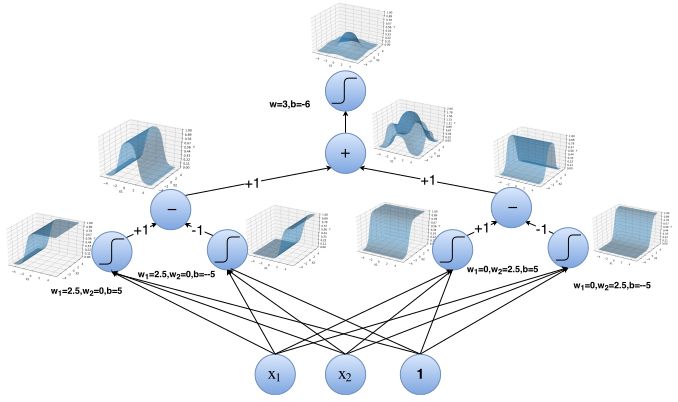
因此，需要先进的计算模型，如当前需要为这些函数创建分离边界的神经网络。只需看一个包含一个隐藏层和一些复制异或函数的预定义权重的基本图。

图：红线表示权重为-1，蓝色表示权重为+1

异或函数实现的条件：w1 <w0，w2≥w0，w3≥w0，w4 <w0

记住：具有n个输入的任何布尔函数都可以由感知器网络表示，感知器网络包含具有2 ^ n个感知器的1个隐藏层和包含1个感知器的1个输出层。这是充分不必要条件。

通过我们对具有阶梯函数（如近似）的单个隐藏层网络的分析。它的严格判断标准与阶梯函数一样具有局限性。让我们深入研究具有S形非线性逼近函数的多层深度网络。

  时过境迁

经过sigmoid激活的神经元具有非常强的表征能力。具有一个单隐层的多层神经元网络可以近似任意连续函数，并达到任何想达到的精度。

数学上，可以得到这样的证明：对于任意函数f(x):R(n)→ R(m)，我们总可以找到一个拥有(单或多)隐层的神经网络，其输出g(x)满足 |g(x)-f(x)| < Θ.

上述的说法在自然界中是非常的。因为它意味着，我们可以用一个给定的神经网络去近似任意函数。从数学角度来讲，万能近似定理(universal approximation theorem)指出，在对激活函数温和的假设下，一个包含有限神经元的单隐层自编码网络可以近似R(n)紧致子集上的任意连续函数。这个理论因此也就说明，在给定合适参数下，简单的神经网络可以代表各种各样的函数。然而，它并没有涉及到那些参数的算法收敛性。收敛是和前馈、后馈算法相关的。下面让我们通过一种直观的解释方式来理解上述理论，它是神经网络学习的基础。 

对函数近似的几何解释。是数值近似中一种经典的数学方式。

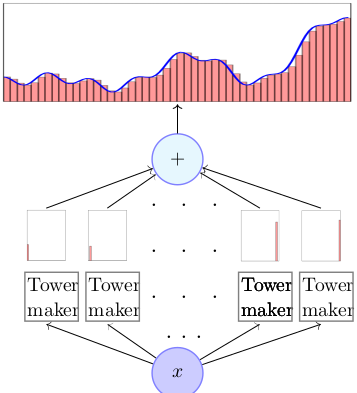
  结束游戏：Sigmoids的塔

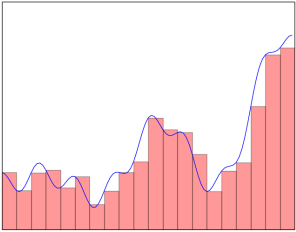
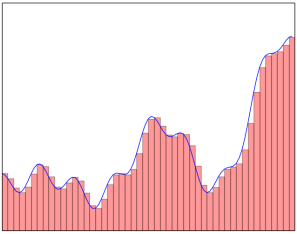
继续上述与神经网络近似函数的对话。只需看下面的图表并自行决定。可以通过叠加多个塔功能来近似函数。该过程将形成与给定函数等效的形状，其中与一些小的近似误差是近似的。现在，上面对通用近似定理的解释告诉我们，我们用于近似的更多塔数是近似行为。因此，调整在Sigmoid激活函数中参数，目的是创建这样的近似塔。从理论上讲，根据这种解释，对神经网络的准确性没有限制。 

显然，塔的数量越多，近似效果越好，近似误差越小。

让我们更深入地探讨这个解释过程。所有这些“tower”功能都是相似的，只是它们在x轴上的高度和位置不同。现在，我们必须看看这些Towers是如何用sigmoid激活函数创建的。

我们的目标是找出用于塔式结构的黑匣子塔式制造机。

典型的逻辑sigmoid激活函数方程如下。

w：代表权重 b：代表偏置

随着w的增加，函数变得像阶梯函数更陡峭。b的更正值将曲线从原始曲线向左移动。 

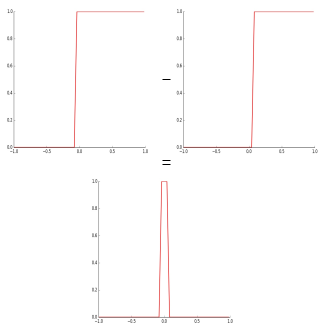
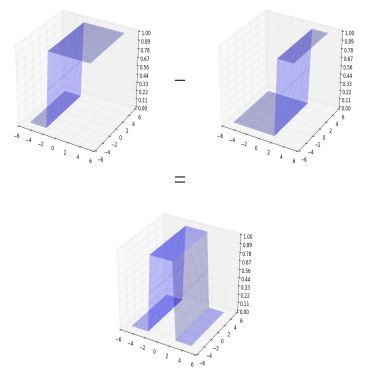
因此，通过改变这些值，我们可以创建不同版本的sigmoids激活函数，我们可以相互叠加以获得塔状结构。为了在二维坐标系中创建塔，减去两个曲线不同的偏置值。 

左曲线的偏置值b具有更大的正值。因此，上面的随机曲线可以用多个这样的塔近似或表示。

我们可以将此操作扩展到神经网络的隐藏层，以构建模拟这种曲线减法方法的神经网络。因此，神经网络可以表示任何具有权重和偏置的参数值的这样的函数，我们使用我们的前向和后向传播算法不断的确定这些参数值直到收敛标准。

现在，可以通过叠加这样的塔来近似上述功能的随机曲线。 

  案例研究

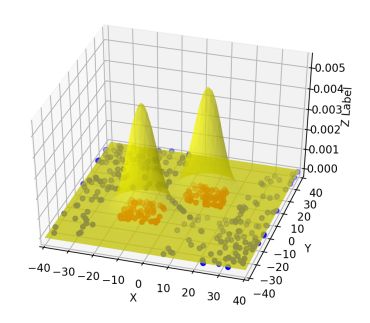
考虑具有多个输入的场景。假设我们在海床的特定位置是否会找到石油这个问题试图做出决策。此外，假设我们的决策基于两个因素：盐度（x1）和压力（x2）。一些数据已经给了我们， y(有油|无油) 似乎是一个x1和x2的复合函数。我们想要一个神经网络来近似这个函数。 

上面的插图绘制了上述场景。显然，我们需要三维塔近似这个分布函数。

按照我们的理解，需要在三维坐标系中制作这样的三维闭合塔。如果我们继续使用上述类似的方法，在三维空间中，两个有不同偏置值的sigmoids激活函数相减。我们将得到以下的等效曲线。

我们仍然没有得到一个封闭的塔。

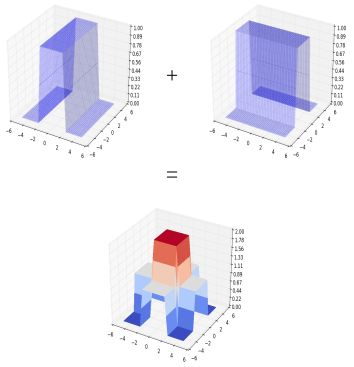
但是，我们可以看到，如果我们采用另一个水平垂直的塔架到现在组合的曲线上。在叠加这两个水平垂直的开放式塔时，我们就可以得到封闭的塔。

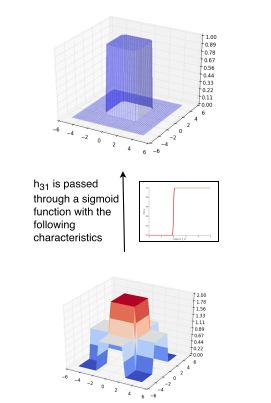
我们可以通过另一个组合的sigmoid激活函数来传递上面的输出， 从而能得到一个最近似的合适的塔。 

我们现在可以通过总结许多这样的塔来近似任何的函数。

上述案例研究中的复杂分布函数可以借助多个这样的塔来重建。在这里，我们看一个神经网络来表示上述过程。

我们可以通过另一个组合的sigmoid激活函数来传递上面的输出， 这意味着我们可以有一个神经网络，它可以准确地分离出像上面的案例研究中提到的分布。对神经网络的准确性没有理论上的限制。 

我们有兴趣将蓝点与红点分开。单个S形神经元存在明显的误差。但是，通过两个隐藏层，我们可以通过塔的总和来近似上述函数。我们可以有一个神经网络，它可以准确地将蓝点与红点分开！

  致谢

用于近似的可视化方法非常独特而且有趣，这就是我觉得需要进行这次讨论的原因。我只是重新构建了来自neuralnetworksanddeeplearning.com的现有解释。描述性插图来自深度学习课程CS7015。感谢Mitesh M. Khapra教授和他的助教提供了这门精彩的课程！

想要继续查看该篇文章相关链接和参考文献？

长按链接点击打开或点击底部【阅读原文】：

http://ai.yanxishe.com/page/TextTranslation/1210

AI研习社每日更新精彩内容，观看更多精彩内容：

进入 kaggle 竞赛前 2% 的秘诀

如何极大效率地提高你训练模型的速度？

用 4 种卷积神经网络，轻松分类时尚图像

这 25 个开源机器学习项目，一般人我不告诉 Ta

等你来译：

2018.11十大机器学习热门网文

循环神经网络的 Python 案例

时序预测的贝叶斯方法

一文带你读懂 WaveNet：谷歌助手的声音合成器