【剑桥大学ICLR2020】卷积条件神经过程，Convolutional Conditional Neural Processes

简介：

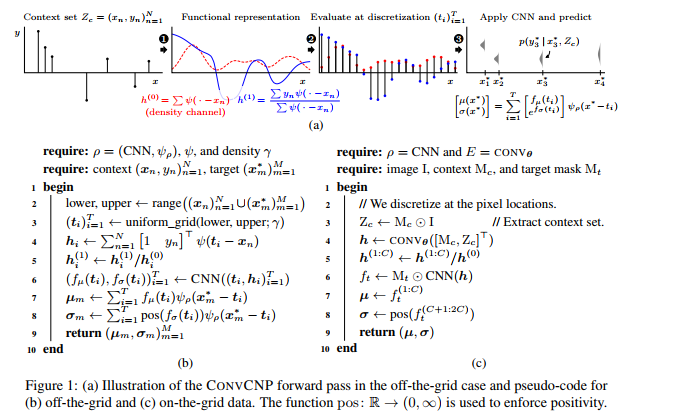
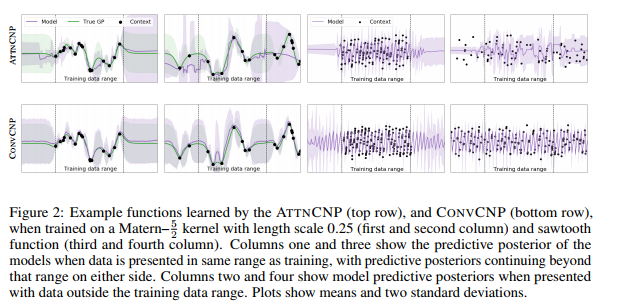
我们介绍了卷积条件神经过程（CONVCNP），它是对数据中的翻译等方性进行建模的神经过程家族的新成员。 翻译等方差是许多学习问题的重要归纳偏差，包括时间序列建模，空间数据和图像。 该模型将数据集嵌入到无穷维函数空间中，而不是无穷维向量空间中。 为了使这一概念正式化，我们将集合的神经表示的理论扩展到包括功能表示，并证明可以使用卷积深度集来表示任何平移等价嵌入。 我们在几种设置下评估CONVCNP，表明与现有NP相比，它们具有最先进的性能。 我们证明，通过构建翻译等方差，可以对挑战性的域外任务进行零镜头概括。