视频 |【古希腊的数学与天文学】- 希腊罗马文明讲座

俞磊老师所讲的希腊罗马文明讲座, 非常精彩, 这里分享大家. 已获俞老师授权发布, 特此感谢!  俞老师个人网站: https://home.yulei.org 

此希腊罗马文明讲座从古希腊神话讲起，依次对古希腊文明的兴起、希腊城邦制度、希腊的数学和天文学成就、从科林斯战争到马其顿的征服、直至西罗马灭亡的发展演进历程. 

其中数学和天文学两部分视频直接可在此文中观看, 另有 [遇见数学] 制作部分动图在内, 讲座其余视频可在文末链接中查看. 

12 古希腊的数学

点击边框调出视频工具条

希腊化时代的科学

• 希腊科学是希腊自然哲学进一步发展的结果

• 演绎推理及实证体系是人类其他文明所没有的

• 近代科学不可能从其他文明中产生
  

• 希腊化时代是人类第一次真正意义上的科学时代

• 近代科学是希腊化时代科学的延续

• 多数希腊科学的著作均已失传
  

科学研究之目的

• "从就我们来说明白和易知的东西进到就自然来说明白和易知的东西. "

  - 亚里士多德《物理学》

早期毕氏学派对数学的贡献

• 数学原理为世界之本源

• 数字与几何学

• 毕达哥拉斯定理的证明

• 无理数的发现

• 证明可以观看此视频【希帕索斯之死 - 如何理解无理数】
  

三个数学问题

• 三等分角、化圆为方、倍立方

希庇亚斯(约公元前 460 年)

• 使用割圆曲线, 解决任意等分角的问题

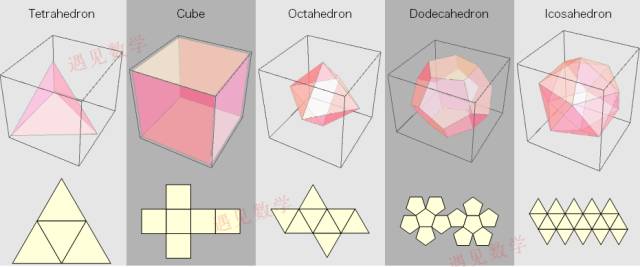
柏拉图正多面体

• 只有 5 种正多面体

• 正四面体(火)

• 正立方体(土)

• 正八面体(气)

• 正十二面体(神?)

• 正二十面体(水)

欧几里得(约公元前 325 年 ~ 前 265 年)

• 《几何原本》一书

• 定义、公理、定理的体系

• 5 个公理, 5 个公设, 23 个定义和 467 个命题

• 五个公理: 

• 两点之间可以做一条直线

• 直线两边可以任意延长

• 可以作一圆, 具有指定的圆心和指定的半径

• 所有的直角都相等

• 平行公理: 给定一条直线, 通过此直线外的任意一点, 有且只有一条直线与之平行

• 徐光启于明朝末年翻译《几何原本》

• 《光学》一书

• 触须假说(光的感觉是人眼中伸出的触须的感觉)

• 光的折射、反射

• 球面光学
  

阿波罗尼奥斯(约前 262 年 ~前 190 年)

• 地心说 - 提出本轮模型

• 圆锥曲线 - 在西方又叫做阿波罗尼奥斯曲线

• 《圆锥曲线》一书, 共证明了关于圆锥曲线的 487 个定理
  

• 《论蜗线》一书

• 讲述圆柱螺旋线的理论

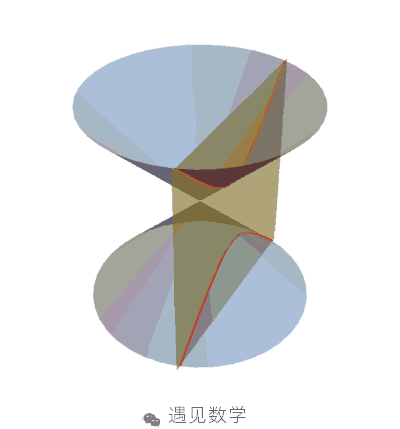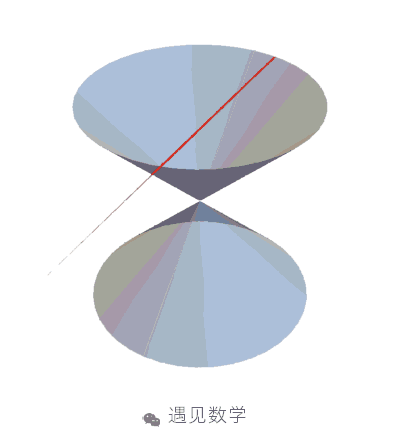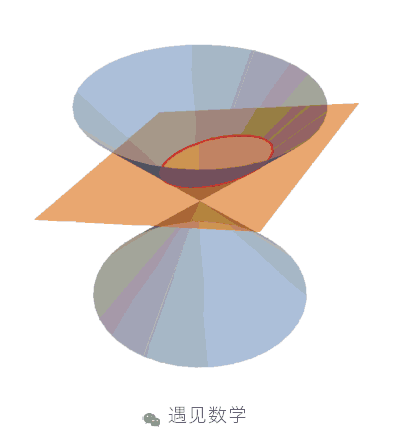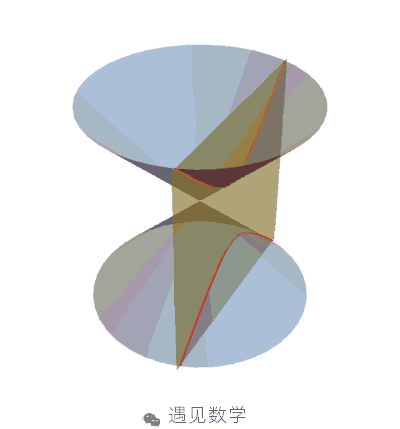
阿基米德(前 287 年 ~ 前 212 年)

• 《浮体》

• 定义液体是各个部分之间摩擦力为 0 的物体

• 由此证明了著名的阿基米德定律

• 《平面平衡》

• 关于静力学的 15 个命题的证明(包括杠杆原理)

• 《抛物线求积》

• 证明了抛物线弓形的面积是其同底同高的三角形面积的三分之四

• 《球和圆柱》, 《圆的度量》, 《论螺线》, 《劈锥曲线和椭球体》等等

阿基米德成就

• 球的表面积是其内接最大圆面积的四倍

• 圆柱内切球体的体积是圆柱体积的2/3

• 此定理后来刻在阿基米德的墓碑上
  

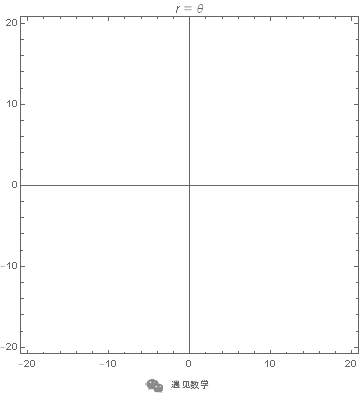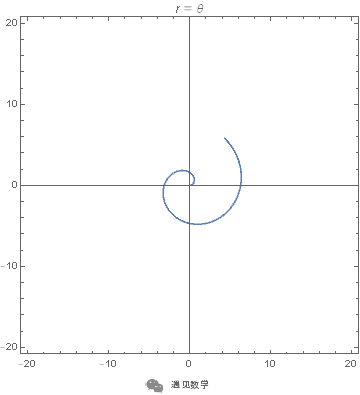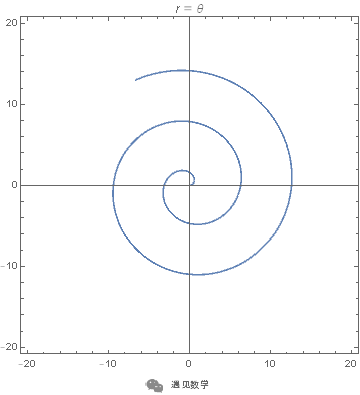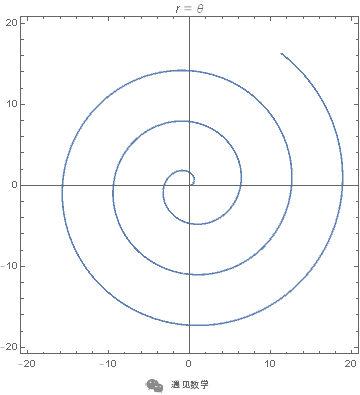
• 阿基米德螺线 - 等速螺线

丢番图(约前 298 年 ~ 前 214 年)

• 代数学之父

• 《算数》一书

• 整系数多项式方程 - 西方又称丢番图方程

丢番图的墓志铭

这个墓裡长眠着丢番图。

啊！多么伟大的人呀！

上帝给予的童年占六分之一，

又过十二分之一，两颊长鬍，

再过七分之一，完成终身大事。

五年后天赐贵子，可怜迟到的宁馨儿，

享年仅及其父之半，便进入冰冷的墓，

在充满悲伤的四年后，他也走完了人生的旅途. 

丢番图与费马大定理

• 1637 年, 费马在阅读丢番图的《算数》时在第 11 卷第 8 命题时, 在一旁写道: 

• 将一个立方数分成两个立方数之和，或一个四次幂分成两个四次幂之和，或者一般地将一个高于二次的幂分成两个同次幂之和，这是不可能的。关于此，我确信我发现了一种美妙的证法，可惜这里的空白处太小，写不下. 

13 古希腊的天文学

点击边框调出视频工具条

希腊罗马文明系列讲座

01 希腊神话（上）

02 希腊神话（下）　

03 爱琴海文明，希腊文明兴起，古代奥运会，希腊自然哲学

04 希腊城邦制度

05 古希腊的悲剧和喜剧 希腊波斯战争

06 伯里克利时代 

07 伯罗奔尼撒战争

08 苏格拉底、色诺芬、柏拉图

09 从科林斯战争到马其顿征服

10 亚里士多德和亚历山大

11 继业者战争

12 古希腊的数学

13 古希腊的天文学

14 罗马和意大利的早期历史

15 罗马共和国（上） 从早期到布匿战争

16 罗马共和国（下） 罗马内战

17 罗马早期帝国

18 后期希腊哲学 三世纪危机

19 后期希腊哲学 三世纪危机

20 民族大迁徙和西罗马的灭亡

21 结束语，西罗马灭亡后的西方

更多精彩讲座视频可移步到俞磊老师网站观看.