蒙特卡洛与赌博模型

蒙特卡洛_赌博模型

来，先谈一部电影！

《决胜21点》讲述了几位数学天才少年凭才智大闹赌城拉斯维加斯的故事。举世闻名的麻省理工，堪称是莘莘学子、科学天才们向往的圣地。作为有幸能到这里读书的新生，本·坎贝尔（吉姆·斯特吉斯饰）自然也有他的过人之处。的确，坎贝尔超常的数学运算才能在他进入麻省理工没多久就开始崭露头角。学院里讲授数学理论课程的米基·罗萨（凯文·史派西饰）更是一眼就看中了小伙子，并对其光明的未来充满了信心。经过短暂的接触之后，罗萨教授将这位数学天才介绍给他精心培养的另外几位数学高才生认识，并邀其加入一个由罗萨领导，由吉尔（凯特·波茨沃斯饰）、费舍（雅各布·皮特斯饰）等数学天才共同组成的“特殊团队”，专攻赌场上风行的“21点”游戏。运用他们对于数学的尖端认识和运算，在经验丰富的罗萨教授的指导下，轻松应对“21点”游戏中可能出现的各种局面，最终确保高频率地取胜纪录。

诶？听上去貌似都有点道理！您觉得呢？手指继续动，跟我继续看下去……

 下面我开始数学建模，然后用蒙特卡洛模拟历史上最常见的几种赌博模型。

 

一 symplebedding system

数学天才可以在赌场春风得意，但普通人没这么好运气。因为第一赌场要抽成，首先让你不利，在大数定理面前，赌博次数越多，输钱概率就越大。所以赌场安排好了规则后，通常只做一件事，就是让你不停赌博。只要堵得次数越多，大数定理对你越不利。况且赌场指定规则并非5:5平等，赌客赢钱概率不到50%，不利因素还不止一个。

下面我用Python建立蒙特卡洛模型，模拟大数定理（赌博次数越多，输钱概率就越大）

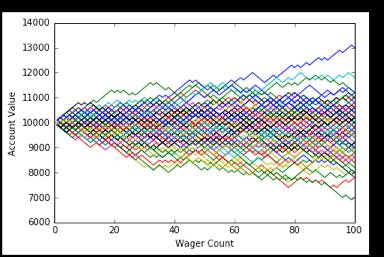
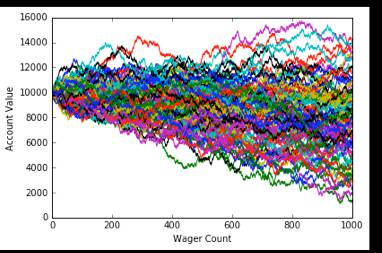
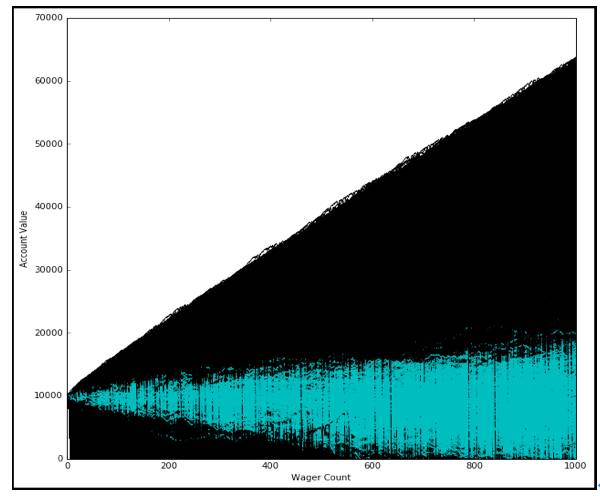
纵坐标表示手里赌博金额，横坐标是赌博次数

起始赌金10000元，这里有一百条曲线，代表一百个赌徒，赌博次数为100次时，大概有50条曲线在10000元以上，50条曲线在10000元以下。这表示赢钱和输钱的人差不多。

仍然一百个赌徒，赌博次数增加到一千次，大多数曲线走势低于10000元，表示破产的人多于赢钱的人。赌博次数少时，大数定理不明显。赌博次数多时大数定理开始发挥作用。
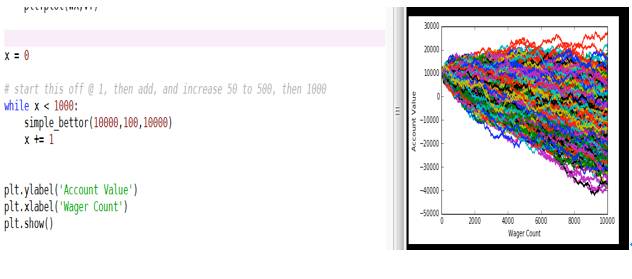
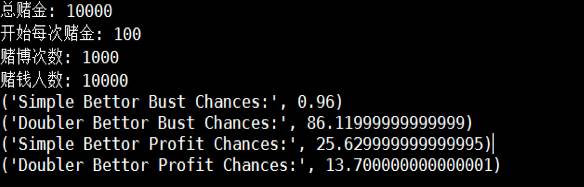
simple_bettor(10000,100,1000)

随着赌博次数增加到一万次，赌博人数达到一千人，可以看到大数法则体现，绝大多数人都破产。

 

二 doublebedding system

伏尔泰的情妇，夏特莱侯爵夫人是个数学家和物理学家。夏特莱出身贵族，受过良好的教育。1733年以后，她同当时杰出的学者伏尔泰*建立了联系。她又是牟培尔堆*的亲密朋友之一。当时赌博在欧洲盛行，贵族也不例外。伯爵夫人提出了double bedding system，即双倍法，这次输了，下次赌注加一倍，如果赢了就可以把上次输的钱捞回来。不幸的是夏特莱侯爵夫人的双倍法输光了所有钱，发生了著名的与伏尔泰私奔事件。

（Chatelet, Gabrielle-Emilie Le Tonnelier de Breteuil,Marchioness du）

我用蒙特卡洛模拟后，发现伯爵夫的双倍法破产，破产率很高，赢钱率也不如simple。

三 D'AlembertStrategy

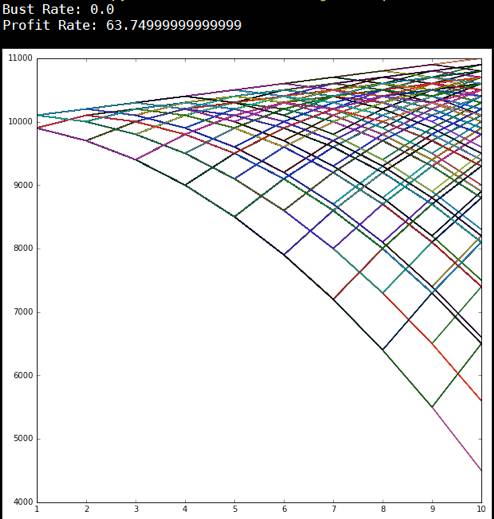
达朗贝尔（1717～1783）法国著名的物理学家、数学家和天文学家。1717年11月17日生于巴黎，1783年10月29日卒于巴黎。一生研究了大量课题，完成了涉及多个科学领域的论文和专著，其中最著名的有八卷巨著《数学手册》、力学专著《动力学》、23卷的《文集》、《百科全书》的序言等等。他提出的达朗贝尔赌博模型比较保守，不容易输钱，不会像夏特莱侯爵夫人把大量钱输的精光。

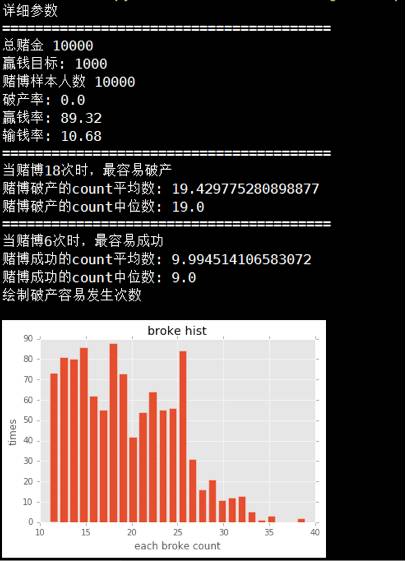
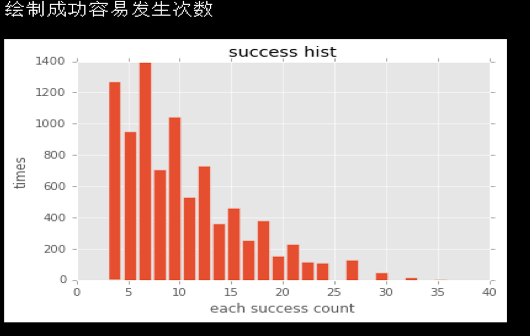
经过模特卡洛模拟发现
优点：破产率几乎为0
缺点：赢钱率不高，64%左右，赢的钱不多，做多10%左右

 

四 LabouchereSystem

那么，我们能找到一个优秀赌博算法模型嘛，能赢很多钱，赢得概率又大？答案是有的，看了皇家赌场007电影知道，英国政府机构派007詹姆士邦德去赢恐怖分子的钱。英国政府可不愿意输钱，他们为007定制了一套高胜率的算法，数学上成为Labouchere System。

 

此算法能有90%胜率，其原因：
1.目标明确，减少多余风险
2.吸收 D'Alembert算法优点，减少倍数带来巨大波动风险
3.分治算法，把目标分成几等分，逐步实现
4.总赌金和目标比值10:1合理，能有足够赌金和时间空间去赢钱或达到目的

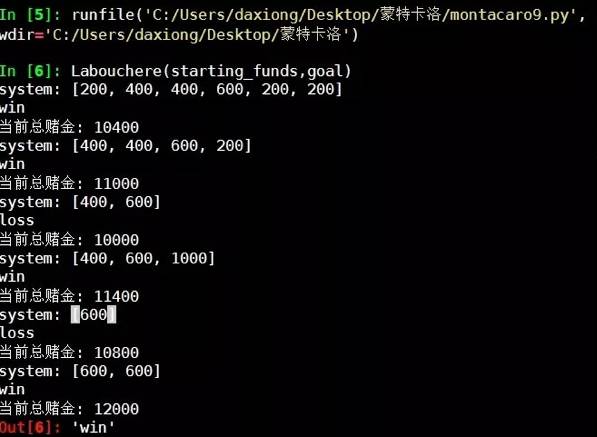
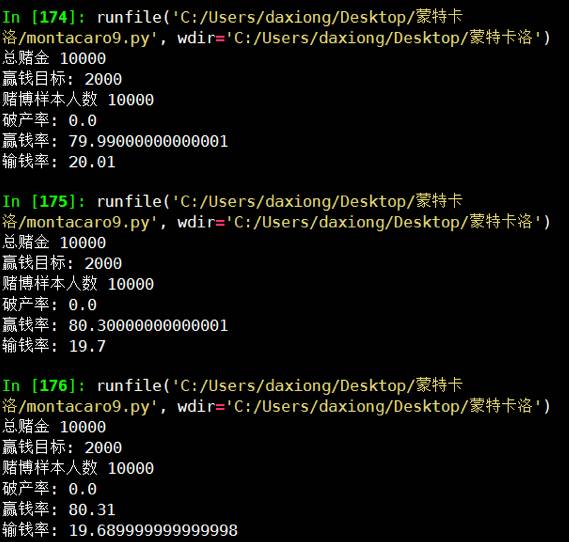
单次Labouchere模拟Labouchere System for Gambling Tested

总赌金和赢取目标金额比例是1/10，胜率就有百分之90

总结，今天我用蒙特卡洛模拟了历史上常见几种赌博模型，由于专业性较强，赌博模型只是简单介绍，以后有机会可详细阐述。

在真实的赌场上，赌客持久赢钱概率很低。

现在赌场都是高科技行业，拥有较多数学工程师和计算机工程师，赌客无时无刻都被赌场设计的模型算计。

因此去赌场寻欢作乐还行，赢小钱还可以，想赢很多钱，嗯，看你运气了，

---

☞  哈尔莫斯：怎样做数学研究

☞  扎克伯格2017年哈佛大学毕业演讲

☞  线性代数在组合数学中的应用

☞  你见过真的菲利普曲线吗？

☞  支持向量机(SVM)的故事是这样子的

☞  深度神经网络中的数学，对你来说会不会太难？

☞  编程需要知道多少数学知识？

☞  陈省身——什么是几何学

☞  模式识别研究的回顾与展望

☞  曲面论

☞  曲面论（第二讲）

☞  自然底数e的意义是什么？

☞  如何向5岁小孩解释什么是支持向量机（SVM）？

☞  华裔天才数学家陶哲轩自述

☞  代数，分析，几何与拓扑，现代数学的三大方法论

算法数学之美微信公众号欢迎赐稿

稿件涉及数学、物理、算法、计算机、编程等相关领域。

稿件一经采用，我们将奉上稿酬。

投稿邮箱：math_alg@163.com