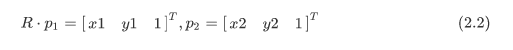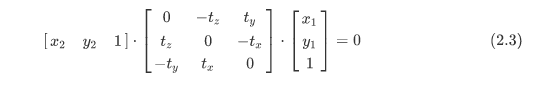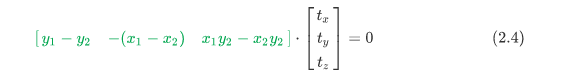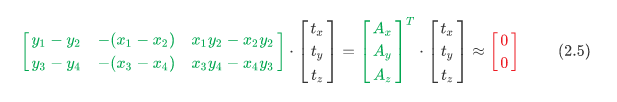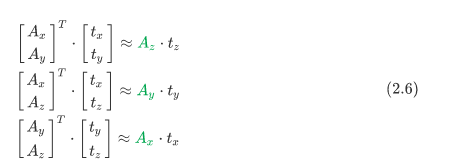【泡泡读者来稿】一步步深入了解S-MSCKF（一）

2018 年 10 月 24 日 泡泡机器人SLAM

0.前言

0.1 我为什么写这个?

　　一方面是对自己看过的东西做一个简单的总结,之前也看过一些其他的,但都没有系统的成文,因为时间比较紧张, 科研压力比较大.另外一方面是向各位大佬们学习,希望能得到大佬们的指导, 同时希望对刚入门SLAM和已经入门一段时间的SLAM小伙伴一点干货. 结交一些志同道合的小伙伴!

0.2 可爱的您能得到什么?

　　如果您正在研究MSCKF或者对VIO很感兴趣,那么您将得到以下几件东西:

(1) 一份看了不会亏的MSCKF的入门指南

(2) 基本我自己推导过的一本书(或者叫比较长的论文) Quaternion kinematics for the error-state Kalman filter

(3) 一份注释过的开源版本的代码

　　如果您是已经最MSCKF及其熟悉的大佬,那么您将得到:

其实我也还没想好您能得到什么,我倒是很想从您那得到一些东西...

0.3 我希望可爱的您反馈什么?

(1) 全文一些描述有误的地方,因为自己写东西比较随意,难免有大家理解起来有问题或者本身就描述不对的地方.

(2) 反馈网址戳这里, 可爱的您一定会随手在github留下小星星对不对? 不方便公共留言的话可以邮箱私聊我.

(3) 交个朋友? 江湖有缘相见. 祝可爱的您科研顺利,一夜暴富!!!

1.简介

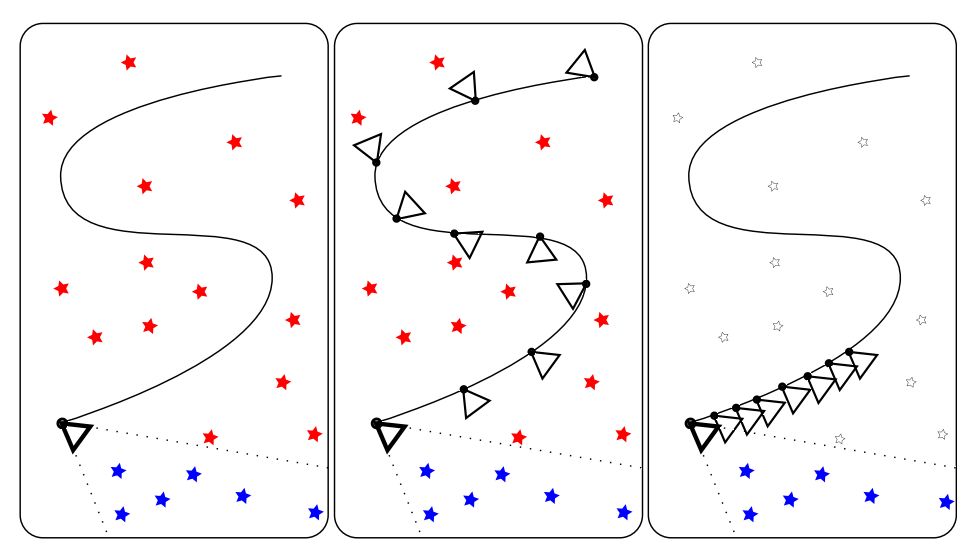
　　MSCKF (Multi-State Constraint Kalman Filter),从2007年提出至今,一直是filter-based SLAM比较经典的实现.据说这也是谷歌tango里面的算法，这要感谢Mingyang Li博士在MSCKF的不懈工作。在传统的EKF-SLAM框架中，特征点的信息会加入到特征向量和协方差矩阵里,这种方法的缺点是特征点的信息会给一个初始深度和初始协方差，如果不正确的话，极容易导致后面不收敛，出现inconsistent的情况。MSCKF维护一个pose的FIFO，按照时间顺序排列，可以称为滑动窗口，一个特征点在滑动窗口的几个位姿都被观察到的话，就会在这几个位姿间建立约束，从而进行KF的更新。如下图所示, 左边代表的是传统EKF SLAM, 红色五角星是old feature,这个也是保存在状态向量中的,另外状态向量中只保存最新的相机姿态; 中间这张可以表示的是keyframe-based SLAM, 它会保存稀疏的关键帧和它们之间相关联的地图点; 最右边这张则可以代表MSCKF的一个基本结构, MSCKF中老的地图点和滑窗之外的相机姿态是被丢弃的, 它只存了滑窗内部的相机姿态和它们共享的地图点.

符号说明

2.前端

　　本文主要针对2017年Kumar实验室开源的S-MSCKF进行详细分析,其实这篇文章整体思路与07年提出的基本上是一脉相承的.作为一个VIO的前端,MSCKF采用的是光流跟踪特征点的方法,特征点使用的是FAST特征,另外这是MSCKF双目的一个实现,双目之间的特征点匹配采用的也是光流,这与传统的基于descriptor匹配的方法不同.前端部分其实相对简单,整个前端部分基本在 image_processor.cpp中实现.

2.1 基本数据结构说明

A.特征点检测和跟踪的参数

B. 特征点数据

2.2 跟踪流程

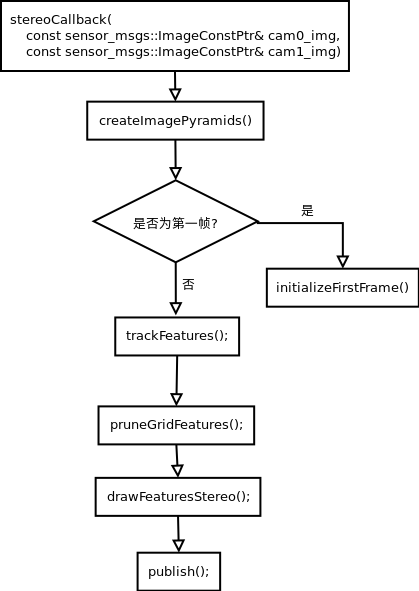
　　整体框架如下面的流程图所示:

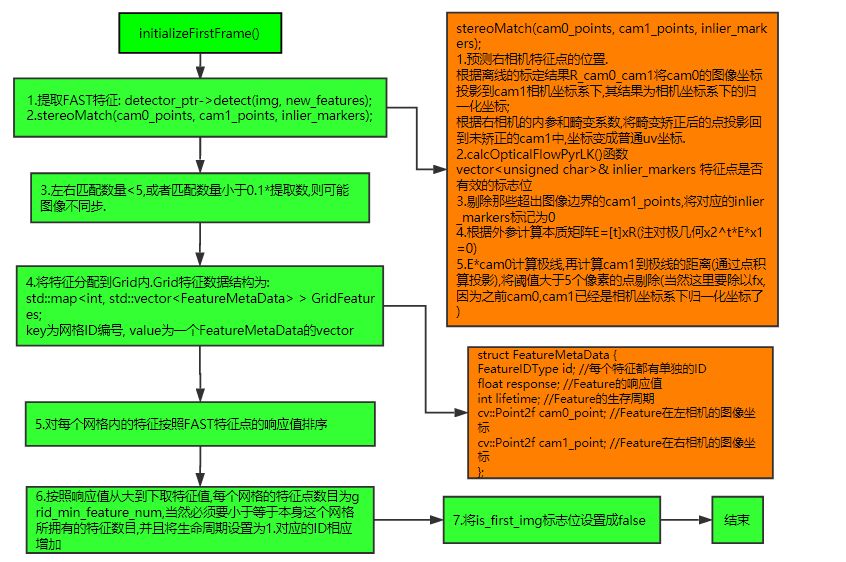
2.2.1 Initialization

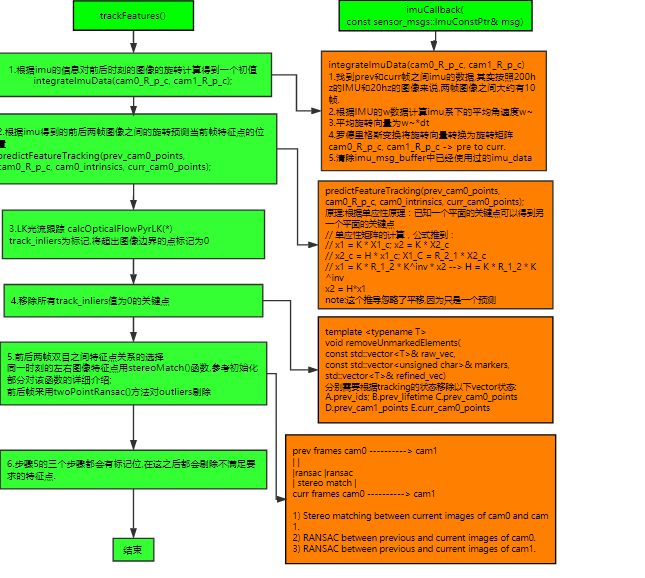
2.2.2 trackFeatures

　　当第一帧初始化完成之后,后面帧则只需要进行跟踪第一帧的特征点,并且提取新的特征点,整个流程如下:

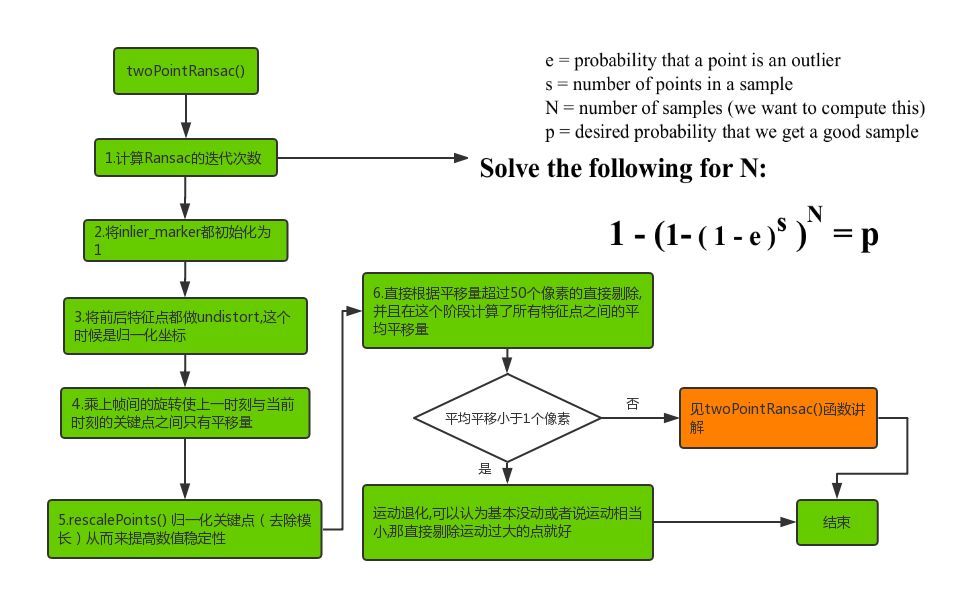
整个流程还算比较清晰,但是有一个步骤需要单独说明一下,也就是作者在论文中提到的twoPointRansac的方法.我们先来看一下函数原型:

整个函数的基本流程如下:

下面我们来详细讲解一下RANSAC模型及原理依据: 我们由对极几何可以知道有以下约束:

我们假设前后帧对应点归一化坐标分别为,

其中R为根据IMU的平均角速度得到的,此时坐标系都统一到一个坐标系下.

将式子(2.3)展开之后我们可以得到:

其中绿色部分在代码中对应这一块:

至于这个模型是怎么选出来的呢? 假设一共有N个inliers点对,那么根据式(2.4)势必会得到一个N*3 * 3*1 = N(0)的等式.但事实上由于误差和outliers的存在,最终结果不可能为零,我们取两个点将式子分块,并且只考虑两个点的情况,那么将会有:

那我们可以分别得到以下三个式子:

我们的目标当然是使得误差最小,所以作者的做法是比较式子(2.6)绿色部分的大小,取最小的并令模型的平移为1,进而直接求逆然后得到最初的模型假设,之后要做的步骤跟常规RANSAC就十分接近了,找出适应当前模型的所有inliers,然后计算误差并不断迭代找到最好的模型. 　　至此我们已经完成了整个feature的tracking过程!

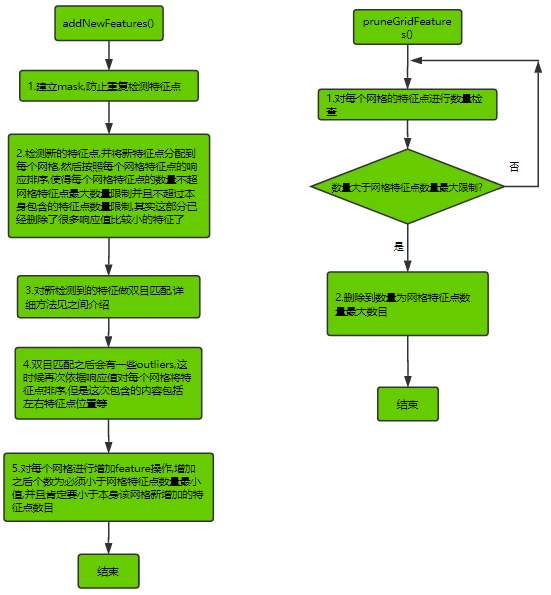
2.2.3 addNewFeatures & pruneGridFeatures

　　如果一直tracking的话那么随着时间流逝,有些特征会消失,有些可能也会有累计误差,所以我们势必要添加一些新的特征,这个步骤正是在跟踪上一帧特征之后要做的,因为stereoMatching 和twoPointRansac都会剔除一些outliers,那我们需要提取新的特征保证能一直运行下去.

2.2.4 publish

　　主要发布了当前帧特征点的数据,每个特征的数据结构为FeasureMeasurement如下:

发布的其实是CameraMeasurement,那其实就是一个包含上面特征数据FeasureMeasurement的一个数组.

2.3 显示

其实前端基本上可以说是非常简单了,也没有太多的trick,最后我们来看一下前端的跟踪效果的动图:

3.基于四元数的 error-state Kalman Filter

其实原理部分相当重要,包括你对error-state Kalman Filter的理解,但是如果要从头讲起的话可以说篇幅太长,考虑到做SLAM的同学们基本上都应该知道这本书 Quaternion kinematics for the error-state Kalman filter, 这本书会让你在四元数,SO3,IMU的模型以及基于IMU的ESKF(error-state Kalman Filter)都会有比较深刻的理解,对应这本书我也做了很多注释,关于基于四元数原理部分由于篇幅限制,我这里不想做太多的说明,但是接下来在讲解S-MSCKF原理部分我们会将参考公式附上.下面是一些我在这本参考资料中的注释图.

当然重要的事情需要说三遍,那就是Quaternion kinematics for the error-state Kalman filter四元数是Hamilton表示方法,而MSCKF中采用的是JPL表示方法,关于这两者的不同,可以参考书中34页,Table2.

　　看过论文代码的同学可能会说,MSCKF这一部分代码参考的是MARS实验室Indirect Kalman Filter for 3D Attitude Estimation-A Tutorial for Quaternion Algebra,答案是肯定的.但是我的建议是以Hamilton那本书为基础,然后自行再去推导MARS出品那一本,那样你的体验会更加深刻.

未完待续。。。。