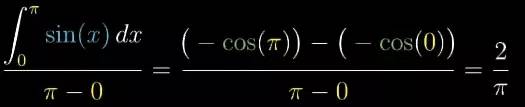来自 3Blue1Brown 《微积分的本质》视频: https://space.bilibili.com/88461692
(点击最下阅读原文查看B站更多精彩内容) 这里特别感谢各位翻译的贡献:昨梦电羊,罗兹,Solara570,圆桌字幕组等。 有意的译者请移步B站进行联系!
[遇见数学]根据视频内容整理文字版, 方便各位同学学习, 先来看下视频吧.
正文
![]()
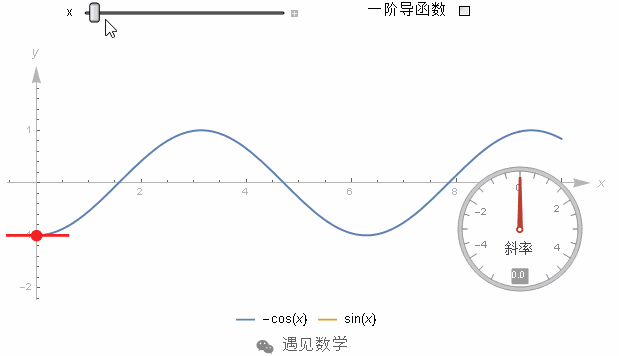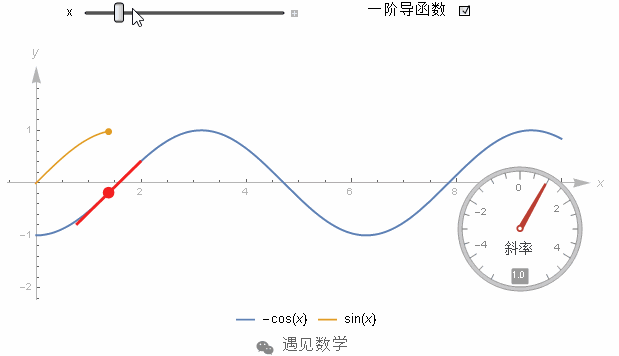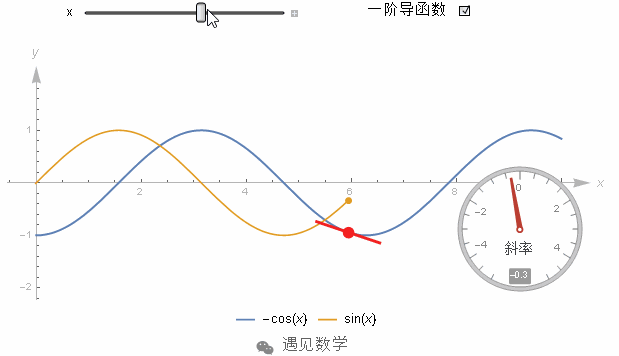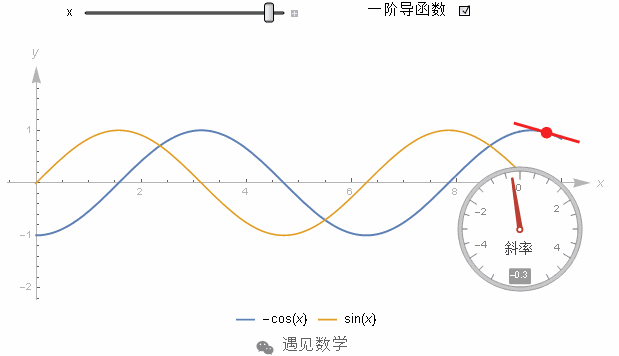
今天我想要讨论一类要用到积分的常见问题:求一个连续变量的平均值. 这类问题本身就具有实际用途, 而且也从另一个不同的视角告诉我们, 为什么积分和求导是互逆的一种运算?让我们以 sin(x) 在 0 到 π 之间的半个周期为例.
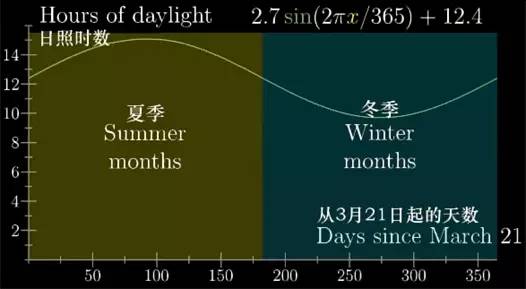
请问在这个区间内图像的平均高度是多少?这不是一个没有意义的问题。世界上种种周期现象都可以用正弦曲线来描述. 比如每天的日照时间, 就是一个对应着日期的正弦函数(请查看《吃了冬至饭一天长一线》).
所以如果你想要预测太阳能电池板在夏天和冬天的平均效率的差别, 那么,你就需要回答如下问题. 正弦函数在半个周期上的平均值是多少?
![]()
在上述现实的例子中,各种系数和常数会让情况更加复杂. 所以我们仅先关注单纯的正弦函数, 不过计算的方法在其他情况中都是一样的.
![]()
一个连续变量的平均值,这听起来有点奇怪. 通常在提到平均值的概念时, 我们首先想到的是有限个变量, 用其总和除以数量的方法得到均值.
但是 sin(x) 在 0 到 π 之间有无数个值, 我们并不能把无数个值加起来,再除以无穷大.
实际上在数学中常常会有这种感觉, 你隐约觉得应该把连续区间上无数多个值加起来, 虽然你并不能真的这么做. 通常当你产生这种直觉时, 积分便是解决问题的核心.
![]()
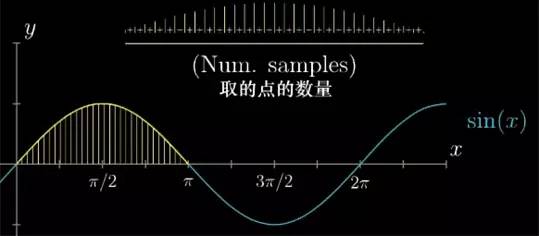
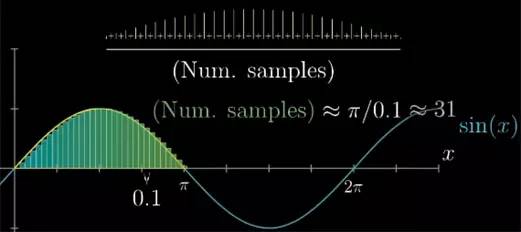
通过计算有限数值的和来估算答案是一个不错的开始, 在正弦函数中, 假设区有限个点均匀分配在区间上. 因为点的数量是有限的,所以你可以把它们的高度 sin(x) 加起来, 然后再除以点的数量得到平均值.
假如无数个点的平均值是有意义的话, 那我们取越多的点来计算高度的和, 计算出的平均值就应该越接近连续变量实际的平均值.
![]()
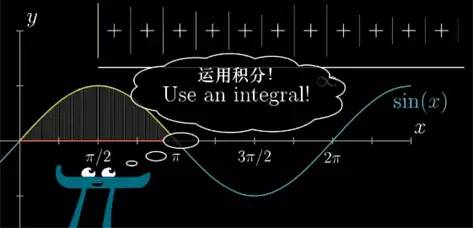
你应该至少觉得这与 sin(x) 在 0 到 π 之间的积分有点联系. 虽然一开始你可能不清楚具体的联系是什么.
回忆一下对于 sin(x) 函数的积分,你也会考虑在函数上取一些点. 但我们不是各个点的高度加起来,然后除以点的个数.
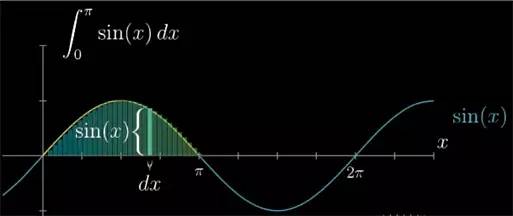
而是将 sin(x)*dx 加总起来(dx 是点间的距离). 也就是说加起来很多个小矩形的面积,而不是指的高度. 准确而言,积分并不完全是这些面积的总和. 而是当 dx 逼近 0 时候, 小矩形面积总和的极限.
![]()
但借助计算有限个长方形的面积总和的方法, 我们可以更好的理解积分. 现在我们可以重新把平均值的这个表达式, 即这点高度的总和除以点的数量用点间的距离 dx 来表达出来.
如果点间的距离是 0.1,而且你知道定义域是从 0 到 π. 你能计算出一共有多少个点吗?你可以用这段区间的长度 π 除以间距的长度. 如果结果不是整数,你可以取整. 这样带来的误差是可以接受的.
![]()
所以如果我们将两点间的距离记为 dx, 点数量就是 πdx
π
dx
. 将表达式中的分母替换为 πdx
π
dx
, 并将 dx 挪到分子中.
想一想把 dx 挪到分子上面的意义, 这就意味着把形如 sin(x)*dx 的项加了起来,对应着不同 x 的值. 于是,分子看上去就是积分的表达式.
![]()
随着取得点数量的增加, 求出的平均值就越来越接近 sin(x) 从 0 到 π 的积分, 除以区间的长度 π.
换句话说图像的平均高度就是区域的面积除以宽度.
现在让我们实际计算一下这个表达式. 上个视频中我们讲到想要计算积分, 就需要求函数的原函数. 那么什么函数的导数是 sin(x) .
如果你对三角函数足够熟悉的话,你就会想到 cos(x) 的导数是 -sin(x). 再加上一个符号, 那么 -cos(x) 就是 sin(x) 的原函数.
![]()
为了防止出错,我们来看一眼 -cos(x) 的图像, 在 x=0 处斜率是 0 , 接着斜率不断变大, 在 π2
π
2
处取到最大值. 然后在 π 处斜率又变回 0 .
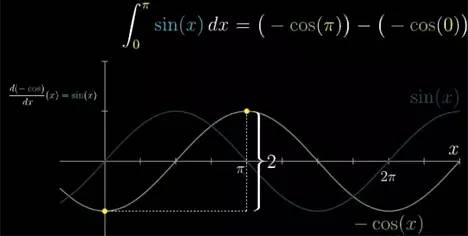
整体来看 -cos(x) 的斜率处处都和 sin(x) 相等. 那怎么计算 sin(x) 从 0 到 π 之间的积分呢? 我们要用原函数在上界的值减去在下界的值. 更直观的来看,这就是 -cos(x) 得图像在 π 处和 0 处的高度差. 如下图所示, 高度差恰好是 2.
![]()
我们所求的正弦函数下方的面积刚好就是 2. 所以我们所求的平均高度, 即定积分的值除以区间的宽度, 就是 2π
2
π
, 大约就是 0.64.
![]()
问题的,最开始我曾说过函数的平均值,提供了另一种角度. 去看待为何积分和求导是互逆的运算. 为何一个函数图像下的面积与另一个函数的斜率有关.
请注意求平均值 2π
2
π
归根到底就是原函数 -cos(x) 在区间上取值的变化除以区间的长度.
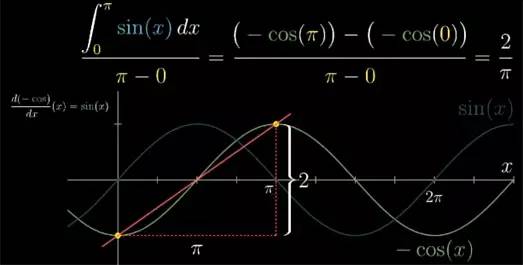
另一种思考方式是将这个分式看作原函数 x=0 处和 x=π 处两点连线的斜率.
![]()
现在你可以开始思考, 为什么这个斜率代表 sin(x) 在 0 到 π 之间的平均值了?根据定义 sin(x) 是原函数 -cos(x) 的导数. 它给出了 -cos(x) 在每个点上的斜率. 所以 sin(x) 的平均值就是原函数从 x=0 到 x=π 所有切线斜率的平均值.
从这个角度考虑, 在某一区间上所有切线的平均斜率, 不就应该等于起点和终点连线的斜率吗?
![]()
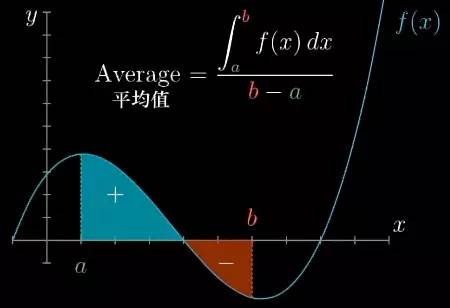
为了更好的消化这一概念,让我们看看任意的一个函数. 对于任意函数 f(x), 如果想求出它在某一区间的平均值,比如从 a 到 b. 你就要求出 f 在区间上的定积分,然后除以区间的宽度 b - a. 你可以把这个想象成图像下区域的面积除以宽度. 更准确的说,这个面积是有正负之分的,在 x 轴下面的面积计算负数.
现在请思考一下这个面积与有限个数值的平均值, 也就是有限个数的和除以它们的个数有什么联系?
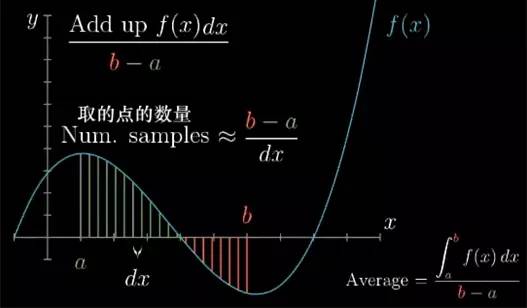
当我们取一系列间距是 dx 的点时, 点的数量是区间长度除以 dx. 所以如果把这些点的 f(x) 加起来,然后除以点的数量, 结果就等于把 f(x)*dx 加起来再除以整个区间的长度.
![]()
两者之间唯一的区别在于积分考虑的是 dx 趋近于 0 的情况, 但这恰好对应了取越来越多的点, 近似出来越来越准确的平均值.
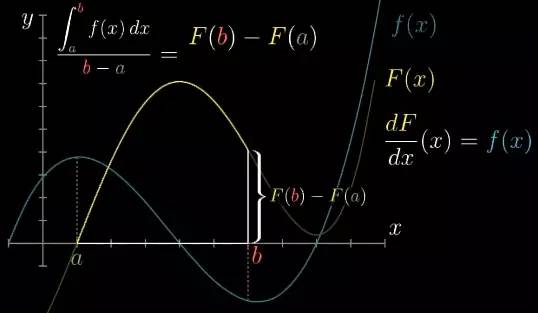
计算任意函数的积分归根结底就是寻找它的原函数, 一般用大写的 F(x) 表示. 具体而言,我们求的是原函数从 a 到 b 上的变化 F(b)-F(a). 你可以把它想成原函数从起点到终点的高度差
![]()
方便起见,我们选择这个原函数,下界的值为 0. 但请记住你可以任意的将一个函数上下平移,加减任意的常数. 平移后得到的新函数依旧是正确的原函数.
所以函数平均值问题的解决方法就是用新的函数从 a 到 b 的高度变化,除以 a 到 b 的长度. 换句话说,也就是原函数在这个区间的起点和终点连线的斜率.
所以为什么原函数就是解决积分问题的关键呢?一种直观的想法,在上一个视频中已经讲过了,现在从另一种角度来考虑, 当你求解连续函数的平均值, 转化为求解另一个函数各点切线的平均斜率时. 你可以仅仅只考虑起点和终点, 而不用去考虑任何的中间点.
在上一个视频中我们讲述了在什么情况下应该想到用积分. 也就是说当你手头上的问题可以通过细分然后再相加的方式估算的话,那么就试一试用积分来解决.
这里还有第二种情况,应该要想到利用积分作为解决问题的工具. 如果在有限个数量的情况,你懂得怎么用相加的方式解决问题. 例如求一些数的平均值, 然后需要推广到连续的变量,也就是无穷无限个数量的话, 你可以试试用积分来描述这个问题. 这种解决问题的方式时常出现在概率问题中.
「予人玫瑰, 手留余香」
如果感到本文有些许帮助, 感谢转发, 支持本号更快发展!
拨开知识的层层密林,探寻美妙数学中的趣味。
感谢关注遇见数学!