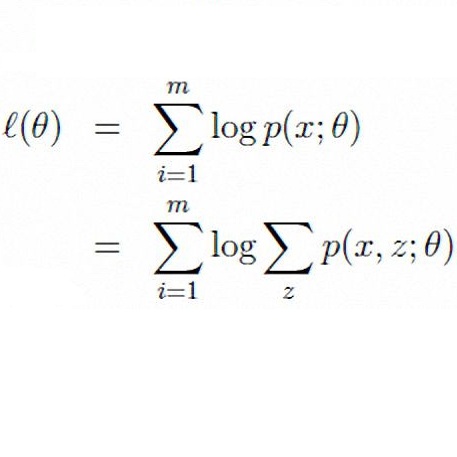干货|通俗易懂地解释EM算法并举例说明?

推荐阅读时间：5-10min

主要内容：极大似然估计和EM算法

以下是我觉得最通俗理解EM思想的方式了！之前做的笔记，详细看来：

1

极大似然估计

讲EM算法之前，我们先来看下极大似然估计，这个在掌握机器学习数学基础之概率统计（重点知识）这篇文章有讲解，而EM算法是为了解决“最大似然估计”中更复杂的情形而存在的。 

这里“极大似然估计中更复杂的情形”是什么情形呢？ 我们知道极大似然估计是求解实现结果的最佳参数θ，但极大似然估计需要面临的概率分布只有一个或者知道结果是通过哪个概率分布实现的，只不过你不知道这个概率分布的参数。而如果概率分布有多个呢或者你不知道结果是通过哪个概率分布实现的？

于是别说去确定“这些概率分布”的最佳参数了，我们连最终结果是根据哪个概率分布得出来的都不知道，这就是EM算法要面临的情况了。

2

EM算法

最大似然估计和EM算法都是根据实现结果求解概率分布的最佳参数θ，但最大似然估计中知道每个结果对应哪个概率分布（我知道哪个概率分布实现了这个结果），而EM算法面临的问题是：我不知道哪个概率分布实现了该结果。怎么在不知道其概率分布的情况下还能求解其问题？且看EM算法：

EM算法的求解思想

在说明EM算法的求解思想前，我们先总结下上面的内容。

一般的用Y表示观测到的随机变量的数据，Z表示隐随机变量的数据(因为我们观测不到结果是从哪个概率分布中得出的，所以将这个叫做隐变量)。于是Y和Z连在一起被称为完全数据，仅Y一个被称为不完全数据。

这时有没有发现EM算法面临的问题主要就是：有个隐变量数据Z。而如果Z已知的话，那问题就可用极大似然估计求解了。 于是乎，怎么把Z变成已知的？

举个日常生活的例子。

结果：大厨把锅里的菜平均分配到两个碟子里

难题：如果只有一个碟子乘菜那就什么都不用说了，但问题是有2个碟子，而因为根本无法估计一个碟子里应该乘多少菜，所以无法一次性把菜完全平均分配。

解法：大厨先把锅里的菜一股脑倒进两个碟子里，然后看看哪个碟子里的菜多，就把这个碟子中的菜往另一个碟子中匀匀，之后重复多次匀匀的过程，直到两个碟子中菜的量大致一样。 上面的例子中，平均分配这个结果是“观测数据”，为实现平均分配而给每个盘子分配多少菜是“待求参数θ”，分配菜的手感就是“概率分布”。于是若只有一个盘子，那概率分布就确定了（“把锅里的菜全部倒到一个盘子”这样的手感是个人都有吧），而因为有两个盘子，所以“给一个盘子到多少菜才好”的手感就有些模糊不定，不过我们可以采用上面的解法来实现最终目标。

理解EM算法最好的方式我觉得就是结合这些类比去理解，然后那些数学公式是怎么来的，这样就可以事半功倍了！请看下面：

EM算法的思想就是：

1. 给θ自主规定个初值（既然我不知道想实现“两个碟子平均分配锅里的菜”的话每个碟子需要有多少菜，那我就先估计个值）；

2. 根据给定观测数据和当前的参数θ，求未观测数据z的条件概率分布的期望（在上一步中，已经根据手感将菜倒进了两个碟子，然后这一步根据“两个碟子里都有菜”和“当前两个碟子都有多少菜”来判断自己倒菜的手感）；

3. 上一步中z已经求出来了，于是根据极大似然估计求最优的θ’（手感已经有了，那就根据手感判断下盘子里应该有多少菜，然后把菜匀匀）；

4. 因为第二步和第三步的结果可能不是最优的，所以重复第二步和第三步，直到收敛（重复多次匀匀的过程，直到两个碟子中菜的量大致一样）。

而上面的第二步被称作E步（求期望），第三步被称作M步（求极大化），于是EM算法就在不停的EM、EM、EM….，所以被叫做EM算法！

注意：数学详细推导这里不会给出，其他答案和网上有详细推导。记得类比知识，还有学下前置知识（比如Jensen不等式）就好！

转自：机器学习算法与自然语言处理

完整内容请点击“阅读原文”