相关性的测量与解释 |《别拿相关当因果》

培养严谨的思维方式
在不借助任何专业知识的前提下，准确定位问题

下文节选自《别拿相关当因果！因果关系简易入门》, 已获出版社授权许可, [遇见数学] 特此表示感谢! 

相关性的测量与解释

比如我们调查了一些学生在期末考试前喝了多少杯咖啡，然后又记录了他们的期末考试成绩。这个案例的假设数据如图 3-3a 所示，两个变量之间的相关性非常高，相关系数接近 1（确切地说是 0.963），所以图上的黑点似乎紧紧地聚在一条无形的直线两侧。如果我们将这一关系反过来（于是不喝咖啡的学生考试成绩成了 92 分，而喝 10 杯咖啡的学生考试成绩则为 10 分），建立一种负向联系，那么相关变量的变化幅度是一样的，唯一改变的就是相关系数的符号。在这种情况下，这个相关系数会接近-1（-0.963），刚好是正相关数据图水平翻转过来的样子（如图 3-3b 所示）。

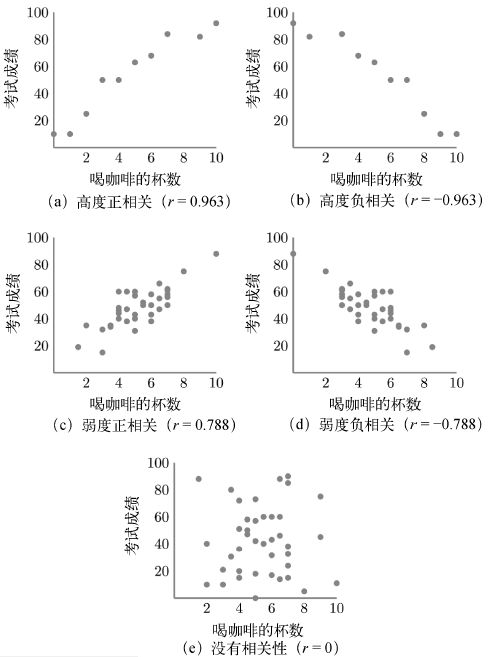
图3-3 喝咖啡的杯数和考试成绩之间不同强度的相关性

如果将每两个变量之间的关系都变得更弱一些（每次喝同样杯数的咖啡，但考试成绩的变化更大），那么这些黑点就会更为分散，变量之间的相关性也会更低。如图 3-3c 所示，图中的黑点绝大部分仍然呈直线排列，但是偏离中心的距离却要远得多。我们再一次将两个变量之间的关系调转过来（让喝咖啡与更差的考试成绩相关），然后就得到了图 3-3d，两张图唯一的区别在于一个是上坡面，另一个是下坡面。

向上滑动阅览简介及目录 

作者者：Samantha Kleinberg
译者者：郑亚亚
出版社：人邮出版社图灵新知

长按上面二维码或
点击 【阅读原文】
跳转遇见微店购买

本书是写给普通人的因果逻辑入门书，旨在帮助读者培养严谨的思维方式，在不借助任何专业知识的前提下，准确定位问题。主要内容包括：认识原因，对原因的理解和运用，如何只通过观察找到原因，大数据集与原因的关系，因果关系相关实验，如何利用因果关系来制定有效的干预措施，研究因果关系的意义。
本书适合所有对探究事件真相感兴趣的读者，无须统计学等专业背景。

本书赞誉    阅读    

前言    阅读    

第 1 章　引子    阅读    

第 2 章　心理    

第 3 章　相关性    

第 4 章　时间    

第 5 章　观察法    

第 6 章　计算法    

第 7 章　实验法    

第 8 章　解释    

第 9 章　行动    

第 10 章　展望    

致谢    

参考文献    

注意，当一个变量与另一个变量之间的关系变弱时，要根据喝咖啡的数值来找到考试成绩就难多了，反之亦然。这一点从图上也可以明显地看出来，在前两个例子中，选择一个变量的数值极大地限制了另一个变量可能的数值。然而，如果我们在相关性较弱的情况下，试图预测一个人喝了四杯咖啡后可能会考出的成绩，那么我们的预测将远远不及前面的例子那么准确，因为这时喝四杯咖啡的人考试成绩变化的范围比之前要大得多。变量之间这种不断增加的变化的极限就是变成两个完全不相关的变量（相关系数为零，如图 3-3e 所示），在这种情况下，我们将无法根据饮用的咖啡数量来对考试成绩做出任何预测。

如果我们想知道人们居住的位置和是否开车之间有多强的相关性， 应该怎么做？到目前为止，我们介绍的测量相关性的方法一般都用于测量连续值数据（比如股票价格），而不用于测量离散值（比如位置类型或电影类型）。如果我们只有两个变量，而且每个变量只有两个值，那我们就可以用皮尔逊相关系数的简化版——Phi 相关系数。

比如说，我们可以测试人们的居住位置和是否开车之间的相关系数。位置信息要么是市区，要么是郊区或乡下，而开车情况则要么是开车，要么是不开车。和之前一样，我们要测试这些因素是如何共同发生改变的， 但此处的“改变”指的是我们看到这两个变量共同出现的频率（而不是这两个数值如何增减）。表 3-1 展示的是数据可能会呈现出的样子。在这个表格中，数据的 Phi 相关系数是 0.81。而我们主要观察的是，测量出来的绝大部分数据是否落在了表格的对角线上。所以，如果绝大部分数值都聚集在“开车/非市区”和“不开车/市区”周围，那么这两个变量之间就存在正相关性。如果绝大部分数值都聚集在另一条对角线上，那么相关性不变，但是相关系数前的符号相反。

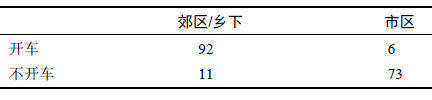
表3-1 居住位置和开车情况的各种组合

然而，相关性强并不一定意味着相关系数也高。皮尔逊相关系数假定两个变量之间是线性关系，即一个变量（比如身高）增大，另一个变量（比如年龄）也会以相同的比率增大。然而，情况并非总是如此，因为还可能存在更为复杂的、非线性的关系。如果不喝咖啡会让人精神不振（并且会降低考试成绩），但是咖啡喝得太多又会让人神经过敏（并且影响考试发挥），那么把我们收集到的一些数据画出来可能就是图 3-4 中的那条曲线。在这个图中，人们喝咖啡的杯数从 0 增加到 5 时，考试成绩是持续上升的，然后在 5 到 10 杯之间，考试成绩随着喝咖啡杯数的增加而慢慢下降。尽管这个案例中的皮尔逊相关系数刚好为零，但是这些数据却呈现出了明显的规律性。很多因果推理方法都很难推理出这种关系，我们将在 后面的章节中继续讨论这个问题。鉴于生物医学（比如缺乏维生素或维生素服用剂量过多都可能导致健康问题）和金融（比如将税率和收入联系在一起的拉弗曲线）等应用领域都存在这一问题，所以很值得我们去认真思考一下。

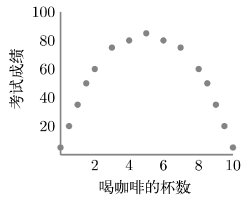
图 3-4  非线性关系（r = 0.000）

类似地，如果孩子们的体重总是随着年龄的增长而增长，但是体重是以指数级增长的（随着年龄的增长，体重增长得越来越多），那么皮尔逊相关系数会比想象的要低，因为这个指标适用的是线性关系。这就好比我们将数据输入黑匣子，然后不管黑匣子反馈给我们的是什么数字都不假思索地接受，这样是很危险的。在这些相关性被低估甚至看起来是零的案例中，如果我们不进一步研究就直接接受这样的数值，很有可能会错失一些十分有意义的关联。

这就是我们不能把相关系数（不管是皮尔逊相关系数还是其他相关系数）为零理解为不存在任何相关性的部分原因（还有很多其他原因，比如测算中的失误或者导致结果出现偏差的异常值）。另外一个主要原因是， 我们所用的数据可能不具代表性，不能反映数据的基本分布情况。如果只使用医院的入院数据和急诊科数据来研究流感致死情况，那我们得到的流感死亡率就会比社会整体人群的实际流感死亡率高得多。这是因为病人一般是因为症状比别人更严重或者还有其他疾病才会去医院（而且去医院的流感病人可能更容易死于流感）。所以我们看到的并不是流感导致的所有结果，而是流感病毒在那些有其他疾病或者流感症状十分严重的病人身上导致的结果。

为了解释限定范围问题，我们假设有两个变量：SAT 总成绩和学习时间。然而，我们并没有所有 SAT 考生的成绩数据，只有那些数学和语文成绩总分超过 1400 分（图 3-5 中的灰色区域）的考生的成绩数据。在这个假设的数据中，成绩好的考生包括那些天生擅长考试的考生（他们不学习也能考得好）和后天刻苦学习的考生。如果仅使用灰色区域的考生的成绩数据，我们是无法找到这两个变量（SAT 总成绩和学习时间）之间的相关性的。但如果我们使用的是所有考生的考试成绩数据，就会发现这两个变量之间存在很强的相关性（灰色区域的考生的学习时间与考试成绩之间的皮尔逊相关系数为零，而在整个数据集中，二者的皮尔逊相关系数为0.85）。所以说，我们可以通过以某种结果为限定条件（只研究出现某种结果的案例），然后从毫无关联的变量之间找到相关性。如果 SAT 成绩好且课外活动丰富的学生能够被名校录取，那么仅来自于这些高校的数据则会显示 SAT 成绩和很多课外活动之间存在某种相关性，因为在这个群体中，这两个变量（SAT 成绩好且参加很多课外活动）往往是同时出现的。

图 3-5 灰色区域的数据代表的是一个限定的范围

这种抽样偏差十分常见，想想那些调查访客政治观点的网站。网站的访客并不是从人群中随机抽取的调查对象。那些带有极端政治偏见的网站的访客，其政治观点与一般人的政治观点之间的偏差就更大了。如果某个网站的所有访客都是现任总统的坚定支持者，那么该网站的调查结果可能会显示，该总统每发表一次重要演说，他的支持率都会上升。但是，这个结论所反映的支持率和重要演说之间的相关性只存在于那些本就喜欢这个总统的人身上（因为接受这个调查的正是这群人）。我们将在第 7 章讨论不同类型的抽样偏差（比如存活者偏差），因为这些偏差会影响我们从实验数据中得出的结论。

有一点需要牢记：我们之所以会找到一些错误的相关性，除了数学方面的原因之外，另一个原因是人们在观察数据时可能会发现一些虚假的规律。有些认知偏差会让我们在无关的因素之间推断出联系，这和抽样偏差相似。比如证实性偏差会使人们去寻找证据来证实他们的观点。如果你认为一种药物会引起某种副作用，那你有可能会去网上搜索其他吃了这个药并且出现了这种副作用的病人。但是，这种做法意味着你是在忽略所有不能证实你的假设的数据，而不是寻找那些有可能让你重新评估你的观点的证据。证实性偏差可能还会导致你对那些与你的假设相矛盾的证据产生怀疑——你可能会认为这些证据的来源不可靠，或者获取这些证据的实验方法有问题。

人们除了在寻找和使用证据时存在偏差，在解释证据时也可能存在偏差。如果一种新药正在接受临床测试，而一名医生已经知道有病人正在服用这种药，并且认为这个药对病人是有帮助的，那么在这种情况下，他就有可能会去寻找迹象来证明这个药物是有效的。由于病人的很多指标都是主观的（比如运动强度和疲劳程度），这就有可能导致医生对这些指标的估算存在偏差，并导致医生推理出一个并不存在的相关性。这个例子来自于一项真实的研究，在这项研究中，发现药物有效的都是那些知情的医生（我们将在第 7 章详细介绍这项研究，并且介绍盲测的重要性）。因此，先验观点不同的人可能会对数据做出不同的解释，从而得出不同的结论。

“错觉相关”是证实性偏差的一种特殊形式，它指的是看到一个实际上并不存在的相关性。关节炎症状和天气之间可能存在着一定的联系，这种联系广为流传以至于人们常常把它当成事实。但是，病人知道这一联系后就有可能会说这两者之间存在相关性，但这不过是因为病人对这种相关性已经有了心理上的预期。然而，当研究人员综合考量了病人自述、临床医生的评价和一些客观的测量数据，试图客观地研究这一相关性时，却发现这两者之间并没有任何相关性（其他研究人员已经发现，真正的罪魁祸首可能是空气湿度，但是这一结论并不令人信服）。事实上，当我们把那些关于病人自述的关节疼痛和气压之间关系的数据展示给一些大学生时，他们不仅在没有相关性的时候说看到了相关性，而且在完全一样的序列中找到了正相关性和负相关性。

这种偏差和抽样偏差很相似。我们之所以会错误地认定某种相关性，是因为我们只关注了一部分数据。如果你期望变量之间存在负相关性，那么你就有可能只关注整个数据集中那些能够证实这一观点的一小部分数据。这就是它是一种证实性偏差的原因：人们有可能因为先验的信念而自动将目光投向某些数据。在关节炎与天气的案例中，也许人们对某些证据太过重视（忽视了天气好时关节疼痛的例子，重点突出天气不好时关节疼痛的例子），也许人们看到了一些实际上并不存在的证据（根据他们所预期的联系和天气的变化来讲述不同的症状）。

☟ 点击【阅读原文】进一步查看或购买此书