【泡泡航行天下】用于微型无人机规划的稀疏三维拓扑图（IROS）

会员服务 ·

【泡泡航行天下】用于微型无人机规划的稀疏三维拓扑图（IROS）

2019 年 9 月 18 日 泡泡机器人SLAM

泡泡航行天下，带你精读机器人顶级规划会议文章

标题：Sparse 3D Topological Graphs for Micro-Aerial Vehicle Planning

作者：Helen Oleynikova, Zachary Taylor, Roland Siegwart, and Juan Nieto，Autonomous Systems Lab, ETH Zurich

来源：IROS 2018

编译：郑宇

审核：杨小育

欢迎个人转发朋友圈；其他机构或自媒体如需转载，后台留言申请授权

摘要

大家好，今天为大家带来的文章是——一种用于微型无人机规划的稀疏三维拓扑图，该文章发表于IROS 2018。

微型无人机（MAV）具有在三维空间中自由运动的优点。但是，创建可有效用于规划此类机器人的紧凑和稀疏地图表示仍然是一个有待解决的问题。本文以噪声传感器数据为基础，构建一个用于三维规划的包含拓扑信息的稀疏地图。我们使用欧几里德符号距离场，提取三维广义Voronoi图（GVD），并获得表示环境拓扑结构的骨架（skeleton）图。然后我们将这个骨架图转换为稀疏图，我们显示它对噪声和分辨率的变化是有抵抗力的。我们展示了该稀疏图的全局规划，并提供了超过其他常见规划方法的数量级加速。我们使用RGB-D传感器在MAV上构建的真实地图中验证我们的规划算法。

主要贡献

1、提出了一种从密集体素网格中的真实噪声传感器数据中提取骨架图的新方法。。

2、提出了一种构造稀疏直线连通图的方法，用于快速规划，可抵抗噪声和分辨率的变化。。

3、规划评估显示我们的方法比其他全局规划方法快几个数量级。

算法流程

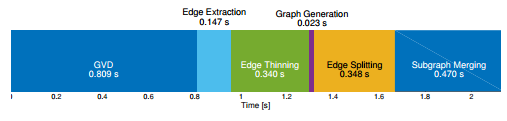
图 1 生成骨架图（这是一个密集的体素网格）的步骤的系统图，并从那里得到的稀疏图（这是一个带有直线边的无向图）。步骤的一般顺序是生成空间的广义Voronoi图（GVD）或中轴，提取其边和顶点，细化图，然后沿着图中的边创建稀疏图，并重新连接最终图中的断开连接的子图。

骨架图构建

SKELETON DIAGRAM CONSTRUCTION

我们的方法包括两个主要部分：第一，在体素空间中构建一个体素厚的骨架图，保留原始空间的拓扑和连通性，同时尽可能少的元素，如图2中的二维所示。这是与Lau等人使用的2D拓扑图最接近的类比。其次，从图中生成稀疏图，其不再绑定到体素空间，而是由通过直线边连接的图顶点组成。

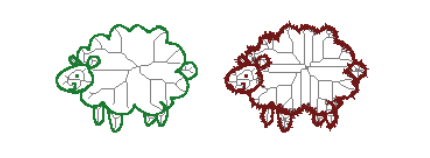
图 2 噪声对Voronoi图的影响。左边的图像没有受到噪声干扰，有一个非常稀疏图表。通过噪声传感器测量生成的右边图像在图中具有更多边缘。这项工作的一部分重点是在地图中存在重度传感器噪声的情况下修剪Voronoi图。

1、GVD（广义Voronoi图）生成

为了生成原始的广义Voronoi图，我们采用了在有符号距离函数中找到“脊”的常见方法。寻找GVD类似于找到自由空间中轴的离散化，这在二维机器人规划问题中已被充分研究。在二维中，中轴由连接线组成，最大化与障碍物的距离，如图2所示。但是，由于中轴的尺寸比原始形状小一个尺寸，因此将其推广到三维时，中轴由（可能是弯曲的）平面组成，以最大化距离。为了使问题尽可能稀疏以进行规划，我们放弃平面表示，而是寻找中间曲线骨架，其由三维中的1体素粗线组成。这类似于三维GVD的边缘和顶点，放弃了面。

我们从与Foskey等人相同的一般方法开始，找到属于中轴的所有点。为此，我们迭代ESDF中位于自由空间中的所有体素，并将其父方向与其6个连接邻居的父方向进行比较。每个体素将方向存储到物体表面上的“父”点（与体素最近的占据点）。请注意，我们也可以遵循Lau et的2D方法并存储来自波前终止的GVD候选者，以避免必须检查地图中的所有体素。

当中轴由CAD生成的数据构成时，如果知道哪个表面属于哪个目标，则可以检查相邻的目标是否具有不同的父目标或基目标。然而，如图2所示，对于嘈杂的现实世界数据和离散化的地图表示，很难分辨哪些点属于哪些目标，并且表面边界上的噪声产生许多虚假的中间线。

为了解决这个问题，我们调整了θ-SMA方法，该方法基于基点之间的最小θ角创建简化的中轴线（SMA）。在我们的离散化ESDF中，我们使用以下方法计算点是否属于中轴：

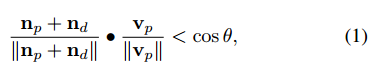
其中vp是当前体素的父方向，nd是从相邻体素到当前体素的方向，并且np是相邻体素的父方向。
通过此检查意味着该点在目标边界上具有至少两个不同的基点。

2、边缘提取

既然我们拥有属于中轴的所有点，我们需要将它们分类为边，顶点和面，因为我们的目标是只保留稀疏描述空间拓扑的单体素细线。

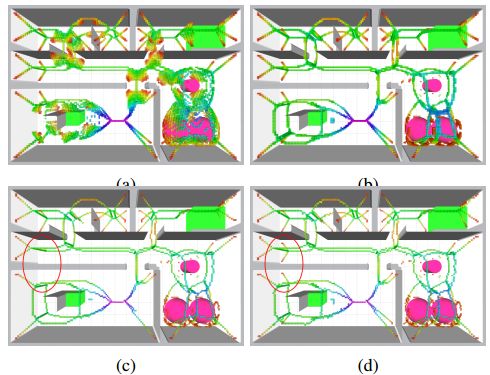
图 3 生成中轴/ GVD边缘的不同方法。（a）显示通过计算基点数生成的边缘，（b）显示由同样位于中轴线上的相邻点数量生成的边，（c）显示使用拓扑保持腐蚀技术稀释的（b）边缘，最后（d）显示应用相同的技术，但没有扩展的终点检查，特别注意保留在红色圆圈中的边缘。颜色表示到障碍物的距离。

在完美建模的环境中，三维GVD的边缘被定义为具有三个基点，而顶点定义为具有四个基点。然而，由于离散化误差以及实际Voronoi的边界落在体素之间，一些边缘消失并且通过该定义出现假边缘，如图3（a）所示。

由于Voronoi边界也是中间表面的边缘，因此我们选择一种对离散误差和边界噪声更稳定的方法：提取中轴的边缘，以创建中间线。我们使用体素的26个连接邻居属于中轴的度量来确定它是否是边缘。我们保留了至少18个邻居的所有体素，在图3（b）中创建了厚而完整的骨架。

3、稀释

为了消除假双线，我们参考数字拓扑文献，该文献使用递归细化从离散化的形状构建三维骨架。

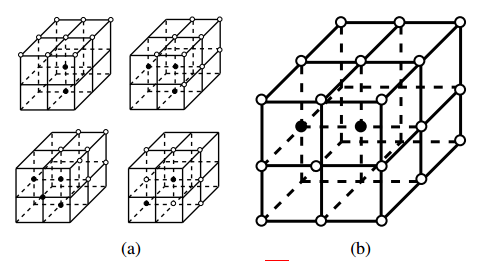
图 4 用于细化的体素模板，（a）是其中的4个删除模板，（b）是我们用于检查点是否是6-连接角的模板。黑点表示前景点（在我们的例子中是GVD边缘点），白色是背景（非边缘点），未标记的匹配前景点和背景点。

我们采用Lee等人描述的一般方法，该方法还允许并行的细化操作。首先，根据几个删除模板之一检查形状中的所有体素。我们选择使用She等人的模式，因为它们简单并且不需要超过每个体素的3×3邻域，如图4（a）所示。根据这些模板评估中心体素的邻域。在模板中，点可以是前景（黑色，边或顶点邻居），背景（白色，面或非GVD邻居），或“不关心”（未标记）。“不关心”点可以匹配任何一个值。

一旦显示一个点与其中一个模板（或其任何90°旋转或镜像操作）匹配，如果它是一个简单的点就可以删除它：即，如果没有它的情况下可以保留其邻居的连通性，且不是终点：有多个26个连接的邻居。此定义既适用于连接的前景体素组（使用26连接连接）和连接的背景体素（使用6个连接进行连接）。因此，为了验证一个点是否简单，我们需要验证其附近的连通组件的数量在没有它的情况下是否保持不变。我们使用Lee等人提出的八叉树邻接测试来做到这一点。

但是，由于我们的边缘提取启发式产生了6个连接的边缘，因此移除所有非端点的简单点会导致错误地移除某些对角线边缘。这是由于端点测试的简单性：6连接端点实际上有2 个26连接的边缘。对任何只有一个6连接邻居的点进行分类会导致许多其他点的保存不正确。（这不是通过细化在中间骨架构造中遇到的问题，因为细化是递归应用的，并且始终只导致26个连接的组件。）

为了解决这个问题，我们使用一个“角模板”扩展端点测试，如图4（b）所示。如果一个点只有一个26连接的邻居，或者如果它只有一个6连接的邻居并且匹配图4（b）中的模板（及其旋转和镜像），则该点被认为是一个端点。

稀疏图生成

SPARSE GRAPH GENERATION

为了进一步细化问题，我们用本节中描述的步骤，使用稀疏图来近似骨架图。

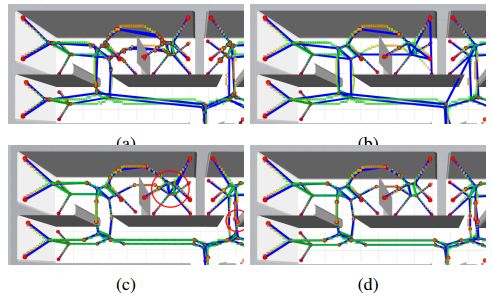
图 5 顶点生成过程中的步骤，红色圆作为稀疏图的顶点，蓝色连接线为稀疏图的边，覆盖在GVD边缘的顶部。（a）显示连接的稀疏图，没有任何顶点修剪。（b）显示k-D树修剪的结果; 可以看出，一些边缘穿过障碍物。（c）显示通过插入新顶点在任何时候偏离直线太远时分割边缘的结果，（d）显示分割也试图匹配到附近顶点的结果（删除（c）中所有顶点附件的重复）。

1、顶点提取

当我们的骨架只有一个体素厚度时，我们能够非常简单地提取顶点：找到具有1个或多于3个 26个连接的邻居的所有边缘体素。其结果如图5（a）所示，红色圆圈表示顶点。可以看出，由于这个定义，附近的顶点有许多冗余顶点。虽然它们在技术上是正确的，但它们会使稀疏图形混乱，并且不会添加新的拓扑不同的路径。

为了确保我们在下一阶段构建的图形尽可能稀疏，我们修剪GVD中的顶点。我们构建了最近顶点的k-D树，并且对于GVD中的每个顶点，找到修剪半径 r_prune 内的所有其他顶点。从这些顶点，保留与障碍物距离最大的那个顶点，并移除所有其他顶点。该操作的结果如图5（b）所示。

2、边缘跟踪

下一步是跟踪从上一节获得的稀疏化顶点之间的直线边。目标是创建一个独立于底层地图分辨率的图形，并且由于预先计算了所有连接信息，因此搜索速度明显更快。

我们从上一步的过滤图顶点开始。为每个顶点分配一个顶点ID，该顶点ID也在图中标记，并插入到顶点ID到顶点信息的映射中。对于每个顶点，我们尝试按照图边缘查找与其他顶点的连接。

这可以通过以下方式完成：首先，对于每个顶点，我们检查其26个连通性邻居的边缘。对于每个边缘，我们通过检查其所有邻居并优先选择与边缘的当前方向一致的那些边缘来递归地跟随它：

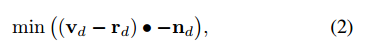
其中vd是到达当前体素的方向，rd是从顶点开始的方向，nd是从当前体素到被检查邻居的方向。

执行该过程直到到达顶点体素，然后找到其在稀疏图中的对应条目，并且创建连接始发体素和新体素的边。

3、边缘分裂

为了防止边缘通过非自由空间，我们对偏离直线路径太远的边缘进行分割。这可以通过以下方式完成：首先，对于图中的每个边，我们使用图A *来找到图中从起始顶点到结束顶点的最短路径。然后将该图边缘中的每个点投影到起始点和结束顶点之间的直线上，并计算其到该线的距离。如果沿该边缘的最大距离超过阈值（例如，我们使用了两倍的体素大小），则在图上具有最大距离的点处创建新的候选顶点。

使每个候选顶点成为一个真实的顶点给出了图5（c）中的结果：当边缘现在与图边缘的形状相匹配，有一些情况下会创建不必要的顶点：即边缘应该连接的附近已经存在顶点的未知。为了抵消这种情况，我们在将候选顶点添加为新顶点之前添加另一个检查：如果候选的r_prune中有另一个顶点，则使用图A *来验证开始和结束顶点是否存在有效连接。仅当连接到顶点候选时，才考虑该顶点候选减少到直线的最大距离。

该最终步骤的结果显示在图5（d）中，其中可以看出，产生了明显更少的额外顶点，并且建立了到现有顶点的更短边缘。

4、修复断开的子图

在某些情况下，对于大而杂乱的地图，例如我们将在下文中使用的迷宫，由于离散化误差，图中存在的一些边缘未在稀疏图中正确地重新连接，这产生了多个断开连接的子图。

我们首先确定子图的数量以及哪些顶点属于它们来解决这个问题。对于图中的每个顶点，如果它没有标记子图ID，我们为其分配一个新的子图ID并执行泛洪填充算法（the flood fill algorithm）来标记属于其子图的所有顶点。泛洪填充算法是一种简单的递归深度优先搜索，其中我们设置每个顶点的标签，跟随该顶点的所有边缘，并继续直到没有边缘可到达的未标记顶点保留。

在标记每个顶点之后，我们执行两个步骤：首先，删除仅包含一个顶点的所有子图。其次，尝试将所有剩余的子图彼此连接起来。

我们通过骨架图使用A *来做到这一点。我们在两个断开连接的子图中选择第一个标记的顶点，并尝试沿着底层骨架图找到它们之间的路径。如果A *能够找到路径，我们将追溯它，检查沿此路径的每个体素。对于分配了稀疏图顶点ID的每个体素，我们记录其ID和标签。当两个连续顶点之间的标签发生变化时，我们在这些顶点之间添加一条边并执行泛洪填充以重新标记新连接的图。

规划算法

PLANNING ALGORITHMS

在本节中，我们将介绍使用ESDF、骨架图和稀疏图中包含的信息进行路径规划的各种方法。对于这些方法中的每一种，我们将MAV建模为具有固定半径的球体。生成的GVD具有该半径的最小距离，因此图中仅存在有效的可穿越节点。

对于前四种规划方法，我们关注的目标是快速找到通过空间的可行初始路径，同时考虑与障碍物的非碰撞作为唯一要求。然后将该初始路径细化为使用多项式样条的MAV的平滑，动力学可行轨迹和微分平坦度的特性，如下面部分所述。

1、使用A* 算法通过ESDF

找到通过空间的路径的最简单方法是在ESDF体素上运行A *。对于每个体素，从起始位置开始，我们扩展其26个连接的邻居，并且如果它们的ESDF距离大于无人机半径，则认为它们是图形的一部分。我们使用到目标的直线距离作为可接受的启发式，并累积体素邻接距离。虽然这种方法是完全分辨率的，但由于图形的大小，它在较大的空间或较小的体素尺寸中变得非常昂贵。

2、使用A* 算法通过骨架图

更快的方法是仅通过骨架图进行搜索。启发式和成本与ESDF A *中的相同，但如果体素是骨架图中的边或顶点，则它被视为有效邻居。一个重要的考虑因素是起点和终点可能不一定在图上。为了解决这个问题，我们从开始向目标开始通过ESDF进行A *搜索，并在扩展同样在图上的顶点时立即中止。我们也向后开始相同的搜索：从目标到开始。这两个搜索快速找到图上的起点和终点。

3、使用A* 算法通过稀疏图

最终的加速是遍历稀疏图而不是底层图，因为无论体素大小或噪声水平如何，图都保持大致相同的大小。我们通过在预先构建的K-D树结构中搜索最近邻居来找到最接近起点和终点的稀疏图顶点。然后我们使用A *来遍历目标顶点的边缘。

4、使用RRT算法通过ESDF

我们还与基于采样的快速探索随机树（RRT）全局规划方法进行了比较。我们评估RRT *，它是概率上最优的（也就是说，它保证在给定无限执行时间的情况下找到最优解）和RRT Connect，它没有最优保证但实际上很快就找到了次优的可行路径。在这两种情况下，我们将未知空间视为已占据，并直接在ESDF中进行碰撞检查。与上面描述的基于搜索的方法不同，后者在解决方案中详尽地搜索地图，基于RRT的方法在规划空间中采样可行点并尝试将它们连接到现有树。一旦目标状态被采样并连接到树，就遍历树以获得最终路径。在RRT Connect中，树从开始和目标两个方向生长。在RRT *中，初始路径继续使用较短路径长度的解决方案进行细化，直到达到时间限制。

5、动力学可行轨迹生成

最后，给定这些方法中的任何一个的初始直线路径，我们需要创建MAV可以满足动力学跟踪的轨迹。我们利用微分平坦的性质来规划动力学可行的多项式样条。由于样条可能偏离初始直线解并且不再是无碰撞，我们使用ESDF距离的局部轨迹优化作为碰撞成本来迭代地“推动”最终轨迹脱离碰撞，如我们之前的工作中所述。

主要结果

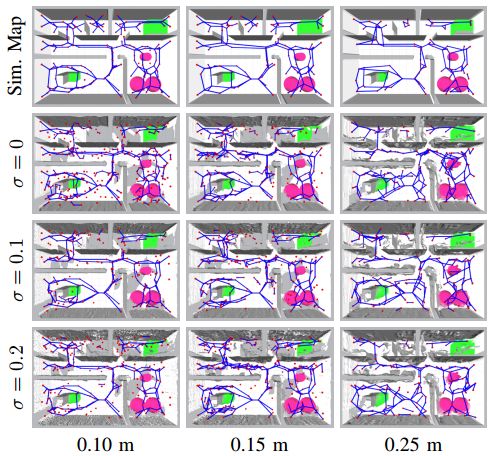
图 6 比较在相同仿真环境中，在不同体素大小和距离测量中的噪声量下生成的稀疏图。第一行是根据地面实际ESDF数据仿真的，而另外三行则显示了使用噪声深度传感器从200个模拟无人机姿势创建的地图。可以看出，尽管由噪声或离散化误差引入了外来边缘，但图的核心结构保持不变。生成的图表最小距离为0.4米。

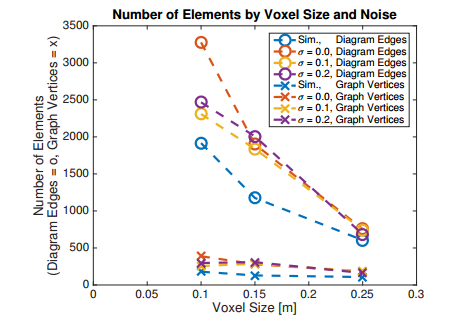
图 7 骨架图（圆圈）和稀疏图（十字）中元素数量的比较。可以看出，体素大小和较小程度的噪声水平对图中元素的数量有很大影响，但图形大小基本保持不变。这意味着图形大小是空间拓扑的函数，而不是地图的分辨率或质量。

图 8 稀疏图（深蓝色边缘和红色顶点）和规划结果通过一个30米 x 30米的迷宫，由MAV在仿真环境中自主探索。绿色显示目标的第一个RRT *路径，黄色是通过ESDF的A *，橙色是通过骨架图的A *，青色是通过稀疏图搜索。

图 9 平台实验的执行时间信息，如背景图所示。地图为20米×22米，体素分辨率为0.07米。在MAV机载计算机上，从ESDF生成稀疏图的总时间为2.13秒。

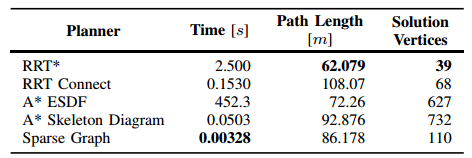
表 1 通过迷宫进行规划的定量结果，如图8所示。我们的方法（稀疏图）比RRT *的初始解决方案快800倍，甚至比RRT Connect快50倍。它产生稍长的路径，因为它绑定到最大间隙图。

Abstract

Micro-Aerial Vehicles (MAVs) have the advantage of moving freely in 3D space. However, creating compact and sparse map representations that can be efficiently used for planning for such robots is still an open problem. In this paper, we take maps built from noisy sensor data and construct a sparse graph containing topological information that can be used for 3D planning. We use a Euclidean Signed Distance Field, extract a 3D Generalized Voronoi Diagram (GVD), and obtain a thin skeleton diagram representing the topological structure of the environment. We then convert this skeleton diagram into a sparse graph, which we show is resistant to noise and changes in resolution. We demonstrate global planning over this graph, and the orders of magnitude speed-up it offers over other common planning methods. We validate our planning algorithm in real maps built onboard an MAV, using RGB-D sensing.

如果你对本文感兴趣，想要下载完整文章进行阅读，可以关注【泡泡机器人SLAM】公众号。

点击阅读原文，即可获取本文下载链接。

欢迎来到泡泡论坛，这里有大牛为你解答关于SLAM的任何疑惑。

有想问的问题，或者想刷帖回答问题，泡泡论坛欢迎你！

泡泡网站：www.paopaorobot.org

泡泡论坛：http://paopaorobot.org/bbs/