1 简介

数值推理任务是指利用数学和逻辑技能解析、理解和解决涉及数字的问题，这在提高数据分析、决策制定和问题解决能力方面至关重要。在过去的工作中，人们通过生成常数表达式或者程序的中间表示来解决数值推理任务。然而，这类中间表示可能并不能很好地和自然语言问题对齐。如图1所示，最上面的例子是常数表达式，同时对齐到一个式子；中间的例子是方程，交错地将自然问题和式子对齐。这种不能很好地对齐，导致模型需要理解完整的问题后，再生成结果，导致生成结果的准确性较低，数值推理性能较差。为了解决这个问题，我们提出用方程作为中间表示。如图1最下面的例子所示，自然语言问题和生成的式子可以很好地对齐，从而降低理解问题的难度，提高数值推理准确性。

2 背景

数值推理是自然语言处理模型处理包含数值信息的文档的必备能力，被广泛应用于金融、科学等领域。通常，数值推理任务是在给定问题的基础上，生成一个数值结果，问题中描述了特定数值，或者不同数值间的关系。由于现有的模型直接处理加法、乘法等数值计算的性能较差，大部分的现有方法先基于问题生成一种中间表示，再根据中间表示计算数值结果。例如，一种常见的中间表示是数学表达式，而目前的SOTA方法是使用程序作为中间表示。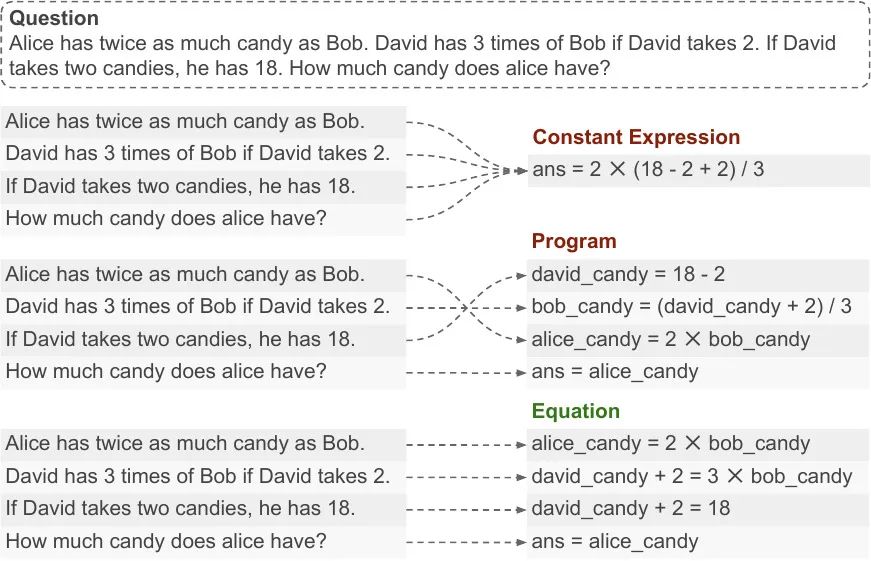图1 不同中间表示的比较

3 动机

从直观角度讲，使用方程作为中间表示要比使用程序的性能更好，因为方程在使用变量前无需对其进行定义，因此比程序语意上更加接近自然语言问题（一个直观的例子如图1所示）。但目前使用大模型生成方程的方法性能并不如使用程序的方法，因为现在大模型的预训练数据中只包含很少的方程。因此在本文中，我们尝试讨论两个问题：

理论上，如何证明使用方程比使用程序作为中间表示要好；
实践上，如何解决现有方法生成方程性能差。

4 方法

4.1 理论角度

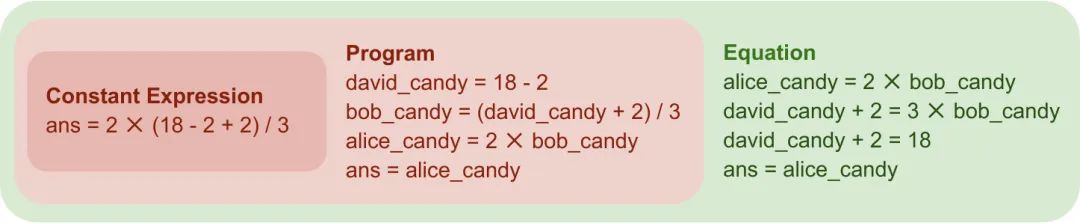
图2 我们理论的直观解释在本工作中，我们给出并证明了一个从理论上比较两种中间表示生成准确性的命题：如果中间表示A是中间表示B的子集，那么生成B作为中间表示的准确性理论上要高于以A为中间表示（如图2所示）。由于程序是方程的一个子集，因此理论上生成方程作为中间表示的准确性要高于生成程序。然而，我们的命题只能从理论上比较两种中间表示的生成准确性。具体实现中，生成准确性还取决于模型的架构、训练数据等多方面因素。因此为了从实践的角度增强大模型生成中间表示的能力，我们需要设计专门的方法。

4.2 方法角度

图3 方法示意图

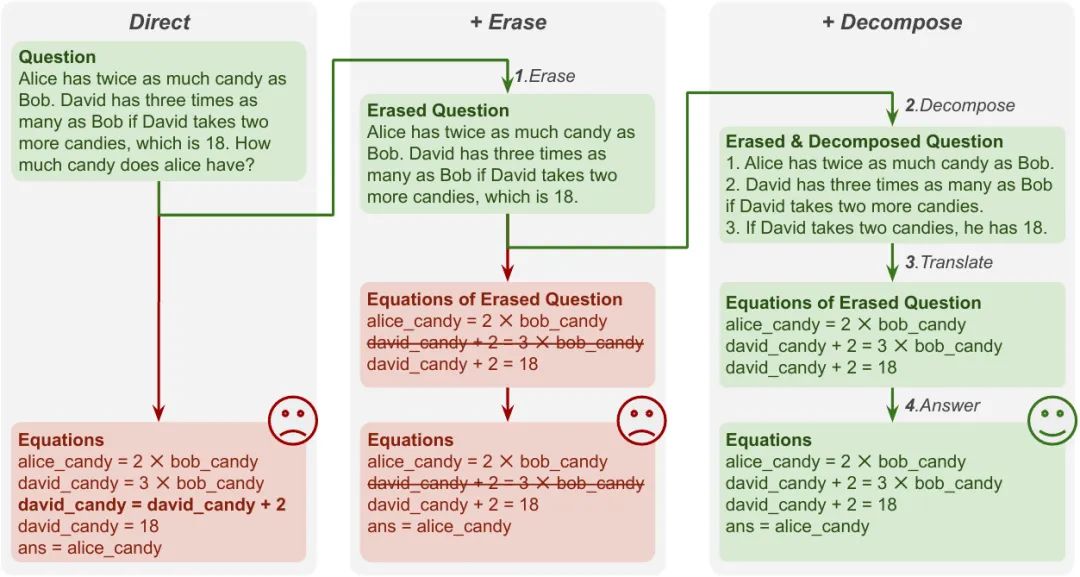
我们基于LLMs生成方程的方法如图3所示。首先，我们会抹除问题中的设问部分，来引导模型生成方程而非表达式或程序。然后，我们会对问题进行分解，来帮助模型更好地将子问题和单个方程进行对齐。

5 实验分析

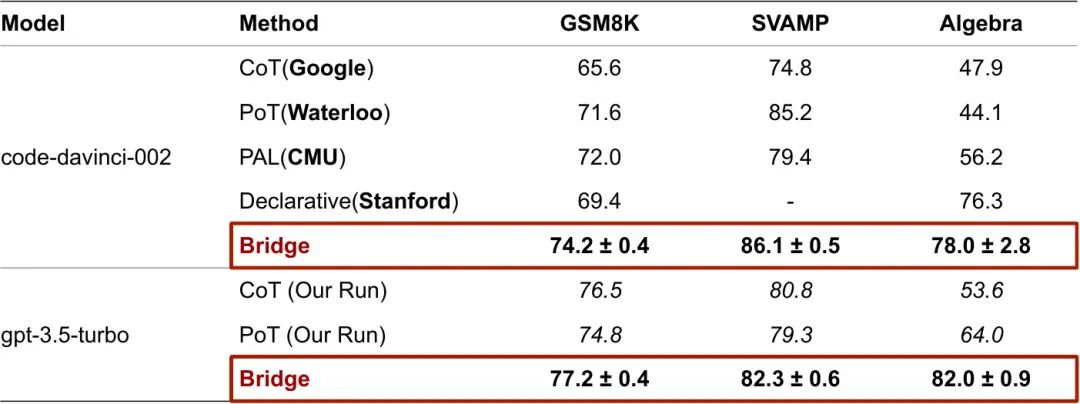
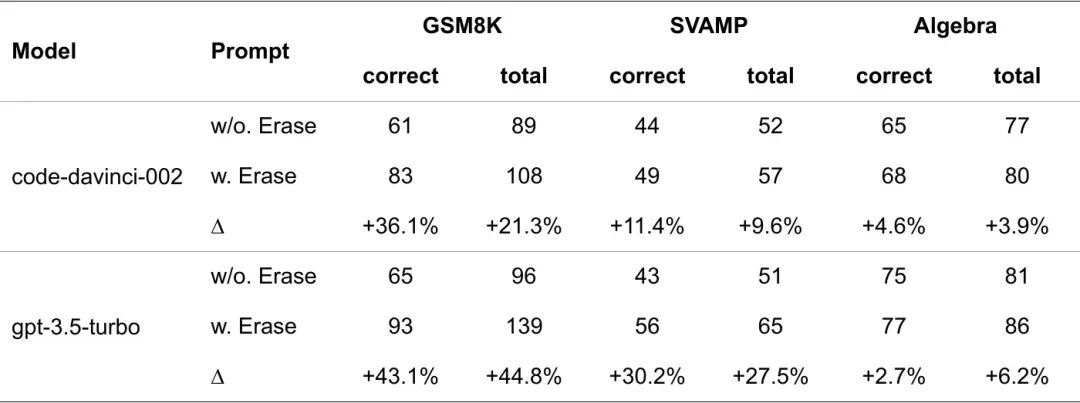
为了验证我们“基于方程的数值推理增强方法”（Boosting numerical ReasonIng by Decomposing the Generation of Equations, Bridge）的有效性，我们在GSM8K和SVAMP上进行了实验，这是两个主流的验证大模型数值推理能力的数据集。表1 主实验我们的方法相对基于程序的方法，在实验数据集上平均提高了2.6%，均取得了SOTA结果（如表1所示），证明了我们方法的有效性。表2 使用我们方法前后的方程比例此外，消融实验表明我们的方法可以提高大模型生成结果中方程的比例（如表2所示），表明我们的方法确实可以提高模型生成数学表达式和程序之外中间表示的倾向。

6 结论

在本文中，我们从理论的角度，给出了方程是比常数表达式或程序更好的数值推理的中间表示，并从实践的角度给出了一套基于大模型生成方程的方法。我们的研究表明：

不同的中间表示会显著地影响数值推理的性能；
通过修改输入的结构，可以帮助模型更好地解决在sft时没有见过的任务

参考文献

[1] McCoy, T.; Pavlick, E.; and Linzen, T. 2019. Right for theWrong Reasons: Diagnosing Syntactic Heuristics in Natural Language Inference. In Proceedings of the 57th Annual Meeting of the Association for Computational Linguistics, 3428–3448. Florence, Italy: Association for Computational Linguistics. [2] Meurer, A.; Smith, C. P.; Paprocki, M.; ˇCert ́ık, O.; Kirpichev, S. B.; Rocklin, M.; Kumar, A.; Ivanov, S.; Moore, J. K.; Singh, S.; Rathnayake, T.; Vig, S.; Granger, B. E.; Muller, R. P.; Bonazzi, F.; Gupta, H.; Vats, S.; boo, A.; Fernando, I.; Kulal, S.; Cimrman, R.; and Scopatz, A. 2017. SymPy: symbolic computing in Python. PeerJ Computer Science, 3: e103. [3] Nie, L.; Cao, S.; Shi, J.; Sun, J.; Tian, Q.; Hou, L.; Li, J.; and Zhai, J. 2022. GraphQ IR: Unifying the Semantic Parsing of Graph Query Languages with One Intermediate Representation. In Proceedings of the 2022 Conference on Empirical Methods in Natural Language Processing, 5848–5865. Abu Dhabi, United Arab Emirates: Association for Computational Linguistics. [5] Patel, A.; Bhattamishra, S.; and Goyal, N. 2021. Are NLP Models really able to Solve Simple Math Word Problems? In Proceedings of the 2021 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, 2080–2094. Online: Association for Computational Linguistics. [6] Paul, D.; Ismayilzada, M.; Peyrard, M.; Borges, B.; Bosselut, A.; West, R.; and Faltings, B. 2023. REFINER: Reasoning Feedback on Intermediate Representations. arXiv:2304.01904. [7] Roy, S.; and Roth, D. 2015. Solving General Arithmetic Word Problems. In Proceedings of the 2015 Conference on Empirical Methods in Natural Language Processing, 1743–1. Lisbon, Portugal: Association for Computational Linguistics. [8] Roy, S.; Upadhyay, S.; and Roth, D. 2016. Equation Parsing : Mapping Sentences to Grounded Equations. In Proceedings of the 2016 Conference on Empirical Methods in Natural Language Processing, 1088–1097. Austin, Texas: Association for Computational Linguistics. [9] Thawani, A.; Pujara, J.; Ilievski, F.; and Szekely, P. 2021. Representing Numbers in NLP: a Survey and a Vision. In Proceedings of the 2021 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, 644–656. Online: Association for Computational Linguistics. [10] Wang, X.; Wei, J.; Schuurmans, D.; Le, Q. V.; Chi, E. H.; Narang, S.; Chowdhery, A.; and Zhou, D. 2023. Self-Consistency Improves Chain of Thought Reasoning in Language Models. In The Eleventh International Conference on Learning Representations.

成为VIP会员查看完整内容