ICML 2022 | 上下文集成的基于transformer的拍卖设计神经网络

关键词**：

**最优拍卖，自动机制设计

导 读

本文是 ICML 2022入选论文《A Context-Integrated Transformer-Based Neural Network for Auction Design》的解读。该论文由北京大学前沿计算研究中心邓小铁课题组与谷歌团队、上海交通大学团队合作完成。本文将基于深度学习的最优拍卖设计的方法论拓展到了上下文拍卖场景中，并为此设计了新的基于 transformer 的神经网络结构。

论文链接：

https://arxiv.org/abs/2201.12489

01

引 言

拍卖设计的一个核心问题是设计满足激励相容并最优化拍卖者期望收益的机制，然而理论的研究陷入了瓶颈。近年来，研究人员开始尝试使用深度学习方法寻找最优拍卖的近似解，这其中的开创工作是 RegretNet [1]。这一套方法论通过将拍卖设计问题抽象化为一个带限制优化问题，用神经网络来构建参数化的机制，并使用标准的机器学习方法来寻找近似最优解。尽管有一系列改进工作，然而目前这套方法论考虑的拍卖场景过于简单：拍卖场景通常限制在固定的买家集合与商品集合上 [1]，或者限制在对称拍卖上[2]。

在这篇工作中，我们将基于深度学习的最优拍卖设计方法拓展到了上下文拍卖中。在上下文拍卖中，买家和商品都具备自己的上下文信息（即辅助信息，或者特征），并且买家对商品的估值分布同时依赖于双方的上下文信息。相比传统贝叶斯拍卖，这是一个更加贴近实际的问题场景。然后，我们为上下文拍卖设计了新的模型 CITransNet，这是一个集成了上下文信息的、基于 transformer 结构 [3] 的神经网络模型。该模型满足排列等价性并且网络规模与输入规模无关。我们通过实验验证了我们这套方法和模型在单物品以及多物品上下文拍卖场景下的有效性。

02

问题描述

我们考虑的上下文拍卖场景是 个买家和 个商品的密封拍卖。与传统贝叶斯密封拍卖不同的是，买家 对商品 的估值服从先验分布 ，其中 和 分别为该买家和该商品的上下文变量。换句话说，买家对商品的估值分布会取决于买家和商品的上下文变量。所有买家和商品的上下文变量集合从联合先验分布采样得到。

拍卖机制包含分配规则与支付规则，分别对应如何将商品分配给买家，以及每个买家支付多少价格。在上下文拍卖场景中，拍卖机制的输入是所有买家的报价、买家上下文变量集合与商品上下文变量集合。买家在报价的过程中可以通过撒谎来获得更高效用，在这里效用指期望意义下买家得到的商品估值减去该买家的支付价钱。我们考虑可加估值（additive valuation）场景，也即买家对商品集合的估值为该买家对集合内所有商品估值之和。

我们的目标是设计满足占优策略激励相容（dominant strategy incentive compatible, 简称DSIC）和个体理性（individually rational，简称IR）的拍卖机制，并且最大化拍卖者收益。DSIC 指无论其他人如何出价，每个买家真实报价一定能获得最好的效用。IR 指买家真实报价得到的效用不会为负。

03

方 法

我们将上下文拍卖设计问题公式化为一个带限制的优化问题，并进一步转化为一个机器学习问题。首先，我们将机制参数化（我们使用神经网络来对机制进行参数化），并将这些参数作为我们优化问题的自变量。我们将拍卖者的期望收益，也即所有买家的期望支付价格之和作为最大化的目标函数。我们将 DSIC 作为该优化问题的限制条件，这一步可以通过定义后验后悔值然后使用数学语言刻画。IR 条件可以通过机制网络结构的构造得到满足。最后，我们通过从先验分布中采样得到的数据，使用增广拉格朗日乘子法和梯度方法对模型参数进行优化，从而针对具体问题场景自动寻找近似最优的机制。

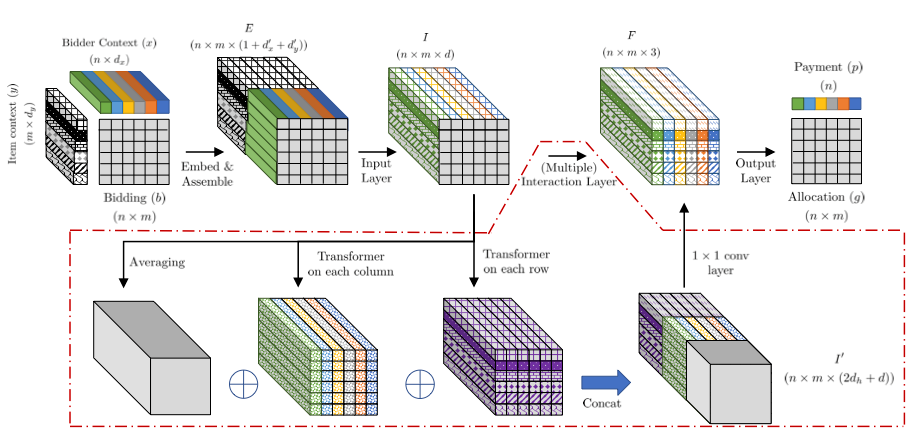
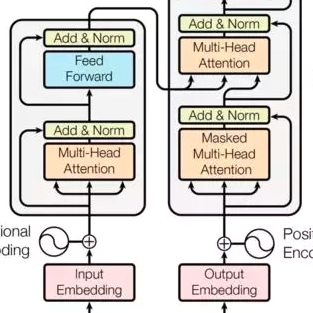
图1. 模型结构

在机制模型设计上，我们设计了 CITransNet 网络结构，如图所示。我们的模型以买家报价、买家上下文与商品上下文这三种信息作为模型输入，先通过输入层来整合每个买家-商品对的报价与上下文信息，然后通过若干个基于 transformer 的交互层来建模所有买家-商品对之间的相互影响，最后通过一个输出层来计算分配结果与支付结果。

04

实 验

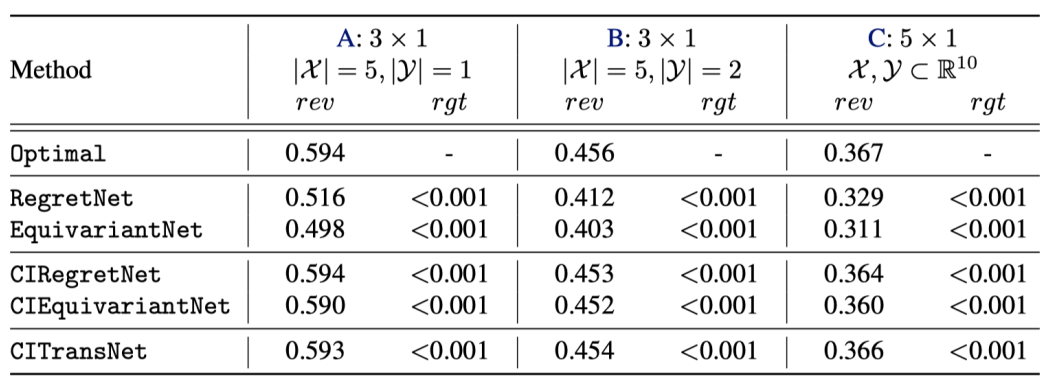
我们分别在单物品与多物品上下文拍卖上进行了实验，实验结果表面我们的方法可以在单物品拍卖上逼近理论最优解，在多物品拍卖上超越已有的基线模型。

图2. 单物品拍卖实验结果

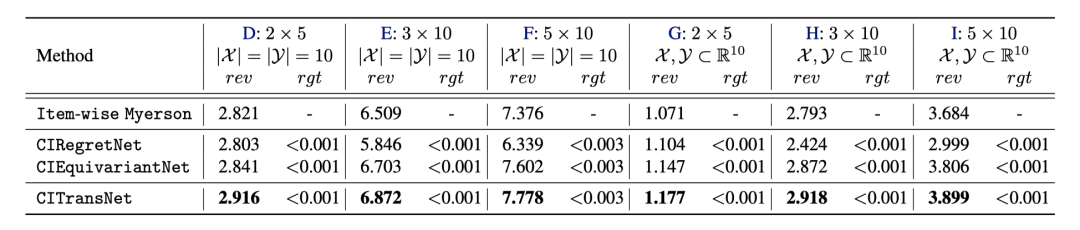
图3. 多物品拍卖实验结果

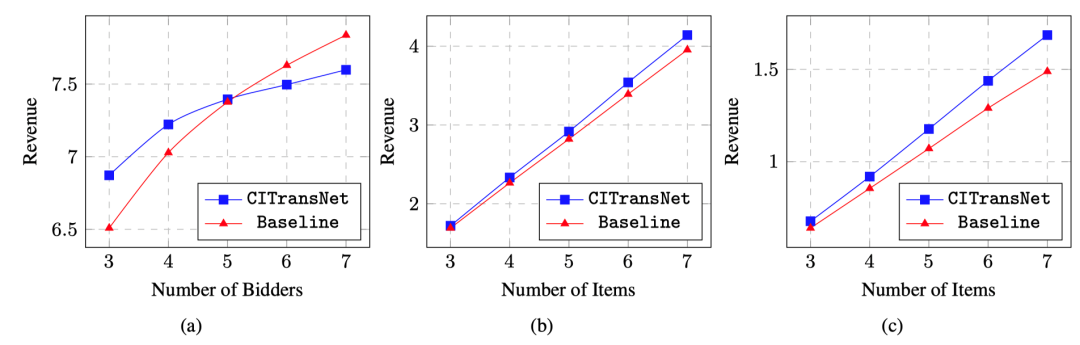
此外，由于我们的模型规模与输入规模无关，因此可以用于跨场景泛化，即在和训练时数量不一样的买家或者商品场景下进行测试。我们发现我们的模型具备一定程度的跨场景泛化能力。

图4. 跨场景泛化实验结果

参考文献

[1] Dütting, Paul, Zhe Feng, Harikrishna Narasimhan, David Parkes, and Sai Srivatsa Ravindranath. "Optimal auctions through deep learning." In International Conference on Machine Learning, pp. 1706-1715. PMLR, 2019. [2] Rahme, Jad, Samy Jelassi, Joan Bruna, and S. Matthew Weinberg. "A permutation-equivariant neural network architecture for auction design." In Proceedings of the AAAI Conference on Artificial Intelligence, vol. 35, no. 6, pp. 5664-5672. 2021. [3] Vaswani, Ashish, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N. Gomez, Łukasz Kaiser, and Illia Polosukhin. "Attention is all you need." Advances in neural information processing systems 30 (2017).