ICML'22| 基于GNN的物理模拟器

2022 年 6 月 25 日 图与推荐

论文地址：https://arxiv.org/pdf/2112.09161.pdf
论文演示地址：https://sites.google.com/view/constraint-based-simulator
欢迎关注小编知乎：戴鸽

DeepMind ICML 2022新作。准确来说是Peter Battaglia 大佬的系列文章中的一个。在较早之前就出过一种专门针对物理仿真的GNN方法，Graph Network，GN[1]。在这个方法基础上衍生出了其他工作，比如与Jure组合作的流体模拟(ICML 2020)[2]，mesh上的模拟(ICLR 2021 Spotlight)[3]，还有之前很出圈的用gnn估计万有引力的工作[4]。另外值得一提的是这套代码采用了JAX框架，说是可以提高效率。可以蹲一波源码开源了。

Introduction

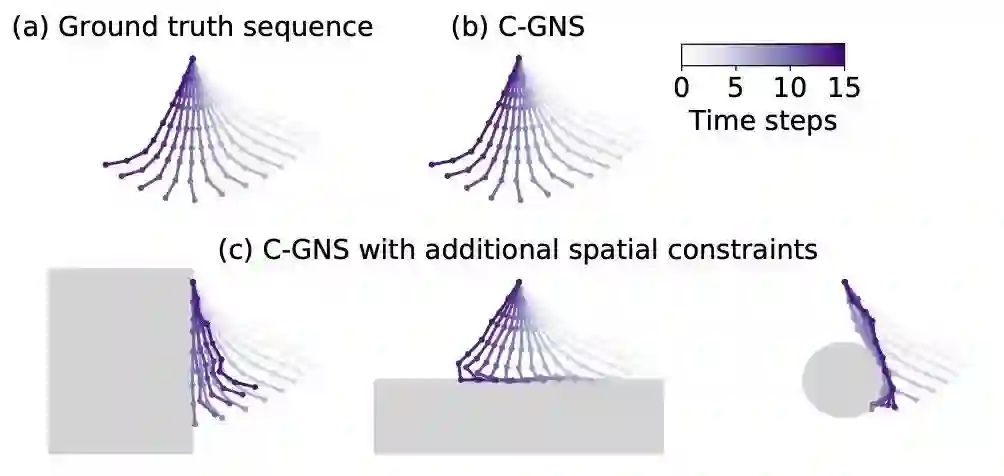
假设用保龄球冲击瓶子，用一种物理的方法解释这个现象，可以构造出两个约束，一个是保龄球和瓶子在空间上不能占据同一位置，另一个是整体的能量与动量必须守恒。这是一种显式的约束条件，能够在整个系统中的局部环境下产生作用。现有方法似乎不太重视这样的约束，因此会导致模拟不出来真实情况。因此，作者提出了带有约束的图网络模拟器，C-GNS来解决这种更复杂的场景。模型整体设计如图所示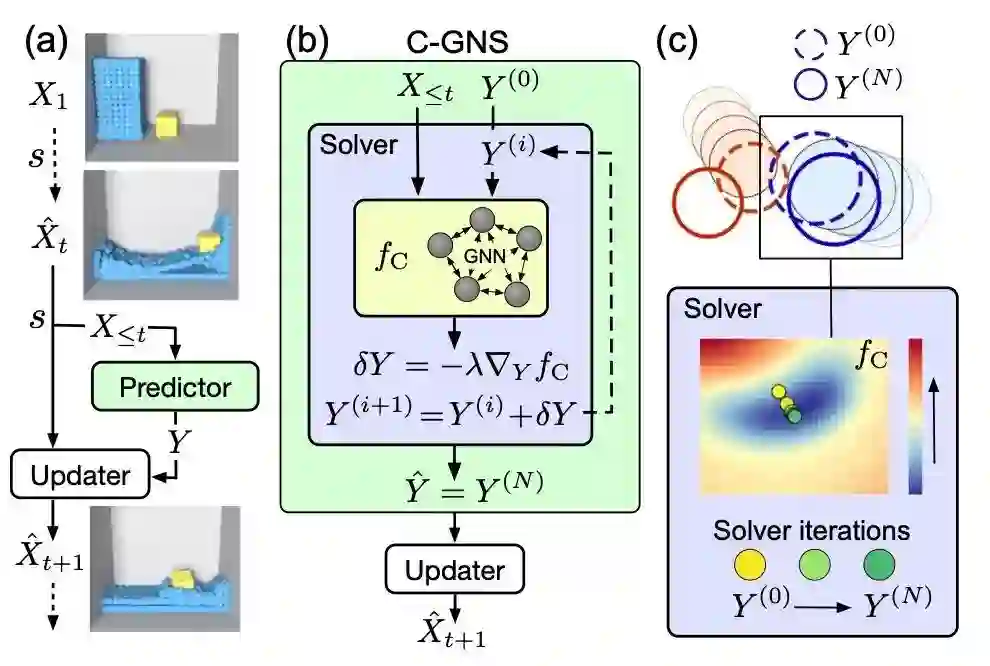：其中，(a)展示了模型描述的物理过程，在一个物理过程中用表示模拟器，节点特征视作 , 表示整个系统的趋势，比较抽象，在不同场景里可以扮演不同角色，比如速度，加速度，可以看做节点的额外特征。因此，一个时间节点下的模拟器应当是利用当前节点信息预测当前系统的趋势。（b）细化了这个模拟器本身的具体流程，传入t之前时刻的节点信息和初始的系统状态，加入一个GNN约束的方程，即可更新整个系统的信息，之后再用系统的信息更新节点信息。(c)中假设了一个简单场景，如果两个小球碰撞，约束器会如何优化。

Method

对于一个描述物理过程的动态场景，点的信息通常依附于时间，如，对于一个物理系统，这个模拟器应当回顾所有历史信息，即$X_{<t}$，记作$\hat{x}_{t+1}=s\left(x_{\leq t}\right)$。虽然在通常情况下我们会考虑马尔科夫链认为一个序列中当前时刻仅受到上一时刻影响，但在物理场景下只靠一个时刻是不能包含这个系统的其他信息的，比如加速度。从显式的角度来看，节点可以确定一个函数，如：节点的前序时间上的位置可以确定新的速度信息，写作$\hat{y}="f_{\mathrm{D}}\left(X_{\leq" t}\right)$。这里的$f_{\mathrm{d}}$就是取一个gnn的前向，这个gnn的边信息表示了两个物体之间是否存在相互作用。在这一系列的物理模拟场景中，这个gnn的选择通常为graph="" network="" block，即gn="" block。系统中的约束主要由$x$本身和反应出的系统趋势$y$共同构成，写作$c="f_{\mathrm{C}}\left(X_{\leq" t},="" y\right)$，$f_{\mathrm{c}}$是一个可训练的网络，并且输出为正数。约束条件首先直接影响y的更新，图（b）中的紫色方框中描述了$y$的第$i$次更新，迭代式写作：<="" p="">

且，这个系统的解为：

至此，完成整个模型的训练，最终的loss函数形式为：

在具体的物理场景里，一个数据集的形式为一个元素j在t时间下有一个位置信息，写作，用表示当前场景的静态环境信息。注意到这种数据集本身是不带速度信息的，所以后期才能用去说明速率的问题。输入的为一组静态信息，为：。速率则是单位时间内位移的变化。在下一时刻中，更新为：

在部分数据集中，就是需要被预测的部分。比如BoxBath数据集，描述模拟水流的一个数据，示意图为：在图网络部分，还需要定义边，如：

所有节点信息，边信息，均应该过一遍MLP，这也符合GN的定义。还有一些其他数据集信息如下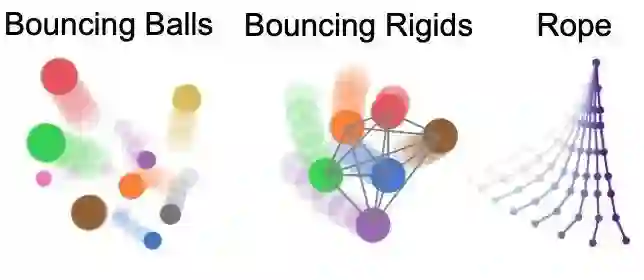：（附录gif，谨慎流量。）

Experiment

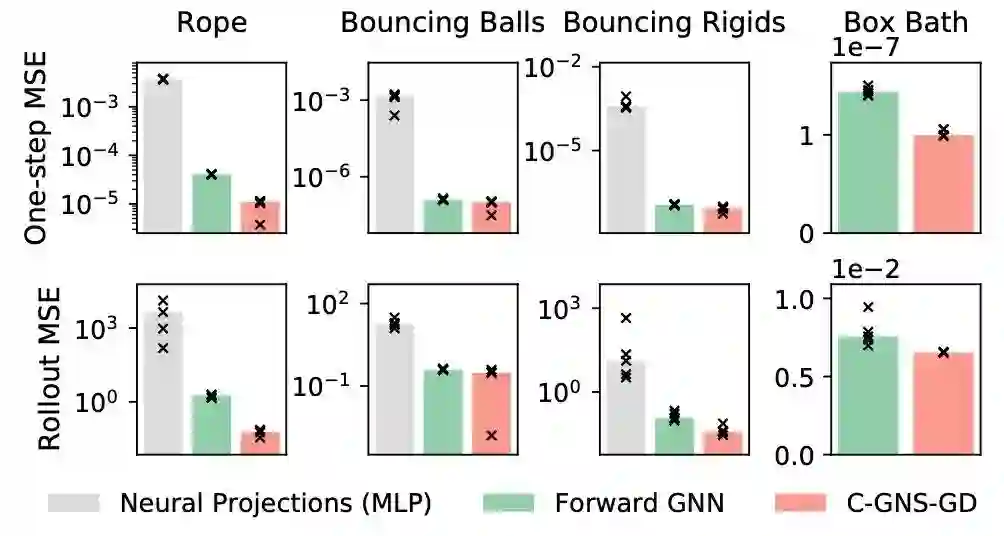
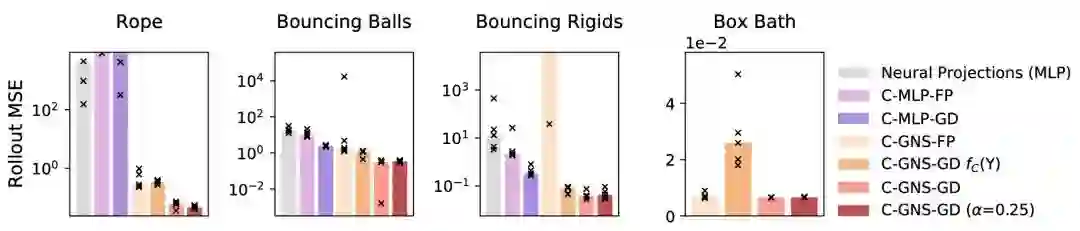
实验表明GNN-based方法会明显优于单纯MLP方法。Forward GNN是仅仅使用GNN部分，其他部分没有优化的方法。这里也展示了更多的消融实验结果：另外，由于本文假设了物体碰撞的优化方式，所以可以在不用重新训练场景的情况下，就能够轻易加入新的障碍物，并且有良好的模拟效果。同样附录展示gif

PS：

肯定有同学会疑惑，如果边的建立是点点之间两两作用，还要算一波mlp，会不会计算消耗特别大。这个问题在之前的工作[2]中的附录里应该可以得到解答。作者认为这个图可以不一定是我们通常的edge index的写法，而是可以转化成CConv（Continue Convoluion），或者说一种CNN的形式，最终只需要单卡v100就能训练。具体情况有兴趣的同学可以自行观看。

[1] Battaglia P W, Hamrick J B, Bapst V, et al. Relational inductive biases, deep learning, and graph networks[J]. arXiv preprint arXiv:1806.01261, 2018. [2] Sanchez-Gonzalez A, Godwin J, Pfaff T, et al. Learning to simulate complex physics with graph networks[C]//International Conference on Machine Learning. PMLR, 2020: 8459-8468. [3] Pfaff T, Fortunato M, Sanchez-Gonzalez A, et al. Learning mesh-based simulation with graph networks[J]. arXiv preprint arXiv:2010.03409, 2020. [4] Lemos P, Jeffrey N, Cranmer M, et al. Rediscovering orbital mechanics with machine learning[J]. arXiv preprint arXiv:2202.02306, 2022.

登录查看更多