【第一个对抗性博弈的系统性概述】《对抗性博弈决策研究综述》同济大学2022最新综述

到目前为止，博弈论已经在各个领域形成了大量应用，包括经济学、工业、法学和人工智能，其中每个玩家只关心自己的利益，以非合作或合作的方式，但对其他玩家没有明显恶意。然而，在很多实际应用中，如扑克、国际象棋、追逃、缉毒、海岸警卫队、网络安全和国防等，玩家往往有明显的敌对立场，即每个玩家的自私行为不可避免地或有意地对其他玩家造成损失或破坏。按照这一思路，本文从一系列角度对对抗性博弈中广泛采用的三种主要博弈模型，即零和范式和广泛形式博弈、斯塔尔伯格博弈（安全）博弈、零和微分博弈进行了系统的调查，包括博弈模型的基本知识、（近似）均衡概念、问题分类、研究前沿、（近似）最优策略寻求技术、流行算法和实际应用。最后，还讨论了相关对抗性博弈的未来研究方向。

索引词：对抗博弈，零和博弈，斯塔尔伯格博弈，微分博弈，纳什均衡。

I. 前言

自John von Neumann, John Nash等人的开创性工作[1]-[3]以来，博弈论一直是一个强大而传统的范式，用于模拟一群玩家之间复杂而智能的互动，并改善自私的玩家的决策。迄今为止，它已经在各种领域发现了广泛的现实应用，包括经济学、生物学、金融学、计算机科学、政治学等等，其中每个参与者只关心自己的利益[4]-[6]。即使在60年代的冷战期间，它也发挥了极其重要的作用，并被许多国家的国防机构采用，如美国的安全控制机构[7]。

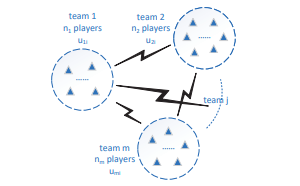
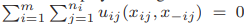
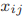
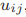
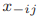
图1. 一个具有同时或连续行动、完全或不完全信息、对称或不对称信息的对抗博弈的一般框架，其中三角形表示玩家，存在m个团队，在团队内部，团队成员以合作方式进行博弈，而团队之间的博弈是对抗性的，通常是零和，即 为所有策略，下标ij代表第i队中的第j个玩家，其策略和效用函数分别表示为和。而是除第i队中第j名球员外的所有球员的策略情况。

对抗性博弈是一类特别重要的博弈模型，博弈者故意与对方竞争，同时实现自己的效用最大化。迄今为止，对抗性博弈已经成为众多现实应用中塑造高效决策的正统框架，如扑克、国际象棋、追逃、缉毒、海岸警卫、网络安全和国防等。例如，在德州扑克中，它一直是由AAAI等国际知名会议举办的测试研究人员提出的博弈论和人工智能（AI）算法的主要比赛之一，多个玩家相互竞争，通过寻求复杂的策略技术来赢得比赛[8]。一般来说，对抗性博弈具有以下几个主要特点：1）在有限的计算资源和/或样本的情况下，高效快速的算法设计很难；2）许多实际问题的信息不完善，也就是说，有些信息对一个或多个玩家是私有的，但对其他玩家是隐藏的，如扑克牌游戏。3）大型模型，包括大型行动空间和信息集，例如，道路网络安全问题中的对手空间是1018的数量级[9]；4）众多现实生活应用中的不完全信息，即一个或多个智能体不知道正在进行什么游戏（如 g., 在这种情况下，正在进行的游戏一般用玩家的不确定性来表示，如具有不确定参数的不确定报酬函数；5）可能的动态特征，即所进行的游戏有时是时间变化的，而不是静态的，例如，一个偷猎者在野生动物公园里可能有不同的偷猎策略，因为环境随季节而变化。值得指出的是，这里的不完全信息与不完全信息是截然不同的，正如一些研究者所区分的那样，尽管它们在一些文献中被互换使用。此外，其他可能的特征包括有界理性，玩家可能不完全理性，比如恐怖分子任意随机的独狼式攻击。然而，值得注意的是，并不是所有的对抗性博弈都具有不完美和/或不完全的信息，例如，围棋游戏既有完美的信息，也有完全的信息，因为它有明确的游戏规则，所有棋子的位置对双方来说在任何时候都是可见的，也有对手的行动，著名的人工智能agent，如AlphaGo和AlphaZero[10]-[12]已经很好地解决了这个问题。

由于竞争特征在大量现实世界的应用中无处不在，直到现在，对抗性博弈已经得到了广泛的研究[13]-[18]。例如，作者在[13]中对2018年Stackelberg安全博弈（SSG）的技术进展进行了广泛的调查，作者在[14]中回顾了一些主要的基于反事实后悔最小化（CFR）方法的不完美信息的广泛形式博弈的纳什均衡（NE）计算算法。作者在[15]中回顾了博弈论和优化算法的结合使用，并对该领域的研究进行了新的分类，作者在[16]中回顾了分布式在线优化，从隐私保护机制角度的联合优化，以及从两个方面的合作/非合作游戏，即, 作者在[17]中从问题分类、性能指标、最先进的性能结果和未来潜在的研究方向的角度，调查了分布式在线学习的最新进展，包括分布式在线优化和在线游戏。此外，考虑到博弈论在国防中的重要性，[18]、[19]对博弈论在国防中的应用进行了一些回顾，[20]对基于博弈论和机器学习（ML）方法的防御性欺骗进行了调查。尽管如此，仍然缺乏从基本模型知识、均衡概念、最优策略寻求技术、研究前沿和流行算法等角度对对抗性博弈的彻底概述。

在上述事实的激励下，本调查旨在从多个维度对对抗性博弈进行系统回顾，包括对抗性博弈中经常采用的三种主要模型（即零和范式和广泛形式博弈、Stackelberg（安全）博弈和零和差分博弈）的模型、（近似）最优策略概念（即：NE、相关均衡、coarsecorrelated均衡、强Stackelberg均衡、teammaxmin均衡以及相应的近似概念），（近似）最优策略计算技术（如CFR方法、AI方法），最先进的结果、流行的算法、潜在的应用以及有希望的未来研究方向。据我们所知，本综述报告是第一个关于对抗性博弈的系统性概述，一般来说，它为上述调查报告提供了一个正交和补充的部分，这可能有助于相关领域的研究人员和从业人员。请注意，这三种博弈模型并不相互排斥，但对于同一博弈，从不同的角度看，可能会有重叠。例如，Stackelberg博弈和差分博弈也可以是零点博弈，等等。此外，实际上还存在其他借助于对抗性博弈的模型，如贝叶斯博弈、马尔科夫博弈（或随机博弈）、信号博弈、行为博弈论和进化博弈论。然而，我们并不打算在这次调查中回顾所有这些模型，因为它们中的每一个都具有独立的意义，并且在现有的各种材料中相当丰富。

本调查的结构安排如下。第二节介绍了详细的博弈模型和解决方案的概念，第三节回顾了现有的主要文献和最先进的结果，第四节阐述了一些流行的算法，第五节介绍了一系列的应用，第六节讨论了有前途的未来研究方向，最后在第七节得出结论。