「人机对抗中的博弈学习方法」最新2022综述

近年来，人机对抗智能技术作为人工智能领域的前沿方向取得了一系列突破性的进展，如 AlphaGo 和 DeepStack 分别在围棋和二人无限注德州扑克中击败了人类专业选手. 这些突破离不开博弈论和机器学 习的深度结合. 本文通过梳理当前人机对抗智能技术领域的重要工作，深入分析博弈论和机器学习在其中 发挥的作用，总结了面向人机对抗任务的博弈学习研究框架，指出博弈论为人机对抗任务提供博弈模型和 定义求解目标，机器学习帮助形成稳定高效可扩展的求解算法. 具体地，本文首先介绍了人机对抗中的博 弈学习方法的内涵，详细阐述了面向人机对抗任务的博弈学习研究框架，包括博弈模型构建、解概念定义、 博弈解计算三个基本步骤，之后利用该框架分析了当前人机对抗智能技术领域的典型进展，最后指出了人 机对抗中的博弈学习未来发展可能面临的挑战. 本文梳理总结的人机对抗中的博弈学习研究框架为人机对 抗智能技术领域的发展提供了方法保障和技术途径，同时也为通用人工智能的发展提供了新思路.周雷，尹奇跃，黄凯奇. “人机对抗中的博弈学习方法”, 计算机学报，2022.(https://cjc.ict.ac.cn/online/bfpub/zl-2022323165812.pdf)

1 引言

人机对抗智能技术研究计算机博弈中机器战 胜人类的方法，是当前人工智能研究领域的前沿方 向，它以人机（人类与机器）和机机（机器与机器） 对抗为主要形式研究不同博弈场景下，机器智能战 胜人类智能的基础理论与方法技术[1] . 人机对抗智 能技术通过人、机、环境之间的博弈对抗和交互学 习，探索巨复杂、高动态、不确定的对抗环境下机 器智能快速增长的机理和途径，以期最终达到或者 超越人类智能.

人机对抗智能技术的突破离不开机器学习的 发展，机器学习主要研究如何让机器通过与数据的 交互实现能力的提升[2][3] . 然而，与传统的机器学习 关注单智能体（single-agent）与环境的交互不同， 人机对抗智能技术研究的场景往往包含两个或两 个以上智能体，也就是多智能体（multi-agent）的 情形，这些智能体都拥有自己的优化目标，比如最大化自身收益. 此时，如果直接应用单智能体机器 学习方法，得到的智能体（称为中心智能体）一般 表现欠佳[4][5] . 这是因为传统机器学习方法假设数 据的产生机制是平稳的（stationary）[6]（即数据均 来自于同一个分布，简称为环境的平稳性），这一 假设忽略了研究场景中的其他智能体，而这些智能体也同时在进行学习，因此其行为模式会随着时间 发生变化，从而破坏中心智能体所处环境的平稳 性，进而导致传统机器学习方法失去理论保证[2][3] . 更为严峻的是，随着人机对抗场景中智能体数量的 增加，环境非平稳的问题将会愈发凸显，多个趋利 的智能体在学习的过程中相互影响的情况将不可 避免.

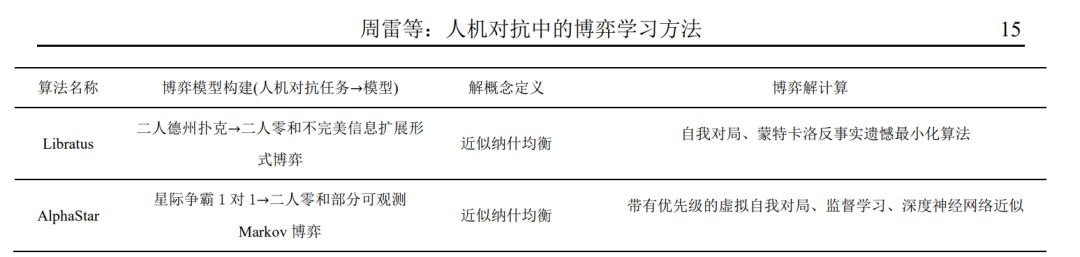
为了处理环境非平稳的问题，有学者考虑将博 弈论引入机器学习方法中[7] . 这主要是因为博弈论 本身就是为了研究多个利己个体之间的策略性交 互（strategic interactions）而发展的数学理论. 博弈 论诞生于 1944 年 von Neumann 和 Morgenstern 合著 的 Theory of Games and Economic Behavior[8] . 在完 全理性的假设下，博弈论给出了一系列解概念来预 测博弈最终可能的结果. 博弈论早期的大部分工作关注不同博弈场景下解概念（solution concepts）的 定义、精炼（refinement）、存在性及其拥有的性质 [9] . 随着博弈论的发展，部分研究者开始研究在非 完全理性的情形下，个体是否可以通过迭代学习的 方式来达到这些解概念，其中著名的工作包括 Brown 提出的虚拟对局（fictitious play）[10]，Hannan 和 Blackwell 研究的无悔学习（no-regret learning， regret minimization，or Hannan consistency）[11][12][13] 等. 近年来，得益于机器算力的提升和深度学习的 兴起，人机对抗智能技术领域取得了一系列突破， 如 DeepMind 团队开发的 AlphaGo[14]首次击败了人 类围棋顶尖选手李世石，阿尔伯塔大学团队开发的 DeepStack[15]在二人无限注德州扑克中击败了专家 级人类选手等. 在 AlphaGo 中，围棋被建模为二人 零和完美信息扩展形式博弈，并利用自我对局、蒙 特卡洛树搜索以及深度神经网络近似来对博弈进 行求解；在 DeepStack 中，二人德州扑克被建模为 二人零和非完美信息扩展形式博弈，求解方法结合 了自我对局、反事实遗憾最小化算法以及深度神经 网络近似. 从这些例子可以看出，人机对抗智能技 术领域的突破离不开博弈论和机器学习的深度结合.

然而，虽然人机对抗智能技术领域目前取得了 一系列突破，博弈论与机器学习交叉方向的研究却 缺乏清晰的研究框架. 基于此，本文通过梳理人机 对抗智能技术领域的重要工作，介绍了人机对抗中 的博弈学习方法的内涵，总结了面向人机对抗任务 的博弈学习研究框架，包括其组成要素和基本步 骤，并利用该框架对人机对抗智能技术领域的典型 进展进行了分析. 本文作者认为，随着人机对抗智 能技术领域试验场景和测试环境逐渐接近真实场 景，场景的复杂性和对抗性急剧增加，结合现代机 器学习方法和博弈论的博弈学习方法将会在未来 人机对抗领域的发展中发挥越来越重要的作用。

2 发展历史

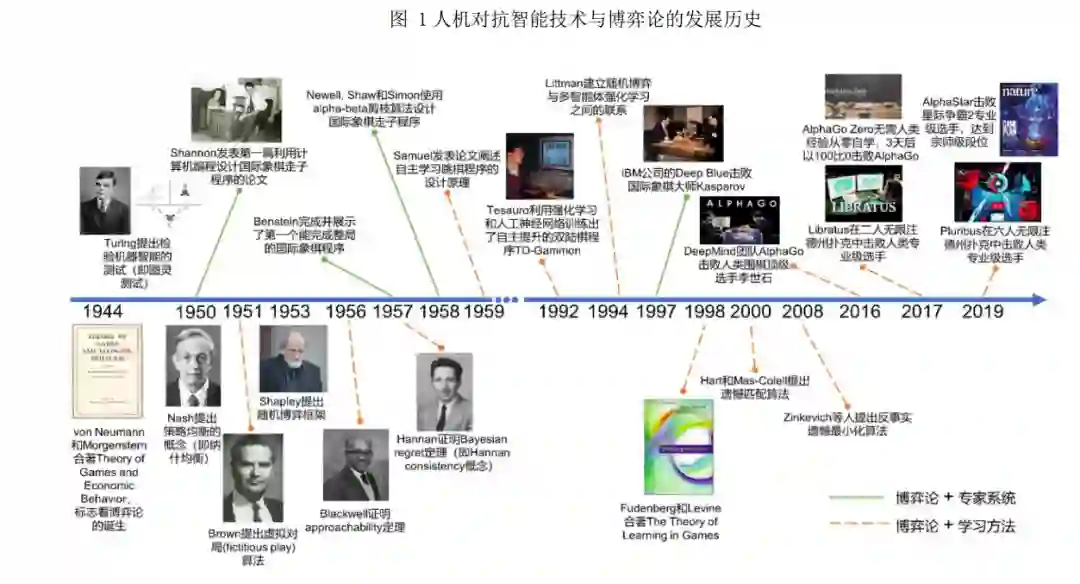
自图灵测试这一人机对抗模式在 1950 年被提 出[16]以来，博弈论和机器学习就在人工智能的发展 中发挥着越来越重要的作用，并呈现出交叉融合的 趋势. 本文梳理了人机对抗智能技术和博弈论领域 开创性的工作和里程碑事件，并将其发展历史分为 两条路线，一条是博弈论结合专家系统（见图 1 中 绿色实线），另一条是博弈论结合学习方法（见图 1 中橙色虚线）.

1.1 路线一：博弈论结合专家系统

在发展路线一中，为了取得较好的人机对抗表 现，研究者们主要是针对基于博弈论的 min-max 树 搜索算法进行优化，并结合专家经验来改进评估函 数. 路线一的简要发展历程如下: 1950年Shannon发表了第一篇利用编程来实现 国际象棋走子程序的论文[17]，论文中 Shannon 参考 von Neumann 证明的 minimax 定理[8][18]设计了 min-max 搜索算法和局面评估函数. 对于局面评估 函数的设计，参考的是如下定理：在国际象棋中， 最终的结局只可能是以下三种当中的一种：(1) 不 论白方如何走子，黑方有一种策略总能保证赢；(2) 不论黑方如何走子，白方有一种策略总能保证赢； (3)黑白双方都有一种策略保证至少平局. 1956 年 Samuel 利用第一台商用计算机 IBM 701 编写了跳棋（checkers）走子程序，并在 1959 年发表论文总结了该程序的设计思想和原理[19] . 该 跳棋走子程序使用了 min-max 搜索. 1957 年，Bernstein 带领的团队在 IBM 701 上 完成了第一个能下完整局的国际象棋走子程序，该程序使用了 min-max 搜索，但每次最多向后搜索 4 步，每步只能考虑 7 个备选走法. 1958 年，Newell，Shaw 和 Simon 第一次在国 际象棋程序中使用 alpha-beta 剪枝搜索算法[20] . Alpha-beta 剪枝算法是 min-max 搜索算法的改进， 通过剪掉明显次优的子树分支，该算法极大地降低 了搜索空间. 该算法最初由 McCarthy 在 1956 年提 出. 此后，跳棋和国际象棋程序的优化大多围绕评 估函数和搜索算法进行改进. 随着计算能力的增 强，IBM 公司开发的国际象棋程序 Deep Blue 在 1997 年利用总结了大量人类经验的评估函数和强 大的搜索能力击败国际象棋大师 Kasparov，一时轰 动. 该事件从此成为人机对抗智能技术发展历史上 的标志性事件.

1.2 路线二：博弈论结合学习方法

路线一中采用的方法很难称得上实现了机器 的―学习‖能力，在路线二中，研究者们试图克服机 器对专家数据的过度依赖，希望能够打造自主学习 的智能机器. 路线二的简要发展历程如下： 最早在人机对抗研究中引入学习的是 Samuel， 他 1957 年 完 成 的 跳 棋 走 子 程 序 不 仅 使 用 了 min-max 搜索，同时也引入了两种―学习‖机制[19]： 死记硬背式学习（rote learning）和泛化式学习 （learning by generalization）. 前者通过存储之前下 棋过程中计算得到的局面得分来减少不必要的搜 索，后者则根据下棋的不同结果来更新评估函数中 不同参数的系数来得到一个更好的评估函数. 此 外，该论文也第一次提到了自我对局（self-play）. 此 后，这种通过学习来提升机器能力的思想就一直没 能引起重视. 直到 1990 年前后，才陆续出现了能够 学习的棋类程序. 这其中比较知名的是 1994 年 Tesauro 结合神经网络和强化学习训练出的双陆棋 程序 TD-Gammon[21] . TD-Gammon 的成功引起了许多学者对学习算 法的兴趣，并促成了博弈论与机器学习的初步结 合，其中著名的工作是 Littman 在 1994 年正式建立 了 Markov 博弈（或随机博弈）与多智能体强化学 习之间的联系. 之后，Markov 博弈便作为多智能体 强化学习的理论框架，启发了众多学者的研究. 同 时，在该论文中 Littman 也提出了第一个多智能体 强化学习算法 minimax-Q [22]. Minimax-Q 是针对二 人零和博弈的学习算法，当博弈的双方都使用该算 法时，最终博弈双方的策略都会收敛到二人零和博 弈的最优解极大极小策略上. 值得指出的是，除了人工智能领域，博弈论领 域的研究者们很早也开始了对学习方法的研究.与 人工智能领域学者的出发点不同，他们关注的是在 博弈模型给定的情形下，如何设计迭代学习的规则 能使个体的策略收敛到均衡.此类方法之后被称为 博弈学习（game-theoretic learning）方法.博弈学习 方法的思想最早可以追溯到 1951 年 Brown 提出的 虚拟对局（fictitious play）[10]，即采用迭代学习的 方式来计算二人零和博弈的极大极小策略，之后著 名 的 博 弈 学 习 方 法 包 括 无 悔 学 习 （ no-regret learning ） [11][12][13] 和 复 制 动 力 学 （ replicator dynamics）[23] . 在 1998 年，几乎与 Littman 等人同 一时期，Fundenberg 和 Levine 出版了著作 The Theory of Learning in Games[24]，对之前博弈学习方 法的研究进行了汇总、总结和扩展.博弈学习方法的 研究为博弈论中的解概念（主要是纳什均衡）提供 了非理性假设下的解释，换言之，非理性的个体在 一定学习规则的指导下也能达到均衡. 此后，博弈论和机器学习领域的研究兴趣和研 究内容开始交叉，逐步形成了博弈论与机器学习结 合的博弈学习方法[25][26][27][28][29][30] .相关工作包括： (1) 利 用 强 化 学 习 方 法 计 算 博 弈 的 解 ， 比 如 Nash-Q [31]等；(2)利用博弈论中的学习方法进行游戏 AI 的算法设计，比如针对不完美信息博弈的反事实 遗憾最小化算法[28]（属于无悔学习算法的一种）； (3)利用机器学习加强博弈论中学习方法的可扩展 性，比如虚拟自我对局（fictitious self-play，FSP） [29] . 相比于传统解决单智能体与环境交互问题的机 器学习方法，与博弈论结合的学习方法有两个优 势：一是充分考虑了多个智能体同时最大化收益时 环境的非平稳问题，学习的目标是任务的均衡解而 不是让某个智能体的收益最大化；二是在满足模型 的假设时，这些算法一般具有收敛的理论保证.特别 地，面向人机对抗任务，人机对抗中的博弈学习方 法在此基础上添加了人机对抗任务建模，为的是能 更好地利用和拓展现有的博弈学习方法来处理复 杂的人机对抗任务.

近年来，随着深度学习的兴起，深度神经网络 被广泛应用于人机对抗任务,形成了一系列优秀的 模型和博弈学习算法[5][32][33][34][35][36][37][38][39][40] . 这 也促进了人机对抗智能技术近期一系列的突破，包 括2016 年AlphaGo击败围棋9段选手李世石，2017 年 Libratus[30]和 DeepStack[15]分别在二人无限注德州扑克中击败人类专业选手以及 2019 年 AlphaStar[41]在星际争霸 2 中击败人类顶级选手.

3 人机对抗中的博弈学习方法内涵

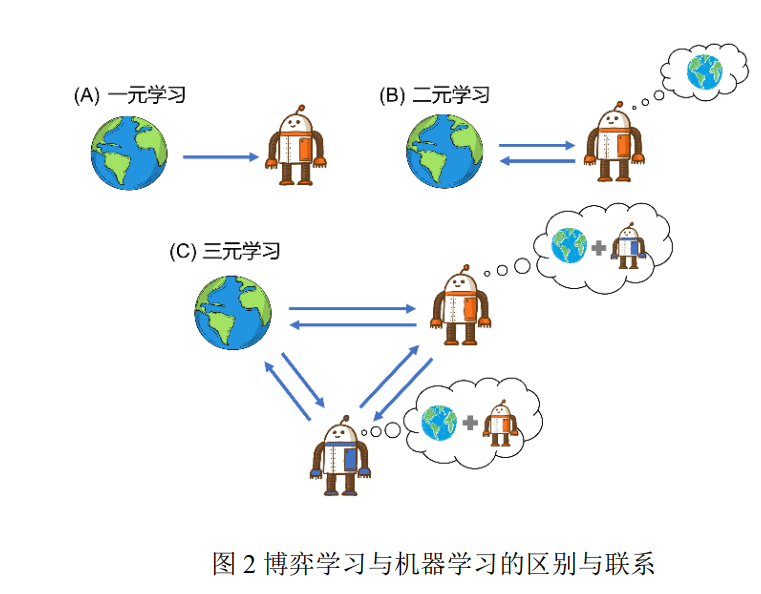
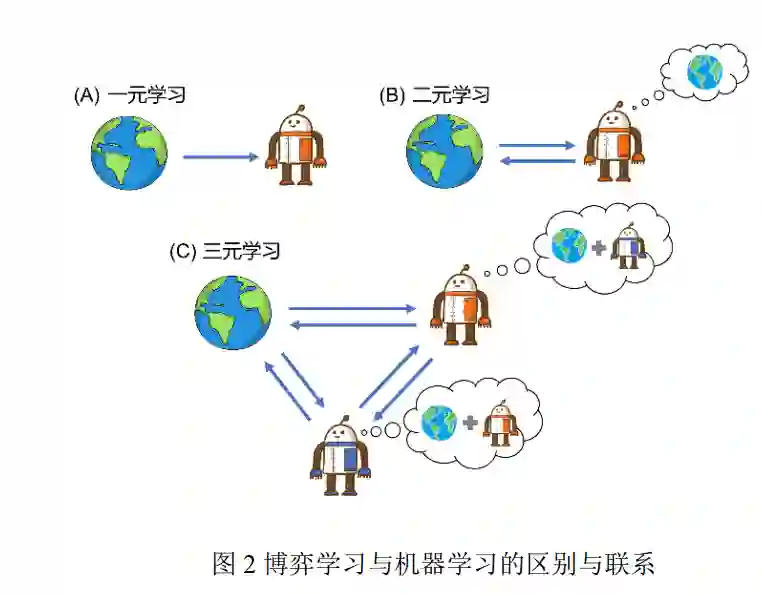
人机对抗中的博弈学习方法是一种面向人机 对抗任务，以博弈论为理论基础、以机器学习为主 要技术手段，通过智能体与环境、智能体与其他智 能体的交互来获得具有良好性质（比如适应性、鲁 棒性等等）博弈策略的学习方法，是实现人机对抗 智能技术的核心. 具体地，人机对抗中的博弈学习 方法基于博弈论建模人机对抗任务和定义学习目 标，并利用机器学习方法来帮助设计高效、稳健、 可扩展的学习算法以完成人机对抗任务. 为了阐述博弈学习方法与当前机器学习方法 的区别与联系，本文按照系统中信息的流向以及信 息产生的机制将已有的学习框架划分为一元、二元 以及三元（或多元）学习. 在一元学习中，智能体 从数据中获取知识，并且这个过程只涉及数据到智 能体的单向信息流动，监督学习、无监督学习以及 深度学习都属于一元学习（见图 2 (A)）. 在二元学 习中，智能体通过与环境互动得到数据，进而获取 知识，与一元学习不同的是此时数据的产生不仅取 决于环境也取决于智能体，即智能体决策的好坏影 响它自身学习的效果，必要时智能体还需要对环境 动力学进行建模，单智能体强化学习属于二元学习 （见图 2 (B)）. 在三元学习中，智能体通过与环境 和其他智能体的交互获得数据，此时智能体学习的 效果受到环境和其他智能体的共同影响，必要时智 能体需要对环境动力学和其他智能体进行建模（见 图 2 (C)），博弈学习属于三元学习.

4 人机对抗中的博弈学习研究框架

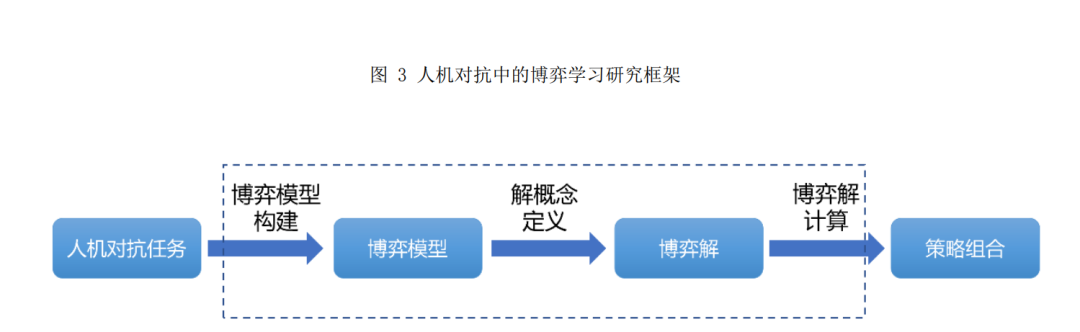
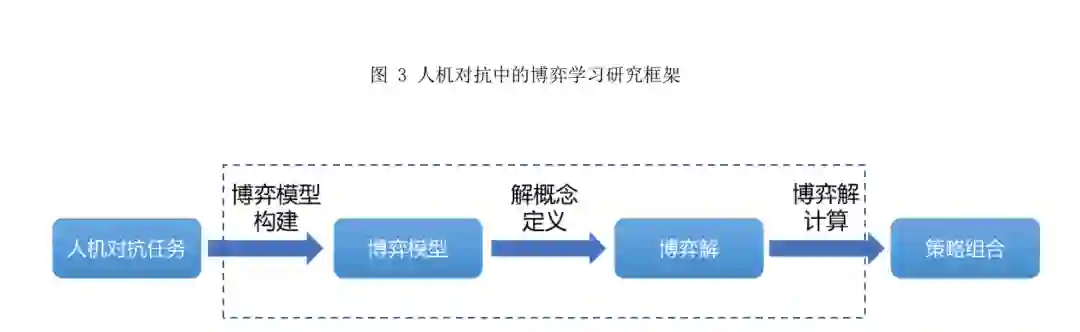
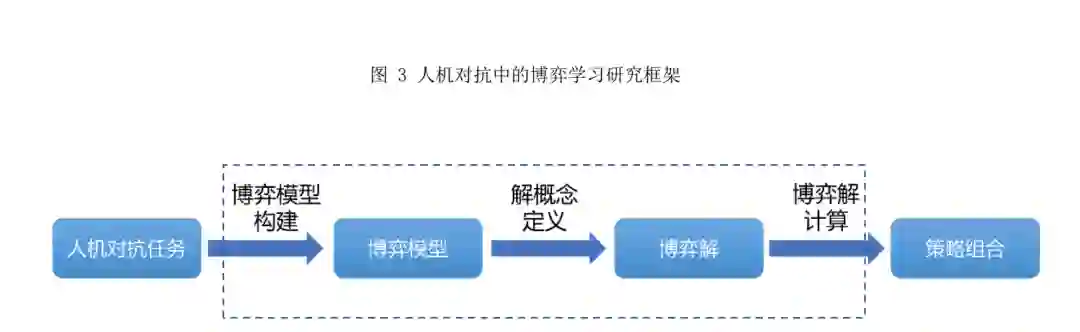
通过对博弈论和人机对抗智能技术发展历程 的梳理，并结合人机对抗中的博弈学习方法的内 涵，本文总结出了如图 3 所示的人机对抗中的博弈 学习研究框架：人机对抗中的博弈学习研究框架以 人机对抗任务为输入，首先通过博弈模型构建获得博弈模型，然后通过解概念定义得到博弈的可行 解，最后通过博弈解计算输出满足需求的博弈策略 组合，也就是学习任务的解. 直观来讲，人机对抗 中的博弈学习研究框架将一类人机对抗任务的解 决近似或等价转换为对某一类博弈问题的求解，该 框架包含两个组成要素（博弈模型和博弈解）和三 个基本步骤（博弈模型构建、解概念定义和博弈解 计算）.

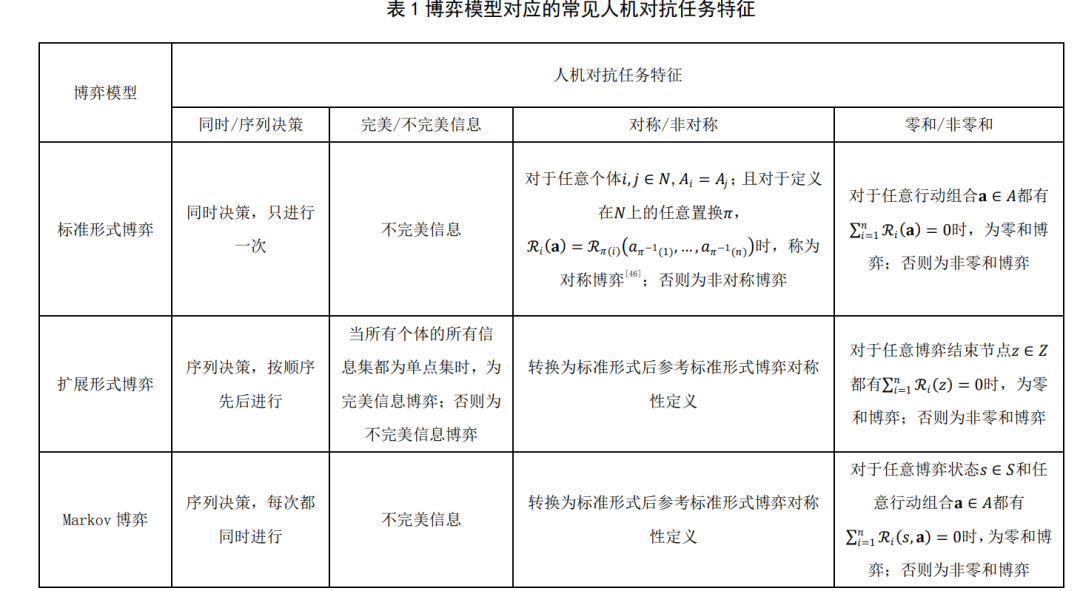
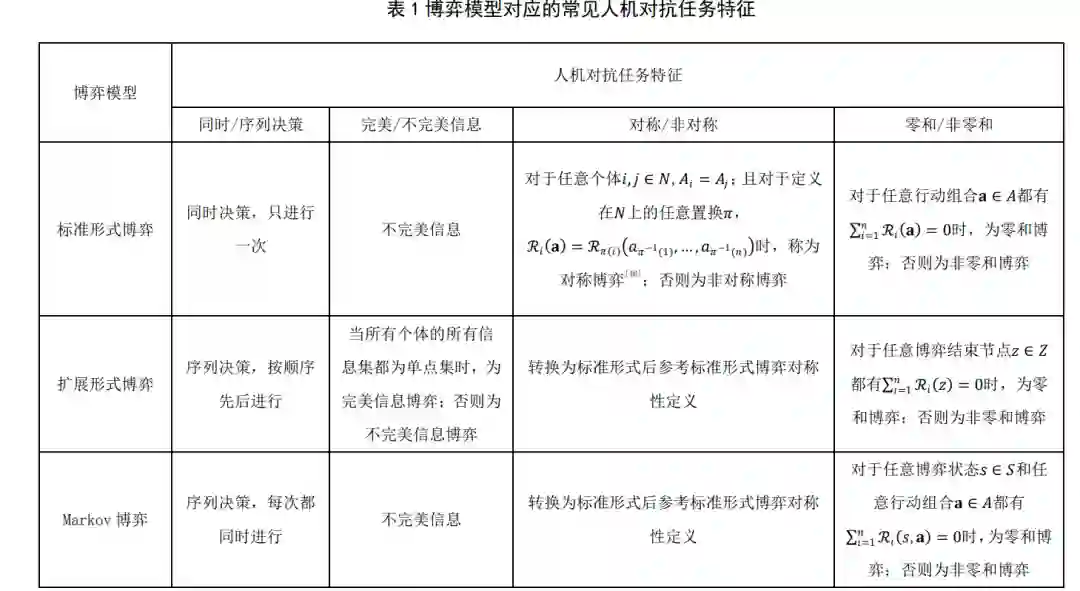
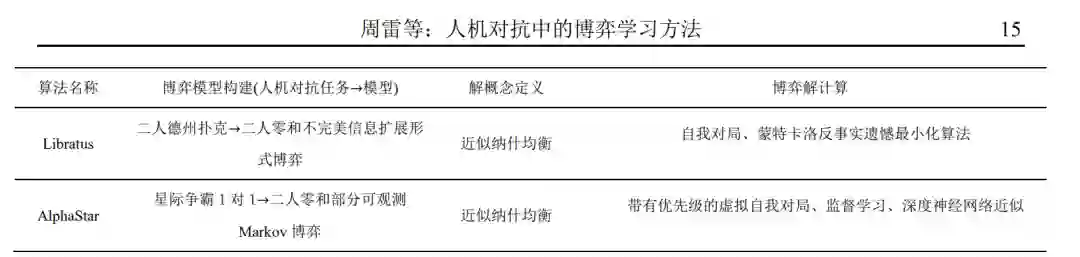
5 典型应用上一节阐述了人机对抗中的博弈学习研究框 架，本节将利用该框架对当前人机对抗智能技术领 域的重要工作进行分析（如表 2 所示），这些工作 基本涵盖了本文介绍的几种博弈模型，包括完美信 息扩展形式博弈（围棋）、不完美信息扩展形式博 弈（德州扑克）以及部分可观测 Markov 博弈（星 际争霸 2）. 各工作的具体分析如下：

6 总结与展望

人机对抗智能技术是人工智能发展的前沿方 向，它通过人、机、环境之间的博弈对抗和交互 学习研究机器智能快速提升的基础理论与方法技 术. 为了更好地促进人机对抗智能技术的发展， 本文通过梳理人机对抗智能技术领域的重要工作， 总结了面向人机对抗任务的博弈学习研究框架， 指出了博弈论和机器学习在其中发挥的作用，阐 述了人机对抗中的博弈学习方法的两个组成要素 和三个基本步骤，并利用该框架分析了领域内的 重要进展. 与此同时，本文就当前人机对抗中的 博弈学习方法面临的理论和应用难点问题进行了 介绍，包括非零和博弈求解目标定义、博弈学习 方法的可解释性、多样化博弈学习测试环境构建 以及大规模复杂博弈快速求解. 人机对抗中的博 弈学习方法是人机对抗智能技术的核心，它为人 机对抗智能技术领域的发展提供了方法保障和技 术途径，同时也为通用人工智能的发展提供了新 思路.