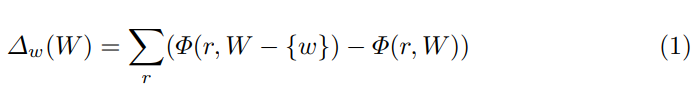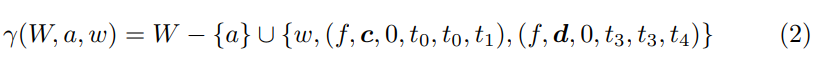《战斗模拟的自动火力支援规划》美海军

如今的建设性战斗模拟不能自动生成现实的战斗计划。造成这种情况的一个原因是缺乏一个火力支援规划算法来支持一个给定的机动计划。我们提出了一种对火力支援规划问题进行建模的方法，假定有一个战术风险的数字定义。解决方案的空间似乎很难穷尽搜索，因此提供了一种火力支援规划算法，该算法可以在多项式时间内产生一个合理的、尽管是次优的计划。

问题定义

我们用单元（unit）这个词来指任何由一个或多个模拟战斗人员组成的团体，他们作为一个单一的编队一起移动和战斗。一个单元的移动是按照路线进行的，而路线是由一系列的航点或三维空间中的位置定义的。单元沿着地表以现实的、已知地形类型的速度向他们的下一个节点直线行进。在这个问题上，有任务的机动部队的路线是预先确定的和固定的。没有任务的机动部队被认为是火力支援部队。

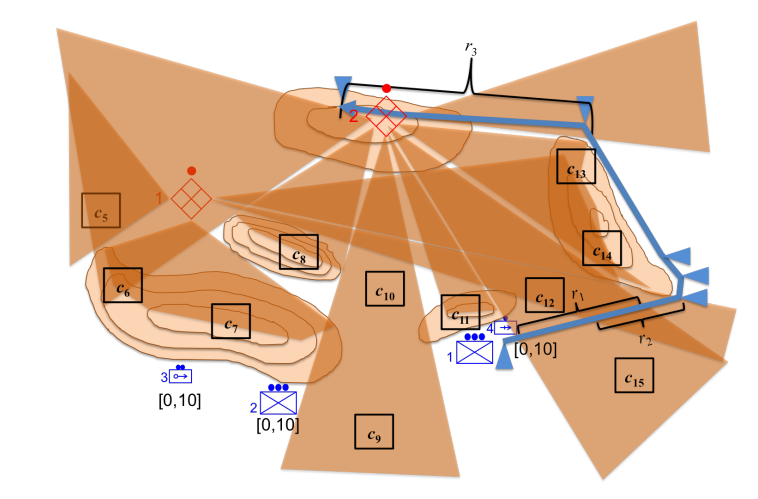
图1. 友军单位1的任务是遵循一条由六个节点组成的路线，用三角形标记。敌方单位1（菱形符号）可以在风险段r2期间损害友方单位1。敌方单位2在r1和r3期间可以损害它。[0,10]标记表示火力支援资源的可用间隔，标有ci的方框是可能的火力支援地点。两者都将在下文中描述。

• 应用火力支援任务

• 火力支援资源

贪心算法

我们提供以下贪心算法来生成一个火力支援计划。当然，鉴于上述优化和满足的解释，它既不是最优的也不是完整的，但它可以有效地产生一个合理的计划。

对于每个资源，该算法在其搜索边界（N和M集）上保持着压制每个敌人单位的任务。在每次通过主循环时，它选择N∪M中最能降低总风险的任务。为了限制复杂性，不需要移动的潜在任务（N中的任务）被优先考虑。每当一个任务w被添加到当前计划W中时，我们就从N和M中删除w的所有兄弟姐妹，这些兄弟姐妹是由相同的可用任务产生的。然后，我们从γ给出的新的（更短的）可用性任务中为N和M生成新的选项。

当总风险足够小或没有任务选择时，该算法就会终止。如果我们假设火力支援任务有一个最小的有用持续时间，例如发射一发子弹的时间，那么每次选择任务都会移除一个持续时间为t的资源，并用两个持续时间之和为t-或更小的资源取代它。由于所有资源持续时间的总和至少在每个循环迭代中减少，我们最终将得到一个小于的总和，这只有在边界没有任务，终止执行时才可能是真的。