《无人机蜂群防御策略的行动规划和优化》2022.12最新97页论文

这篇论文考虑的情况是，一架无人机保卫一个高价值的目标，以抵御一些入境的攻击无人机。防御性无人机配备了短程武器，必须以最有效的方式摧毁每一架攻击性无人机。这个问题是应用数学中几个开放性问题的交汇点，例如在有损耗的情况下的最佳行动规划，以及解决有移动目标的 "旅行推销员问题"（TSP）。我们研究的目的是通过将该问题分解为各组成部分的问题，然后提出各组成部分的概念验证方案来分析该问题。这篇论文的主要成果包括一个建模框架，在这个框架中，可以在不需要约束的情况下进行优化；比较使用不同类型的成本函数进行优化的优势（例如，最小化高价值单位被摧毁的机会与基于防御者相对于攻击者的路径的度量）；以及通过将其映射到标准TSP或使用机器学习来解决某些限制下的移动目标TSP。

1.1 战斗中的自主系统

自动化系统，特别是无人驾驶飞行器（UAVs）的迅速增加，改变了现代战场。美国已经率先在整个作战范围内开发和实施无人机，从信号情报到无人机精确打击[1], [2]。然而，我们的对手继续取得有意义的进展，最近的例子是俄罗斯在乌克兰使用中国制造的无人机[3]，无人机可能参与了最近对北溪管道的破坏[4]，甚至恐怖组织的小规模、低技术的无人机攻击[5]。

美国继续按照无人驾驶航空系统（UAS）路线图[6], [7]发展其无人机能力，该路线图规定了无人机平台的几个重要任务，包括情报、监视和侦察（ISR）、压制敌方防空（SEAD）、电子攻击、网络节点/通信中继和空中投递/补给。然而，这份清单中明显缺少的是无人机系统的防御。无人机战争的一个新的和发展中的方面，即无人机对无人机的交战，迫在眉睫。有许多无人机防御系统正在开发中，包括地面激光系统，如海军陆战队的紧凑型激光武器系统（CLWS）[8]和导弹系统，如陆军的KuRFS和Coyote Effectors[9]。然而，新的反无人机系统（C-UAS）无人机正在开发中，如洛克希德-马丁公司的MORFIUS[10]，它使用高功率微波（HPM）武器系统，使敌方无人机在飞行中失效。

美国军方和国防部（DOD）总体上对其无人机能力进行了大量投资，这不仅包括人员、设备和武器，还包括对无人机和蜂群的战术运用的大量研究，而这些研究超出了最近取得巨大成功的ISR和精确打击能力[11], [12]。在2019年的指挥官规划指南中，海军陆战队指挥官大卫-H-伯杰将军要求建立一个 "适合侦察、监视和提供致命和非致命效果的强大的无人系统家族"，以及 "大大增加我们在其他领域成熟无人驾驶能力的努力" [13]。正是在这些其他领域，我们必须继续创新，特别是在我们对抗对手在无人机/无人机系统开发方面的成果的能力方面。

2021年，美国防部发布了其C-UAS战略，确定了其核心挑战：小型无人机系统（sUAS）的指数级增长给美国防部带来了新的风险。技术趋势正在极大地改变小型无人机系统的合法应用，同时使它们成为国家行为者、非国家行为者和犯罪分子手中日益强大的武器。当被疏忽或鲁莽的操作者控制时，小型无人机系统也可能对国防部在空中、陆地和海洋领域的行动构成危害。国防部必须在越来越多的小型无人机系统与国防部飞机共享天空、在国防部设施上空运行以及被我们国家的对手使用的环境中，保护和捍卫人员、设施和资产[14]。

虽然该战略要求在理论、组织、训练、物资、领导和教育、人员、设施-政策（DOTMLPF-P）等方面应对这些挑战，但必须做更多的工作，将研究/开发与战术层面的使用结合起来，并使之同步。这篇论文的目的就是要弥补这些领域之间的差距。

1.2 目前的工作

为了提高ISR能力，无人机技术早期发展的大部分学术工作都致力于各种学科的最佳路径控制，但具体的军事应用包括为ISR任务避免碰撞/雷达[15]。这项工作的成功从美国的无人机精确打击能力中可见一斑。在海军研究生院（NPS），Kaminer等人就大型蜂群的动力学和行为开展了大量的工作[16]-[20]。尽管有很长的工作历史，这些最近的论文提出了高价值单位防御中的一个新的最佳控制问题，开发了具有损耗建模的最佳控制问题的计算框架，并开发了高效的数值框架来解决最佳控制问题中的不确定参数

许多文献都涉及到减员模型。兰彻斯特损耗模型使用微分方程来研究敌对部队的依赖性损耗，自第一次世界大战（WWI）以来，该模型被有力地运用于战斗研究[21], [22]。一些工作已经确定了需要并解决了明确结合最优控制和损耗建模的问题[23], [24]。然而，并不存在将这些领域有效地结合在一起的一般框架或理论，当它们被解决时，其结果往往是高度特定的场景。

本论文的大部分内容将关注旅行销售员问题（TSP）在动态环境中的应用。最佳控制和TSP在物理学和工程科学中经常有交集。例如，一个这样的问题可能是由航天器以最佳方式访问木星的所有79颗卫星[25]。Moraes和Freitas通过比较几种启发式算法来解决移动目标TSP（MT-TSP），并应用于人群和无人机检测[26]。

1.3 开放式问题

耦合兰彻斯特损耗模型、最优控制理论和TSP的问题对于大领域的超级蜂群是难以解决的。然而，无人机防御研究必须关注这三个领域的交叉点，以便适当地解决这一领域现存的军事战术和战略问题。超级蜂群系统的基本特征还没有得到很好的理解，尽管随着我们扩大小型蜂群参与战略和框架的规模，它们的属性可能会出现。

图 1.1 一般研究问题的解决框图

本论文从这个有利的角度来探讨这个问题，从小型蜂群开始，开发新的方法来解决更多可解决的系统，然后可以扩大规模。

每一种方法都考虑到sUAS有限的机载计算能力和作战期间有限的可用时间。如图1.1和1.2所概述的一般研究问题，首先是估计诸如武器类型、武器效能、无人机群类型等参数。本论文将把所有的参数视为常量、已知量。关于参数的不确定性分析见Walton等人[17]。

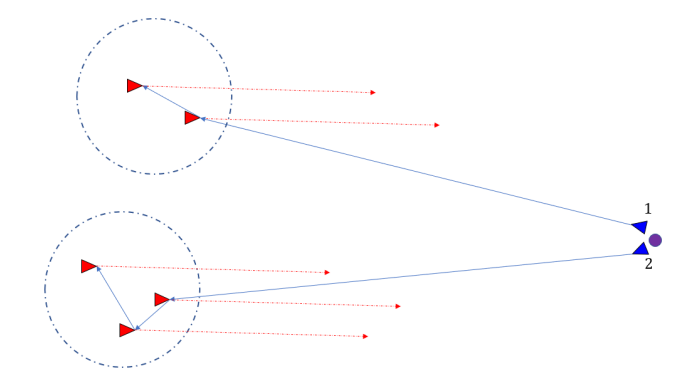
图1.2 研究问题的场景可视化

其次，一群防御性无人机必须决定如何分割即将到来的攻击者集合，以便以最佳方式与他们交战，使高价值单位（HVU）的生存概率最大化。本论文将这一场景限制在单一防御无人机上。关于多重TSP（MTSP），见参考文献[27]-[29]。

1.4 提纲

剩下的几块，决定攻击顺序和路径优化，将在下面几章讨论。第二章假设已经知道或选择了合理的攻击顺序，并解决相关的科学问题，即如何使HVU的生存率最大化。我们偏离了最优控制的路径优化，而是致力于建立全新的、无约束的优化框架的可行性，在这里我们讨论了各种成本函数的优点和缺点。第三章和第四章分别从TSP和机器学习（ML）的有利角度解决攻击顺序问题。

第三章试图消除MT-TSP的时间依赖性，以证明动态版本的TSP仍然可以在转换的空间上采用传统的TSP算法，第四章为ML的应用建立了一个概念证明。最后，第五章展示了我们开发的图形用户界面（GUI）的功能，作为无人机防御任务规划的辅助工具。