《对抗性几何规划研究》2022最新论文，捷克理工大学

人工智能的主要目标之一是构建智能Agent，如计算机游戏中的对手或将包裹送到客户手中的无人驾驶飞行器。这些智能Agent在各种环境中感知和行动以实现其目标。例如，在电脑游戏的情况下，目标是击败玩家。在包裹运送无人机的情况下，目标是将包裹及时送到客户手中。

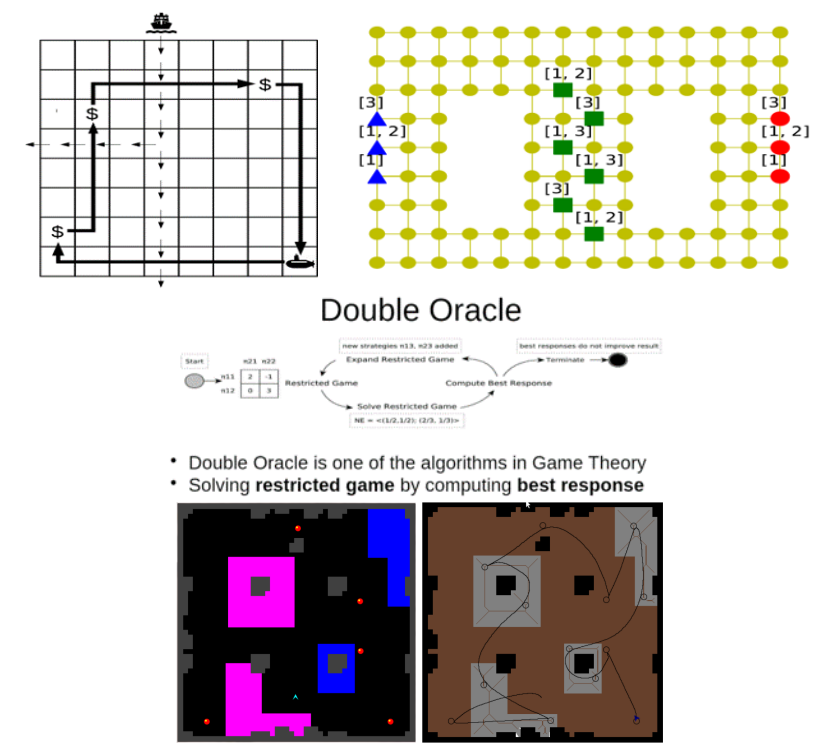
Agent感知环境的状态，并需要决定下一步该做什么。一种可能的方法是强化学习[36]，即Agent从与环境的互动中学习。这种方法在一些领域是成功的，在围棋[60]、《星际争霸》[66]或Atari游戏[41]中取得了超人的表现。Agent如何在环境中行动的另一种方法是事先创建一个行动计划。对于一个给定的目标，Agent计算出导致它的行动序列。自动计划在许多领域都是成功的，如深空1号[4]或火星探测器任务[1]。自动规划的一个缺点是，当环境意外改变时，Agent通常不能再向目标前进。这种情况要么是随机发生的，要么是由其他对手Agent的行动引起的。为了明确地推理其他Agent并找到一个稳健的计划，必须使用博弈论方法[59]，如 double-oracle（DO，见图1）。博弈论算法在实践中有几个成功的应用，例如，在物理安全[64]或保护野生动物[19]领域。我们关注的更多案例是战斗情况，如用无人机保卫核电站，抵御侵略者。

这项工作的主要目标是通过加强几何推理来推进自动对抗性规划的算法。尽管规划域定义语言（PDDL）[39]是一个富有表现力的建模工具，但对行动的结构有一个重要的限制：行动的参数被限制在有限（实际上是明确列举的）域的值上。这种限制的动机是，它确保了有基础的行动集合是有限的，而且，忽略持续时间，在一个状态下的行动选择的分支因素也是有限的。尽管持续时间参数可以使这种选择无限大，但很少有规划者支持这种可能性，而是将自己限制在固定的持续时间上。像吉普车穿越未知宽度的沙漠这样的问题是无法解决的[32]。

图 1：对抗性规划、资源分配、双预言机算法、几何导航（从左到右）。

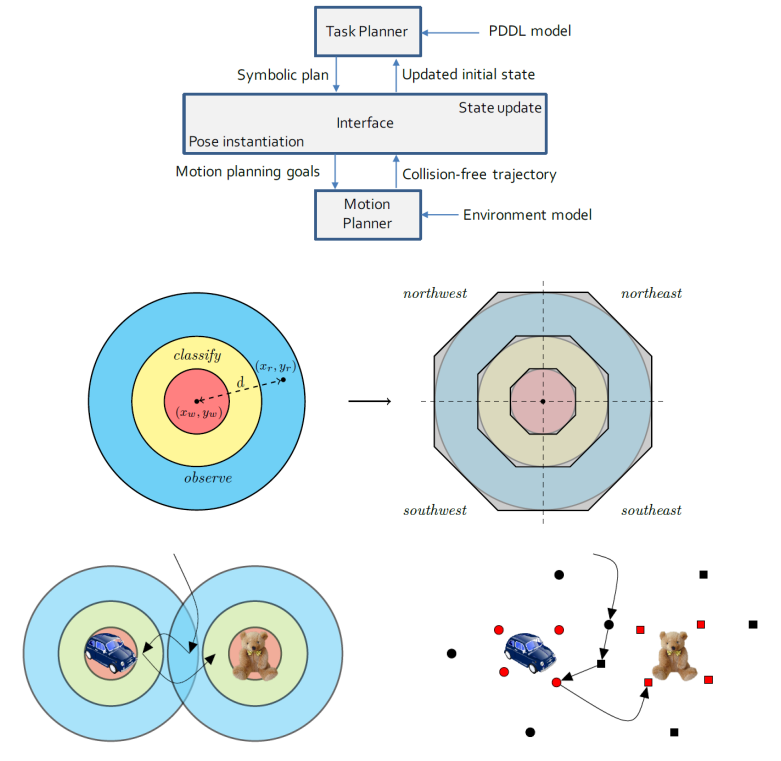
我们提议对PDDL进行扩展，以丰富具有几何特征的行动。我们实现了能够将推理提升到空间领域的规划器，并将其应用于对抗性环境。我们说明这些方法可以解决有趣的问题，并将这项工作应用于任务和运动规划场景（图2），以表明我们的工作有很大的潜力，可以重新发明机器人技术中使用任务规划器的方式。即使没有对手，几何学也是有效的，但在DO算法中，规划器被多次调用以获得最佳响应，所以作为一个乘数，我们有，如果对手的规划域是几何学的，可溶性和扩展性会变得更好。

图 2：几何任务-运动规划：循环、线性近似、检查运动规划（从左到右）。